12  Die Atome des Kausalität

12.1 Lernsteuerung

12.1.1 Position im Modulverlauf

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

12.1.2 R-Pakete

Für dieses Kapitel benötigen Sie folgende R-Pakete:

library(tidyverse)
library(rstanarm)
library(easystats)

12.1.3 Daten

Wir nutzen den Datensatz Saratoga County; s. Tabelle 11.3. Hier gibt es eine Beschreibung des Datensatzes.

Sie können ihn entweder über die Webseite herunterladen:

SaratogaHouses_path <- "https://vincentarelbundock.github.io/Rdatasets/csv/mosaicData/SaratogaHouses.csv"

d <- read.csv(SaratogaHouses_path)

Oder aber über das Paket mosaic importieren:

data("SaratogaHouses", package = "mosaicData")
d <- SaratogaHouses  # kürzerer Name, das ist leichter zu tippen

12.1.4 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können …

• erklären, wann eine Kausalaussage gegeben eines DAGs berechtigt ist
• erklären, warum ein statistisches Modell ohne Kausalmodell zumeist keine Kausalaussagen treffen kann
• die “Atome” der Kausalität eines DAGs benennen
• “kausale Hintertüren” schließen

12.1.5 Begleitliteratur

Dieses Kapitel vermittelt die Grundlagen der Kausalinferenz mittels graphischer Modelle. Ähnliche Darstellungen wie in diesem Kapitel findet sich bei Rohrer (2018).

12.2 Kollision

📺 Kollision

12.2.1 Kein Zusammenhang von Intelligenz und Schönheit (?)

Gott ist gerecht (?)

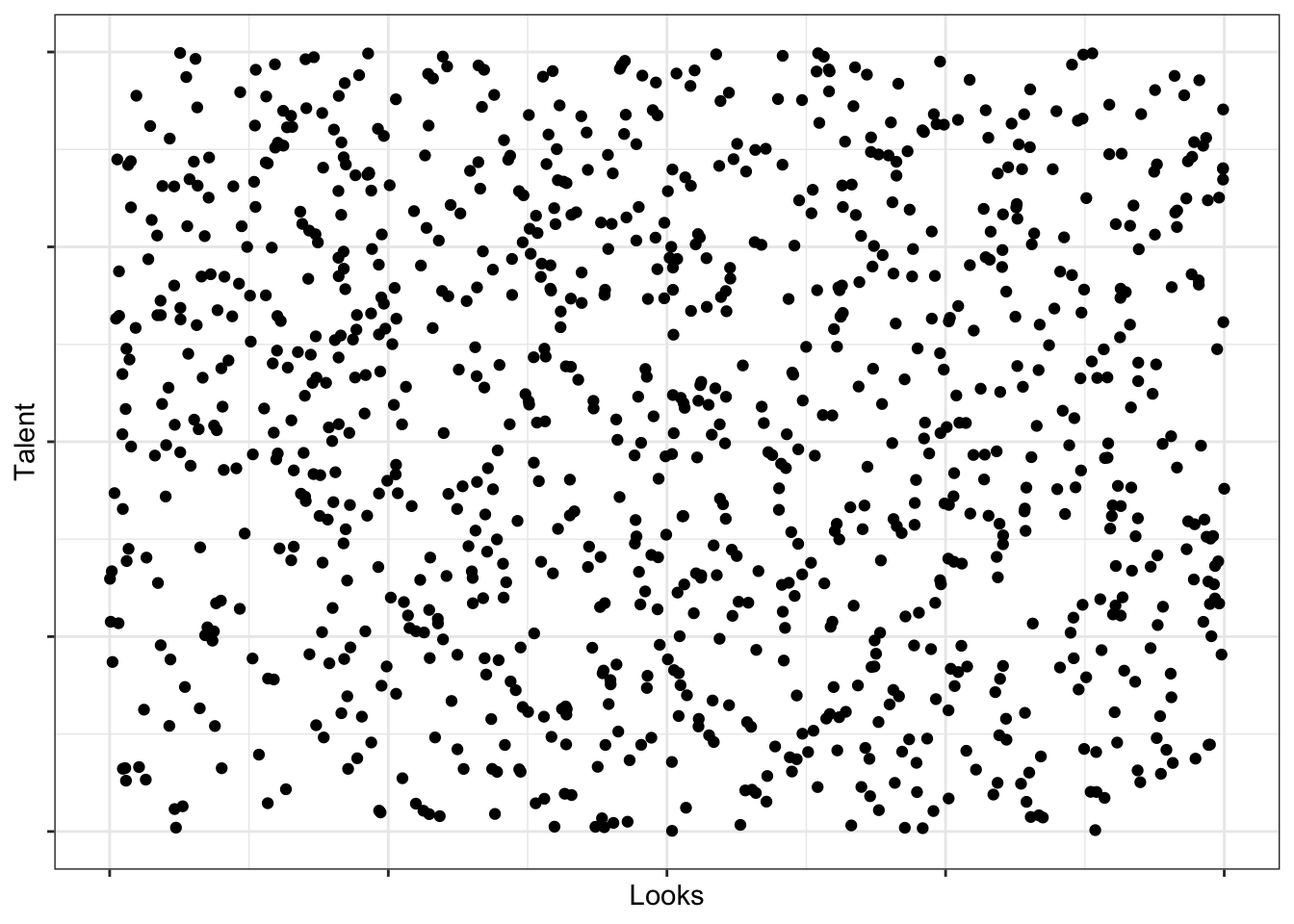
Zumindest findet sich in folgenden Daten kein Zusammenhang von Intelligenz (talent) und Schönheit (looks), wie Abbildung 12.1 illustriert. Für geringe Intelligenzwerte gibt es eine breites Spektrum von Schönheitswerten und für hohe Intelligenzwerte sieht es genauso aus.

Abbildung 12.1: Kein Zusammenhang von Intelligenz und Schönheit in den Daten

12.2.2 Aber Ihre Dates sind entweder schlau oder schön

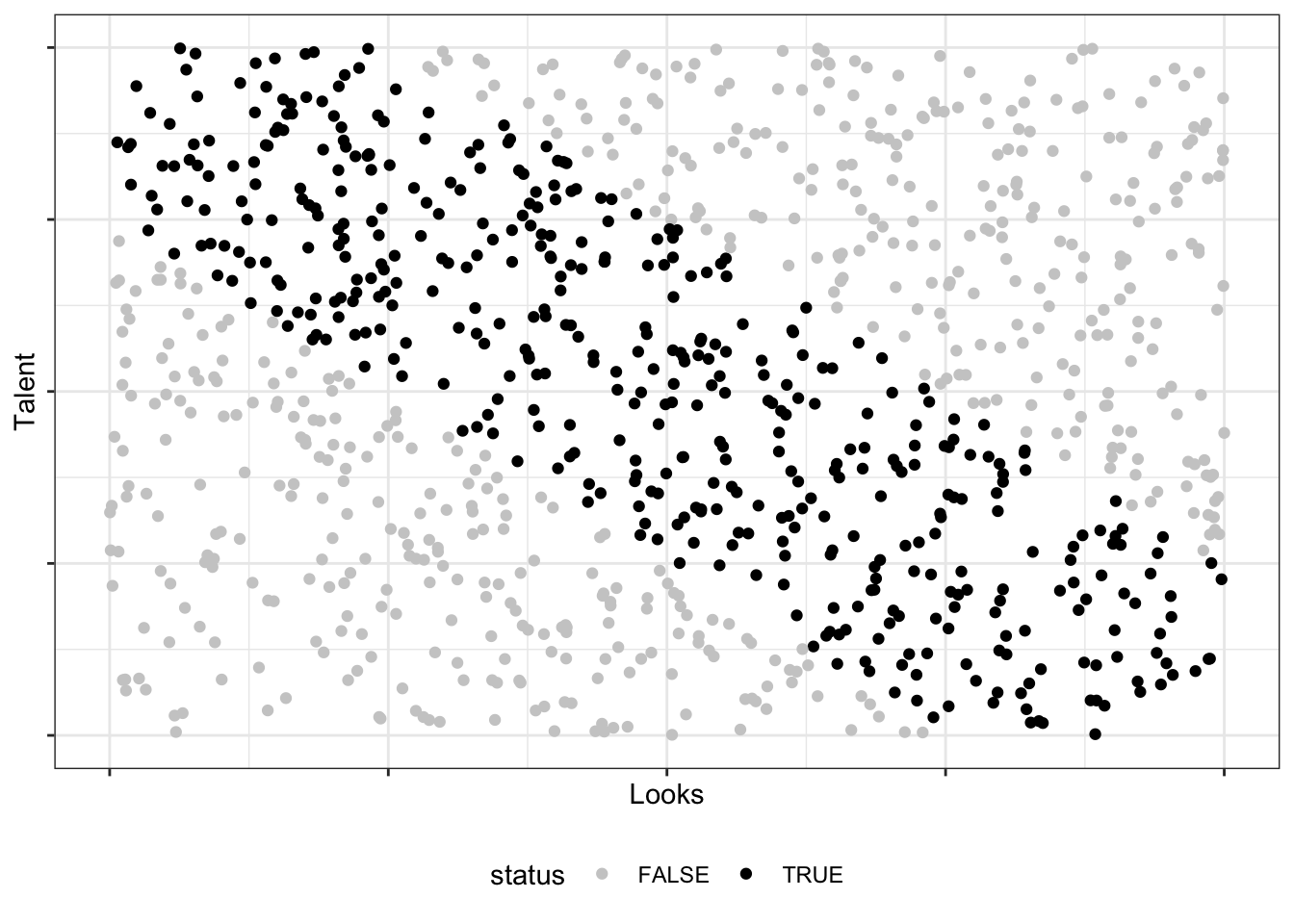
Seltsamerweise beobachten Sie, dass die Menschen, die Sie daten (Ihre Dates), entweder schön sind oder schlau - aber seltens beides gleichzeitig (schade), s. Abbildung 12.2.

Abbildung 12.2: Ihre Datingpartner sind komischerweise entweder schlau oder schön (aber nicht beides), zumindest in der Tendenz.

Wie kann das sein?

12.2.3 DAG zur Rettung

🦹 🦸

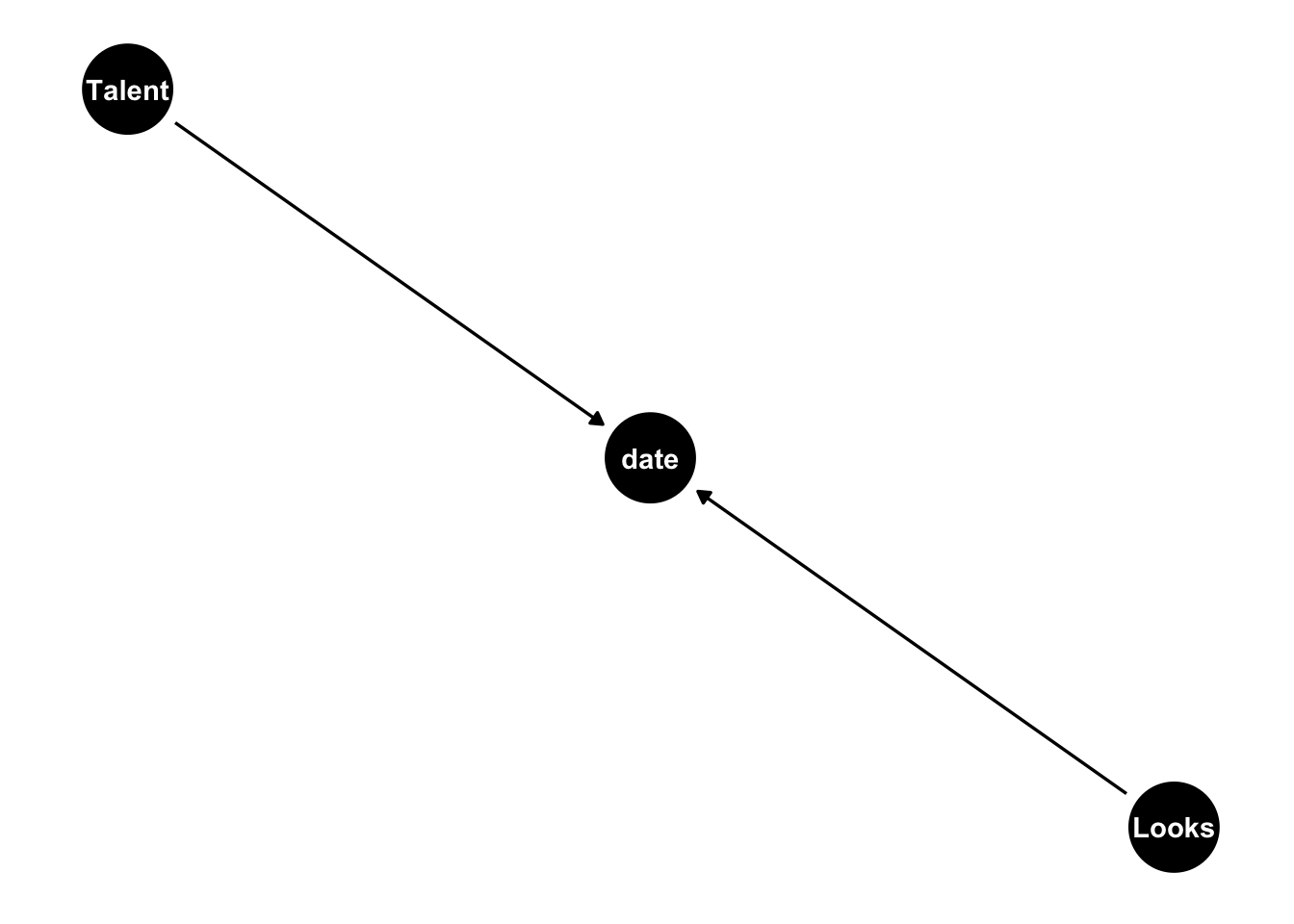
Der DAG in Abbildung 12.3 bietet eine rettende Erklärung.

Abbildung 12.3: Date als gemeinsame Wirkung von Schönheit und Intelligenz. Stratifiziert man die gemeinsame Wirkung (dates), so kommt es zu einer Scheinkorrelation zwischen Schönheit und Intelligenz.

Eine ähnliche Visualisierung des gleichen Sachverhalts zeigt Abbildung 12.4.

Abbildung 12.4: Durch Kontrolle der gemeinsamen Wirkung entsteht eine Scheinkorrelation zwischen den Ursachen

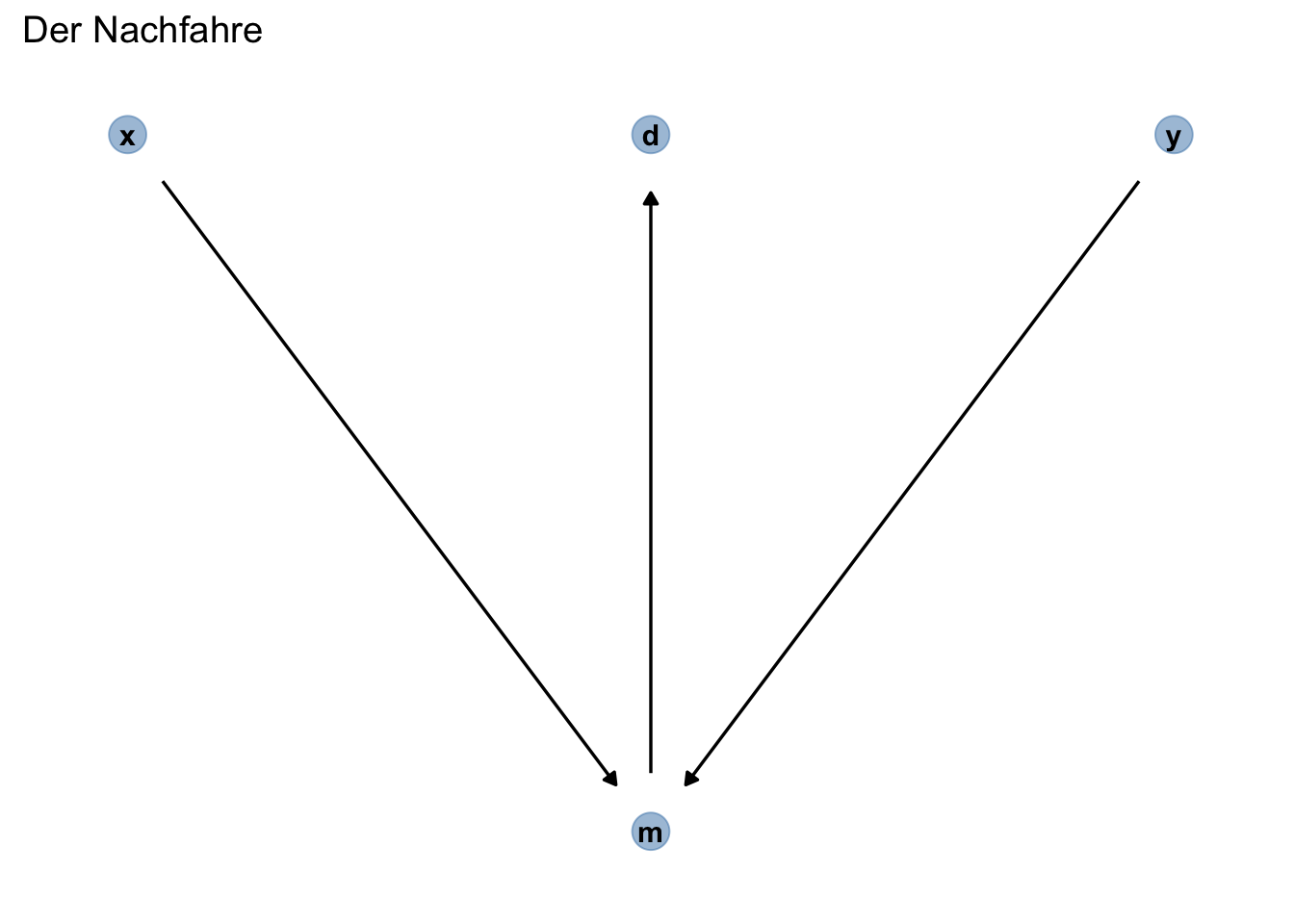
12.2.4 Was ist eine Kollision?

Definition 12.1 (Kollision) Als Kollision (Kollisionsverzerrung, Auswahlverzerrung, engl. collider) bezeichnet man einen DAG, bei dem eine Wirkung zwei Ursachen hat (eine gemeinsame Wirkung zweier Ursachen) (Pearl et al., 2016, p. 40). \(\square\)

Kontrolliert man die Wirkung m, so entsteht eine Scheinkorrelation zwischen den Ursachen x und y. Kontrolliert man die Wirkung nicht, so entsteht keine Scheinkorrelation zwischen den Ursachen, s. Abbildung 12.3, vgl. Rohrer (2018).

Wichtig

Man kann also zu viele oder falsche Prädiktoren einer Regression hinzufügen, so dass die Koeffizienten nicht die kausalen Effekte zeigen, sondern durch Scheinkorrelation verzerrte Werte.

Tipp

🙅‍♀️ Kontrollieren Sie keine Kollisionsvariablen. \(\square\)

12.2.5 Einfaches Beispiel zur Kollision

In der Zeitung Glitzer werden nur folgende Menschen gezeigt:

• Schöne Menschen 🪞
• Reiche Menschen 🤑

Sehen wir davon aus, dass Schönheit und Reichtum unabhängig voneinander sind.

Übungsaufgabe 12.1 Wenn ich Ihnen sage, dass Don nicht schön ist, aber in der Glitzer häufig auftaucht, was lernen wir dann über seine finanzielle Situation?¹ \(\square\)

“Ich bin schön, unglaublich schön, und groß, großartig, tolle Gene!!!” 🧑

12.2.6 Noch ein einfaches Beispiel zur Kollision

“So langsam check ich’s!” 🧑²

Sei Z = X + Y, wobei X und Y unabhängig sind.

Wenn ich Ihnen sage, X = 3, lernen Sie nichts über Y, da die beiden Variablen unabhängig sind Aber: Wenn ich Ihnen zuerst sage, Z = 10, und dann sage, X = 3, wissen Sie sofort, was Y ist (Y = 7).

Also: X und Y sind abhängig, gegeben Z: \(X \not\perp \!\!\! \perp Y \,|\, Z\).³

12.2.7 Durch Kontrollieren entsteht eine Verzerrung bei der Kollision

Abbildung 12.3 zeigt: Durch Kontrollieren entsteht eine Kollision, eine Scheinkorrelation zwischen den Ursachen.

Kontrollieren kann z.B. bedeuten:

• Stratifizieren: Aufteilen von date in zwei Gruppen und dann Analyse des Zusammenhangs von talent und looks in jeder Teilgruppe von date
• Kontrollieren mit Regression: Durch Aufnahme von date als Prädiktor in eine Regression zusätzlich zu looks mit talent als Prädikotr

Ohne Kontrolle von date entsteht keine Scheinkorrelation zwischen Looks und Talent. Der Pfad (“Fluss”) von Looks über date nach Talent ist blockiert.

Kontrolliert man date, so öffnet sich der Pfad Looks -> date -> talent und die Scheinkorrelation entsteht: Der Pfad ist nicht mehr “blockiert”, die Korrelation kann “fließen” - was sie hier nicht soll, denn es handelt sich um Scheinkorrelation.

Das Kontrollieren von date geht zumeist durch Bilden einer Auswahl einer Teilgruppe von sich.

12.2.8 IQ, Fleiss und Eignung fürs Studium

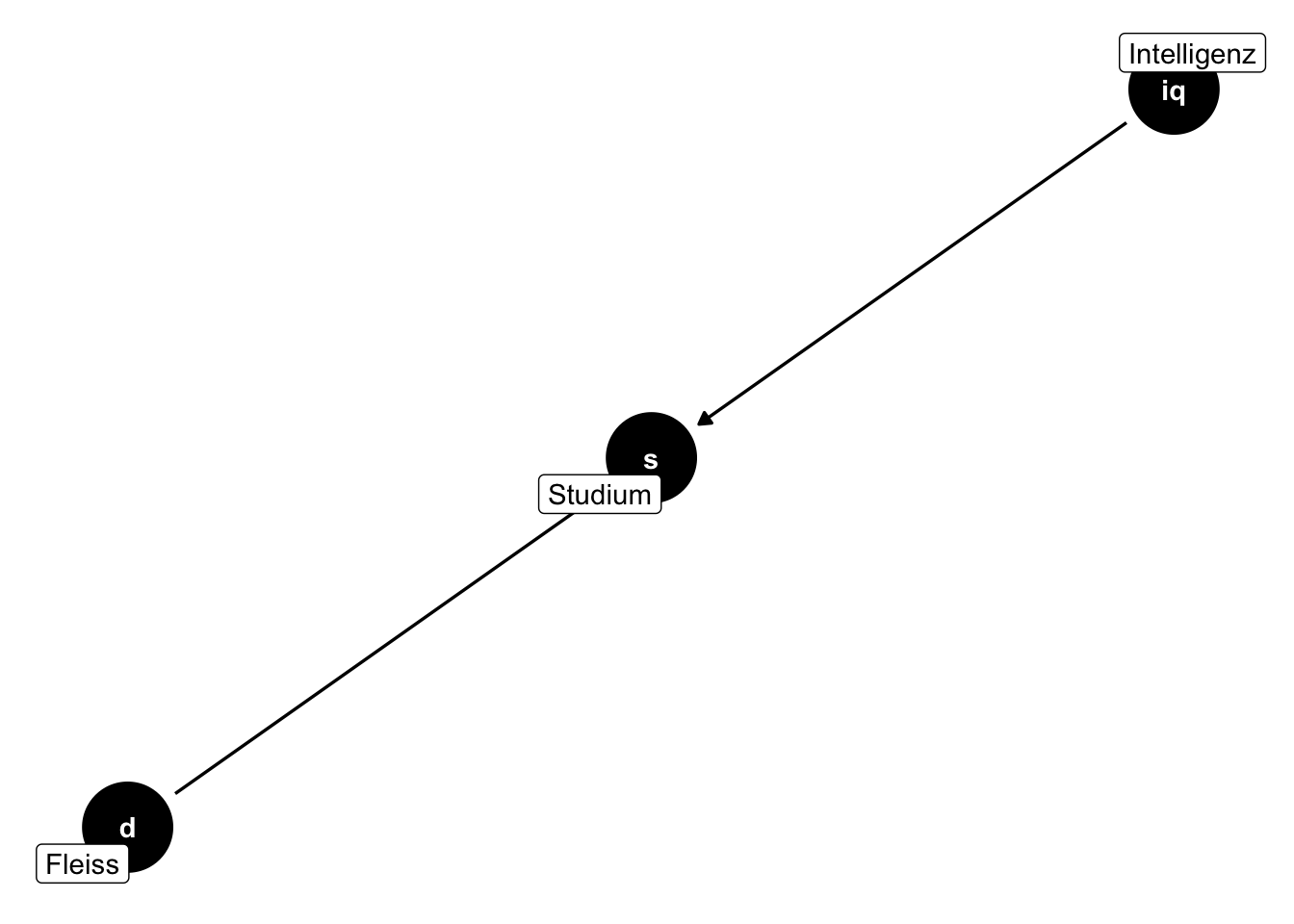
Sagen wir, über die Eignung für ein Studium würden nur (die individuellen Ausprägungen) von Intelligenz (IQ) und Fleiss entscheiden, s. den DAG in Abbildung 12.5.

Abbildung 12.5: Kollisionsstruktur im Dag zur Studiumseignung

Bei positiver eignung wird ein Studium aufgenommen (studium = 1) ansonsten nicht (studium = 0).

Quelle

eignung (fürs Studium) sei definiert als die Summe von iq und fleiss, plus etwas Glück, s. Listing 12.1.

Listing 12.1: Eignung ist die Summe von Fleiss und Intelligenz, plus ein Quentchen Glück

set.seed(42)  # Reproduzierbarkeit
N <- 1e03  

d_eignung <-
tibble(
  iq = rnorm(N),  # normalverteilt mit MW=0, sd=1
  fleiss = rnorm(N),
  glueck = rnorm(N, mean = 0, sd = .1),
  eignung = 1/2 * iq + 1/2 * fleiss + glueck,
  # nur wer geeignet ist, studiert (in unserem Modell):
  studium = ifelse(eignung > 0, 1, 0) 
  )

Laut unserem Modell setzt sich Eignung zur Hälfte aus Intelligenz und zur Hälfte aus Fleiss zusammen, plus etwas Glück.

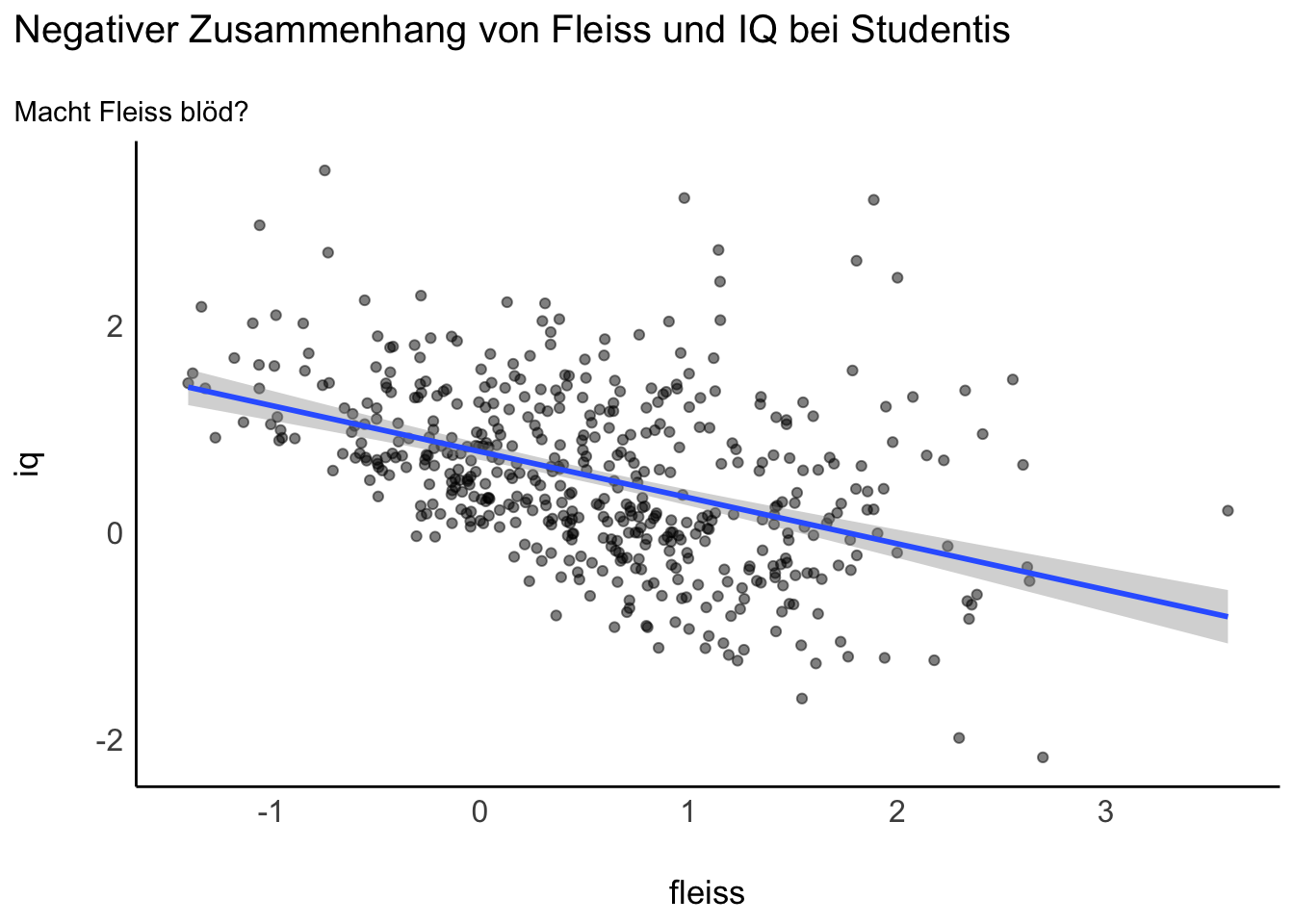
12.2.9 Schlagzeile “Fleiß macht blöd!”

Eine Studie untersucht den Zusammenhang von Intelligenz (iq) und Fleiß (f) bei Studentis (s). Ergebnis: Ein negativer Zusammenhang!?

Berechnen wir das “Eignungsmodell”, aber nur mit Studis (studium == 1, also ohne Nicht-Studis), s. Tabelle 12.1.

m_eignung <-
  stan_glm(iq ~ fleiss, data = d_eignung %>%  filter(studium == 1), refresh = 0)

hdi(m_eignung)

Tabelle 12.1: Zum Zusammenhang von Fleiss und Talent

Highest Density Interval

Parameter	95% HDI
(Intercept)	[ 0.70, 0.86]
fleiss	[-0.53, -0.36]

Abbildung 12.6 zeigt das Modell und die Daten.

Abbildung 12.6: Der Zusammenhang von Fleiss und IQ

IQ ist nicht unabhängig von Fleiß in unseren Daten, sondern abhängig. Nichtwissenschaftliche Berichte, etwa in einigen Medien, greifen gerne Befunde über Zusammenhänge auf und interpretieren die Zusammenhänge – oft vorschnell – als kausal.⁴

12.2.10 Kollisionsverzerrung nur bei Stratifizierung

Definition 12.2 (Stratifizieren) Durch Stratifizieren wird eine Stichprobe in (homogene) Untergruppen unterteilt (sog. Strata). \(\square\)

Nur durch das Stratifizieren (Aufteilen in Subgruppen, Kontrollieren, Adjustieren) tritt die Scheinkorrelation auf, s. Abbildung 12.7.

Hinweis

Ohne Stratifizierung tritt keine Scheinkorrelation auf. Mit Stratifizierung tritt Scheinkorrelation auf.

Abbildung 12.7: Stratifizierung und Scheinkorrelation. A: Keine Stratifizierung und keine Scheinkorrelation. B: Stratifizierung und Scheinkorrelation

Wildes Kontrollieren einer Variablen - Aufnehmen in die Regression - kann genausog ut schaden wie nützen.

Nur Kenntnis des DAGs verrät die richtige Entscheidung: ob man eine Variable kontrolliert oder nicht.

Hinweis

Nimmt man eine Variable als zweiten Prädiktor auf, so “kontrolliert” man diese Variable. Das Regressiongewicht des ersten Prädiktors wird “bereinigt” um den Einfluss des zweiten Prädiktors; insofern ist der zweite Prädiktor dann “kontrolliert”.

12.2.11 Einfluss von Großeltern und Eltern auf Kinder

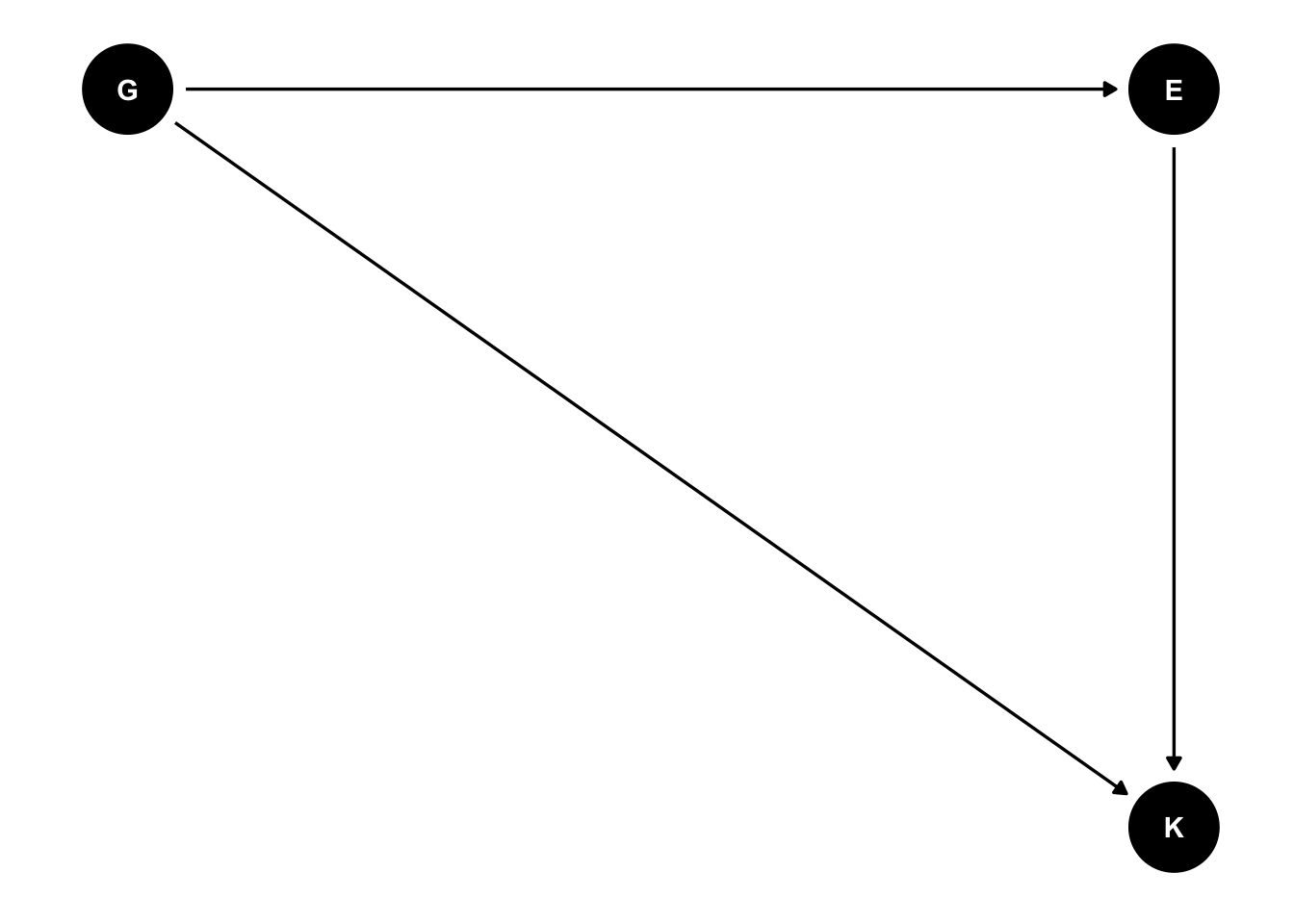
Wir wollen hier den (kausalen) Einfluss der Eltern E und Großeltern G auf den Bildungserfolg der Kinder K untersuchen.

Wir nehmen folgende Effekte an:

• indirekter Effekt von G auf K: \(G \rightarrow E \rightarrow K\)
• direkter Effekt von E auf K: \(E \rightarrow K\)
• direkter Effekt von G auf K: \(G \rightarrow K\)

Wir sind v.a. interessiert an \(G \rightarrow K\), dem direkten kausalen Effekt von Großeltern auf ihre Enkel, s. Abbildung 12.8, \(G \rightarrow K\).

Abbildung 12.8: Der kausale Effekt von Großeltern auf Enkel. Ein verlorener Fall, zumindest was den DAG betrifft

Aber was ist, wenn wir vielleicht eine unbekannte Variable übersehen haben? (S. nächster Abschnitt). 👻

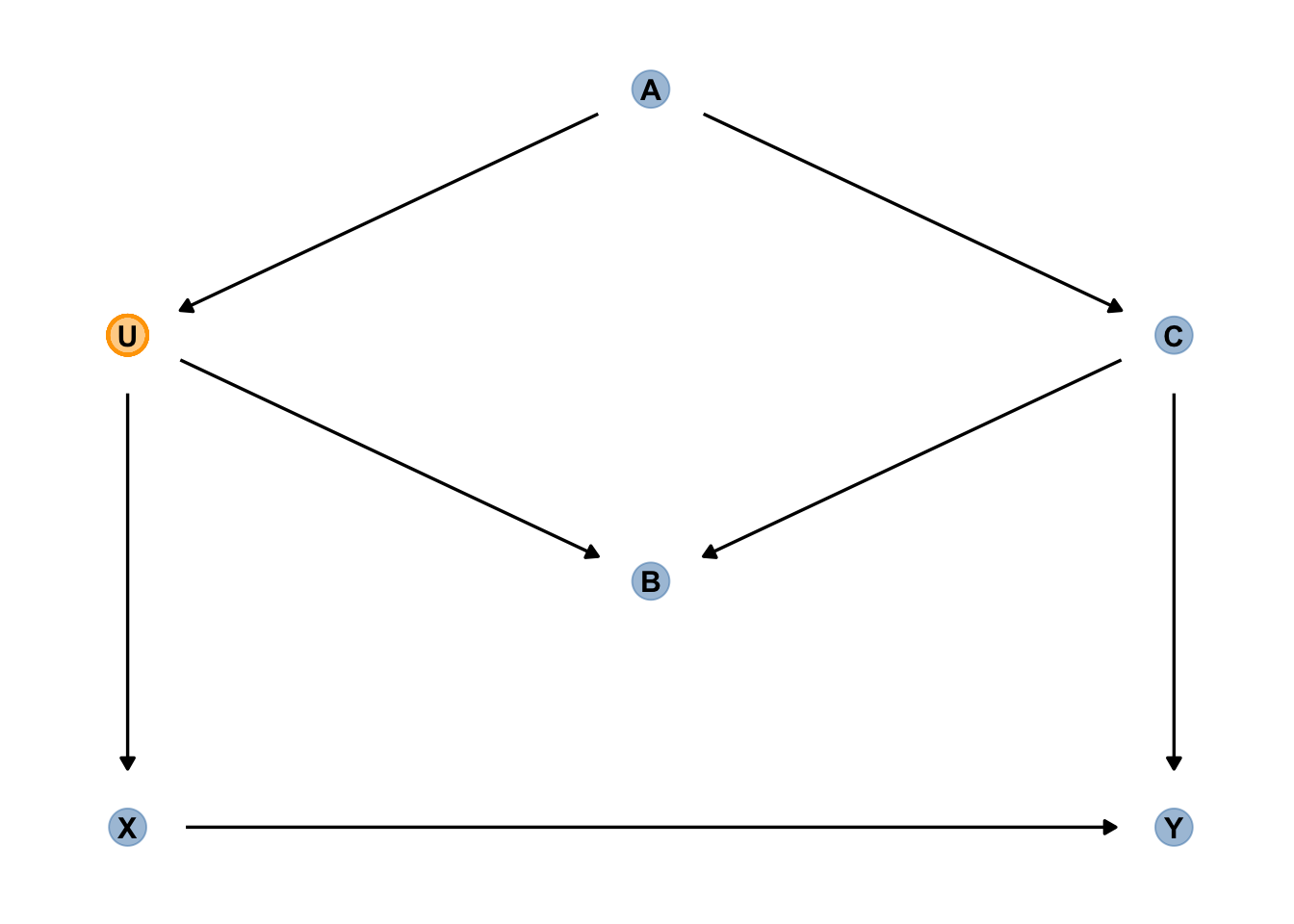
12.2.12 Der Gespenster-DAG

👻 Es gibt “unheilbare” DAGs, nennen wir sie “Gespenster-DAGs”, in denen es nicht möglich ist, einen (unverzerrten) Kausaleffekt zu bestimmen, s. Abbildung 12.9. Letztlich sagt uns der DAG bzw. unsere Analyse zum DAG: “Deine Theorie ist nicht gut, zurück an den Schreibtisch und denk noch mal gut nach. Oder sammele mehr Daten.”

Abbildung 12.9: Der Gespenster-DAG: Eine Identifikation der Kausaleffekt ist nicht (vollständig) möglich.

U könnte ein ungemessener Einfluss sein, der auf E und K wirkt, etwa Nachbarschaft. Die Großeltern wohnen woanders (in Spanien), daher wirkt die Nachbarschaft der Eltern und Kinder nicht auf sie. E ist sowohl für G als auch für U eine Wirkung, also eine Kollisionsvariable auf diesem Pfad. Wenn wir E kontrollieren, wird es den Pfad \(G \rightarrow K\) verzerren, auch wenn wir niemals U messen.

Die Sache ist in diesem Fall chancenlos. Wir müssen diesen DAG verloren geben, McElreath (2020), S. 180; ein Gespenster-DAG. 👻

12.3 Die Hintertür schließen

Definition 12.3 (Hintertür) Eine “Hintertür” ist ein nicht-kausaler Pfad zwischen einer UV und einer AV. Ein Hintertürpfad entsteht, wenn es eine alternative Route über eine oder mehrere Variable gibt, die UV mit der AV verbindet. Dieser Pfad verzerrt die Schätzwerte des kausalen Einflusses, wenn er nicht kontrolliert wird. \(\square\)

12.3.1 Zur Erinnerung: Konfundierung

Forschungsfrage: Wie groß ist der (kausale) Einfluss der Schlafzimmerzahl auf den Verkaufspreis des Hauses?

a: livingArea, b: bedrooms, p: prize

UV: b, AV: p

Das Kausalmodell ist in Abbildung 12.10 dargestellt.

Abbildung 12.10: Der Preis wird sowohl von der Zimmerzahl als auch der Wohnfläche beeinflusst

Im Regressionsmodell p ~ b wird der kausale Effekt verzerrt sein durch die Konfundierung mit a. Der Grund für die Konfundierung sind die zwei Pfade zwischen b und p:

1. \(b \rightarrow p\)
2. \(b \leftarrow a \rightarrow p\)

Beide Pfade erzeugen (statistische) Assoziation zwischen b und p. Aber nur der erste Pfad ist kausal; der zweite ist nichtkausal. Gäbe es nur nur den zweiten Pfad und wir würden b ändern, so würde sich p nicht ändern.

12.3.2 Gute Experimente zeigen den echten kausalen Effekt

Abbildung 12.11 zeigt eine erfreuliche Situation: Die “Hintertür” zu unserer UV (Zimmerzahl) ist geschlossen!

Ist die Hintertür geschlossen - führen also keine Pfeile in unserer UV - so kann eine Konfundierung ausgeschlossen werden.

Abbildung 12.11: Unverzerrte Schätzung des kausalen Effekts unserer UV (Zimmerzahl). Das Regressionsgewicht ist hier der unverzerrte Kausaleffekt. Es spielt keine Rolle, ob der andere Prädiktor im Modell enthalten ist. Da die beiden Prädiktoren unkorreliert sind, hat die Aufnahme des einen Prädiktors keinen Einfluss auf das Regressionsgewicht des anderen.

Die “Hintertür” der UV (b) ist jetzt zu! Der einzig verbleibende, erste Pfad ist der kausale Pfad und die Assoziation zwischen b und p ist jetzt komplett kausal.

Eine berühmte Lösung, den kausalen Pfad zu isolieren, ist ein (randomisiertes, kontrolliertes⁵) Experiment. Wenn wir den Häusern zufällig (randomisiert) eine Anzahl von Schlafzimmern (b) zuweisen könnten (unabhängig von ihrer Quadratmeterzahl, a), würde sich der Graph so ändern. Das Experiment entfernt den Einfluss von a auf b. Wenn wir selber die Werte von b einstellen im Rahmen des Experiments, so kann a keine Wirkung auf b haben. Damit wird der zweite Pfad, \(b \leftarrow a \rightarrow p\) geschlossen (“blockiert”).

Wichtig

Die Stärke von (gut gemachten) Experimente ist, dass sie kausale Hintertüren schließen. Damit erlauben sie (korrekte) Kausalaussagen. \(\square\)

12.3.3 Hintertür schließen auch ohne Experimente

Konfundierende Pfade zu blockieren zwischen der UV und der AV nennt man auch die Hintertür schließen (backdoor criterion). Wir wollen die Hintertüre schließen, da wir sonst nicht den wahren, kausalen Effekt bestimmen können.

Zum Glück gibt es neben Experimenten noch andere Wege, die Hintertür zu schließen, wie die Konfundierungsvariable a in eine Regression mit aufzunehmen.

Tipp

Kontrollieren Sie Konfundierer, um kausale Hintertüren zu schließen. \(\square\)

Warum blockt das Kontrollieren von aden Pfad \(b \leftarrow a \rightarrow p\)? Stellen Sie sich den Pfad als eigenen Modell vor. Sobald Sie a kennen, bringt Ihnen Kenntnis über b kein zusätzliches Wissen über p. Wissen Sie hingegen nichts über a, lernen Sie bei Kenntnis von b auch etwas über p. Konditionieren ist wie “gegeben, dass Sie a schon kennen…”.

\(b \perp \!\!\! \perp p \,|\,a\)

12.4 Die vier Atome der Kausalanalyse

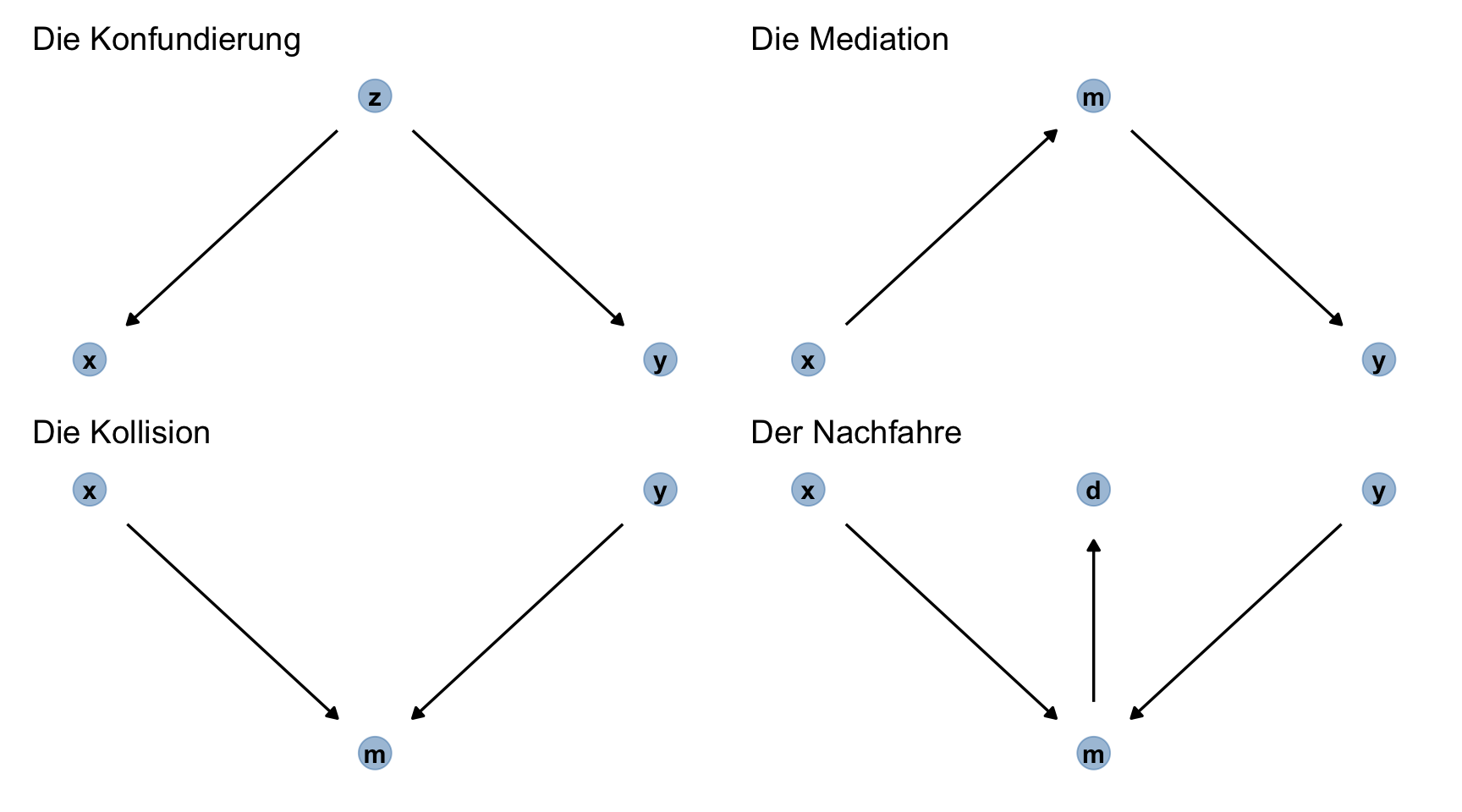
Abbildung 12.12 stellt die vier “Atome” der Kausalinferenz dar. Mehr gibt es nicht! Kennen Sie diese vier Grundbausteine, so können Sie jedes beliebige Kausalsystem (DAG) entschlüsseln.

Abbildung 12.12: Die vier Atome der Kausalinferenz

12.4.1 Mediation

Definition 12.4 (Mediator) Einen Pfad mit drei Knoten (Variablen), die über insgesamt zwei Kanten verbunden sind, wobei die Pfeile von UV zu Mediator und von Mediator zur AV zeigen, nennt man Mediation. Der Mediator ist die Variable zwischen UV und AV [Pearl et al. (2016); p. 38]. \(\square\)

Die Mediation (synonym: Wirkkette, Rohr, Kette, chain) beschreibt Pfade, in der die Kanten (eines Pfades) die gleiche Wirkrichtung haben: \(x \rightarrow m \rightarrow y\). Anders gesagt: Eine Mediation ist eine Kausalabfolge der Art \(x \rightarrow m \rightarrow y\), s. Abbildung 12.13. Die Variable in der Mitte \(m\) der Kette wird auch Mediator genannt, weil sei die Wirkung von X auf Y “vermittelt” oder überträgt. Die Erforschung von Mediation spielt eine recht wichtige Rolle in einigen Wissenschaften, wie der Psychologie.

Abbildung 12.13: Das Kausalmodell der Mediation mit x als UV, m als Mediator und Y als AV.

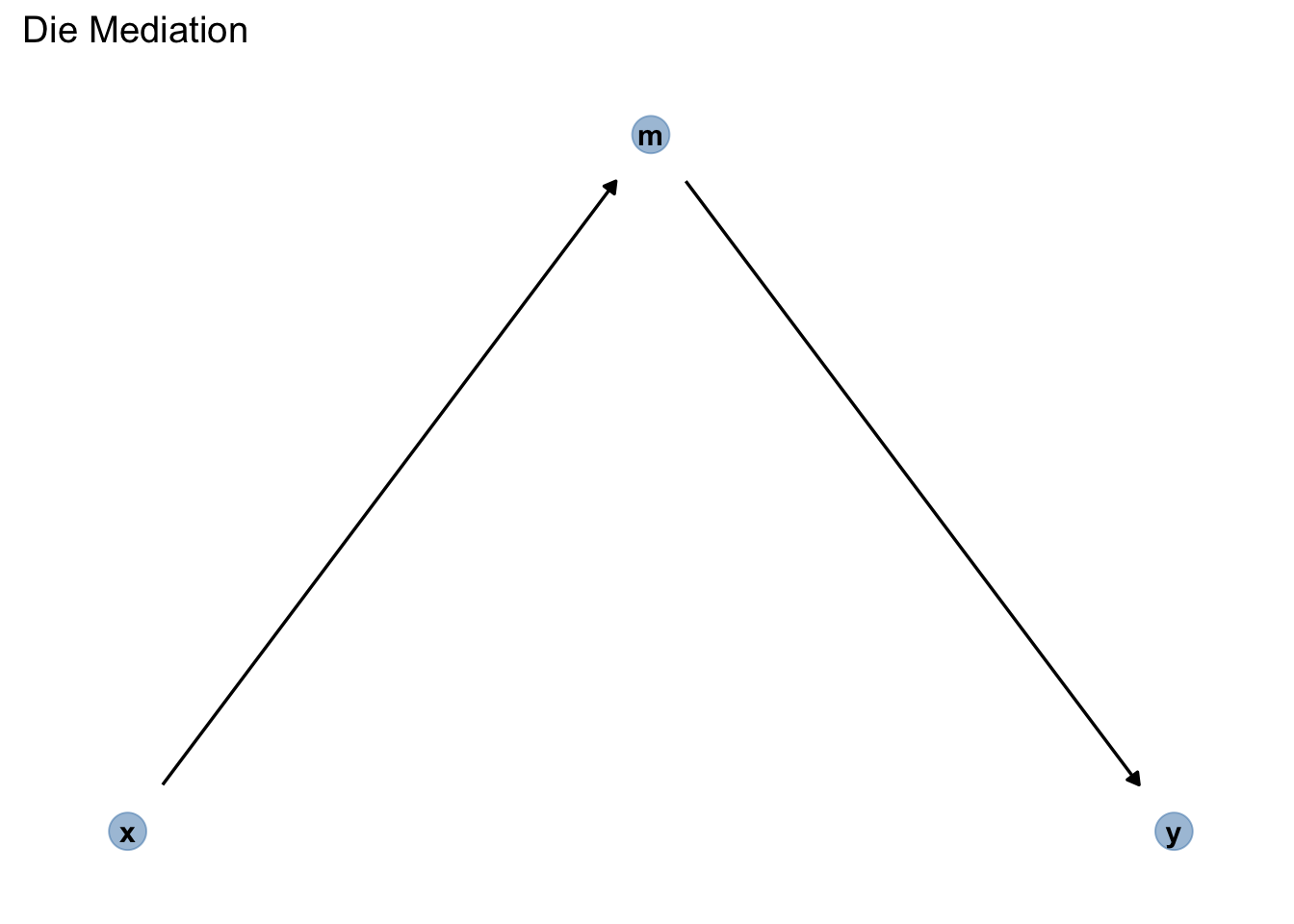
Beispiel 12.1 (Mediator kontrollieren?) Sollte man den Mediator m in Abbildung 12.13 kontrollieren, wenn man den Kausaleffekt von x auf y schätzen möchte?⁶ \(\square\)

Ohne Kontrollieren ist der Pfad offen: Die Assoziation “fließt” den Pfad entlang (in beide Richtungen). Kontrollieren blockt (schließt) die Kette (genau wie bei der Gabel).

Tipp

Kontrollieren Sie den Mediator nicht. Der Pfad über den Mediator ist ein “echter” Kausalpfad, keine Scheinkorrelation. \(\square\)

Wichtig

Das Kontrollieren eines Mediators ist ein Fehler, wenn man am gesamten (totalen) Kausaleffekt von UV zu AV interessiert ist. \(\square\)

Es kann auch angenommen werden, dass der Mediator nicht der einzige Weg von X zu Y ist, s. Abbildung 12.14. In Abbildung 12.14 gibt es zwei kausale Pfade von X zu Y: \(x\rightarrow m \rightarrow y\) und \(x \rightarrow y\).

Definition 12.5 (Effekt) Gibt es eine (von (praktisch) Null verschiedene) kausale Assoziation der UV auf die AV, so hängt die AV von der UV (kausal) ab. Man spricht von einem Effekt (der UV auf die AV). \(\square\)

Definition 12.6 (Totaler Effekt) Die Summe der Effekte aller (kausalen) Pfade von UV zu AV nennt man den totalen (kausalen) Effekt. \(\square\)

Definition 12.7 (Indirekter Effekt) Den (kausalen) Effekt über den Mediatorpfad (von \(X\) über \(M\) zu \(Y\)) nennt man den indirekten (kausalen) Effekt. \(\square\)

Definition 12.8 (Direkter Effekt) Ein Effekt, der nur aus dem Pfad \(x\rightarrow y\) besteht, also ohne keine Zwischenglieder, nennt man in Abgrenzung zum indirekten Effekt, direkten (kausalen) Effekt. \(\square\)

Abbildung 12.14: Partielle Mediation: Es gibt einen direkten Effekt (X->Y) und einen indirekten Effekt (X->M->Y).

12.4.2 Der Nachfahre

Definition 12.9 (Nachfahre) Ein Nachfahre (engl. descendent) ist eine Variable, die von einer anderen Variable beeinflusst⁷ wird, s. Abbildung 12.15. \(\square\)

Kontrolliert man einen Nachfahren d, so kontrolliert man damit zum Teil den Vorfahren (die Ursache), m. Der Grund ist, dass d Information beinhaltet über m. Hier wird das Kontrollieren von d den Pfad von x nach y teilweise öffnen, da m eine Kollisionsvariable ist.

Abbildung 12.15: Ein Nachfahre verhält sich ähnlich wie sein Vorfahre…

12.4.3 Kochrezept zur Analyse von DAGs 👨‍🍳

Wie kompliziert ein DAG auch aussehen mag, er ist immer aus diesen vier Atomen aufgebaut.

Hier ist ein Rezept, das garantiert, dass Sie welche Variablen Sie kontrollieren sollten und welche nicht: 📄

1. Listen Sie alle Pfade von UV (X) zu AV (Y) auf.
2. Beurteilen Sie jeden Pfad, ob er gerade geschlossen oder geöffnet ist.
3. Beurteilen Sie für jeden Pfad, ob er ein Hintertürpfad ist (Hintertürpfade haben einen Pfeil, der zur UV führt).
4. Wenn es geöffnete Hinterpfade gibt, prüfen Sie, welche Variablen mann kontrollieren muss, um den Pfad zu schließen (falls möglich).

12.5 Schließen Sie die Hintertür (wenn möglich)!

📺 Hintertür schließen

12.5.1 Hintertür: ja oder nein?

12.5.1.1 Fall 1: x->

\(\boxed{X \rightarrow}\)

Alle Pfade, die von der UV (X) wegführen, sind entweder “gute” Kausalpfade oder automatisch geblockte Nicht-Kausal-Pfade. In diesem Fall müssen wir nichts tun.⁸

12.5.1.2 Fall 2: ->x

\(\boxed{\rightarrow X}\)

Alle Pfade, die zur UV hinführen, sind immer Nicht-Kausal-Pfade, Hintertüren. Diese Pfade können offen sein, dann müssen wir sie schließen. Sie können auch geschlossen sein, dann müssen wir nichts tun.

Tipp

Schließen Sie immer offene Hintertüren, um Verzerrungen der Kausaleffekte zu verhinden. \(\square\)

12.5.2 bsp1

UV: \(X\), AV: \(Y\), drei Kovariaten (A, B, C) und ein ungemessene Variable, U

Abbildung 12.16: Puh, ein schon recht komplizierter DAG

Es gibt zwei Hintertürpfade in Abbildung 12.16:

1. \(X \leftarrow U \leftarrow A \rightarrow C \rightarrow Y\), offen
2. \(X \leftarrow U \rightarrow B \leftarrow C \rightarrow Y\), geschlossen

Kontrollieren von \(A\) oder (auch) \(C\) schließt die offene Hintertür.

McElreath (2020), Kurz (2021), s.S. 186.

12.5.3 Schließen Sie die Hintertür (wenn möglich)!, bsp2

S. DAG in Abbildung 12.17: UV: \(W\), AV: \(D\)

Abbildung 12.17: Welche Variablen muss man kontrollieren, um den Effekt von W auf D zu bestimmen?

Kontrollieren Sie diese Variablen, um die offenen Hintertüren zu schließen:

• entweder \(A\) und \(M\)
• oder \(S\)

Mehr Infos

Details finden sich bei McElreath (2020) oder Kurz (2021), S. 188.

12.5.4 Implizierte bedingte Unabhängigkeiten von bsp2

Auch wenn die Daten nicht sagen können, welcher DAG der richtige ist, können wir zumindest lernen, welcher DAG falsch ist. Die vom Modell implizierten bedingten Unabhängigkeiten geben uns Möglichkeiten, zu prüfen, ob wir einen DAG verwerfen (ausschließen) können. Bedingten Unabhängigkeit zwischen zwei Variablen sind Variablen, die nicht assoziiert (also stochastisch unabhängig) sind, wenn wir eine bestimmte Menge an Drittvariablen kontrollieren.

bsp2 impliziert folgende bedingte Unabhängigkeiten:

## A _||_ W | S
## D _||_ S | A, M, W
## M _||_ W | S

12.6 Fazit

12.6.1 Ausstieg

📺 Musterlösung für eine DAG-Prüfungsaufgabe

📺 Musterlösung für schwierige DAG-Prüfungsaufgaben

Beispiel 12.2 (PMI zum heutigen Stoff) Der Kreativitätsforscher Edward de Bono hat verschiedene “Denkmethoden” vorgestellt, die helfen sollen, Probleme besser zu lösen. Eine Methode ist die “PMI-Methode”. PMI steht für Plus, Minus, Interessant. Bei Plus und Minus soll man eine Bewertung von Positiven bzw. Negativen bzgl. eines Sachverhaltes anführen. Bei Interessant verzichtet man aber explizit auf eine Bewertung (im Sinne von “gut” oder “schlecht”) und fokussiert sich auf Interessantes, Überraschendes, Bemerkenswertes.

Führen Sie die PMI-Methode zum heutigen Stoff durch!

1. Plus: Was fanden Sie am heutigen Stoff gut, sinnvoll, nützlich?
2. Minus: Was finden Sie am heutigen Stoff nicht gut, sinvoll, nützlich?
3. Interessant: Was finden Sie am heutigen Stoff bemerkenswert, interessant, nachdenkenswert?

Reichen Sie die Antworten an der von der Lehrkraft angezeigten Stelle ein! \(\square\)

12.6.2 Zusammenfassung

📺 Kausalmodelle überprüfen

Wie (und sogar ob) Sie statistische Ergebnisse (z.B. eines Regressionsmodells) interpretieren können, hängt von der epistemologischen Zielrichtung der Forschungsfrage ab:

• Bei deskriptiven Forschungsfragen können die Ergebnisse (z.B. Regressionskoeffizienten) direkt interpretiert werden. Z.B. “Der Unterschied zwischen beiden Gruppen beträgt etwa …”. Allerdings ist eine kausale Interpretation nicht zulässig.
• Bei prognostischen Fragestellungen (Vorhersagen) spielen die Modellkoeffizienten keine Rolle, stattdessen geht es um vorhergesagten Werte, \(\hat{y}_i\), z.B. auf Basis der PPV. Kausalaussagen sind zwar nicht möglich, aber auch nicht von Interesse.
• Bei kausalen Forschungsfragen dürfen die Modellkoeffizienten nur auf Basis eines Kausalmodells (DAG) oder eines (gut gemachten) Experiments interpretiert werden.

Modellkoeffizienten ändern sich (oft), wenn man Prädiktoren zum Modell hinzufügt oder wegnimmt. Entgegen der verbreiteten Annahme ist es falsch, möglichst viele Prädiktoren in das Modell aufzunehmen, wenn das Ziel eine Kausalaussage ist. Kenntnis der “kausalen Atome” ist Voraussetzung zur Ableitung von Kausalschlüsse in Beobachtungsstudien.

12.6.3 Vertiefung

An weiterführender Literatur sei z.B. Cummiskey et al. (2020), Lübke et al. (2020), Pearl et al. (2016) und Dablander (2020) empfohlen. Ein gutes Lehrbuch, das auf Kausalinferenz eingeht, ist Huntington-Klein (2022). Praktischerweise ist es öffentlich lesbar. Das Web-Buch Causal Inference for the Brave and True sieht auch vielversprechend aus. Es gibt viele Literatur zu dem Thema; relevante Google-Suchterme sind z.B. “DAG”, “causal” oder “causal inference”.

12.7 Aufgaben

• Sammlung “kausal”

12.8 —

Cummiskey, K., Adams, B., Pleuss, J., Turner, D., Clark, N., & Watts, K. (2020). Causal Inference in Introductory Statistics Courses. Journal of Statistics Education, 28(1), 2–8. https://doi.org/10.1080/10691898.2020.1713936

Dablander, F. (2020). An Introduction to Causal Inference [Preprint]. PsyArXiv. https://doi.org/10.31234/osf.io/b3fkw

Huntington-Klein, N. (2022). The Effect: An Introduction to Research Design and Causality. CRC Press, Taylor & Francis Group. https://theeffectbook.net/

Kurz, S. (2021). Statistical Rethinking with Brms, Ggplot2, and the Tidyverse: Second Edition. https://bookdown.org/content/4857/

Lübke, K., Gehrke, M., Horst, J., & Szepannek, G. (2020). Why We Should Teach Causal Inference: Examples in Linear Regression with Simulated Data. Journal of Statistics Education, 1–17. https://doi.org/10.1080/10691898.2020.1752859

McElreath, R. (2020). Statistical Rethinking: A Bayesian Course with Examples in R and Stan (2. Aufl.). Taylor and Francis, CRC Press.

Pearl, J., Glymour, M., & Jewell, N. P. (2016). Causal Inference in Statistics: A Primer. Wiley.

Rohrer, J. M. (2018). Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data. Advances in Methods and Practices in Psychological Science, 1(1), 27–42. https://doi.org/10.1177/2515245917745629

---

1. Don muss reich sein.

2. Super, Don!

3. Der horizontale Balken “|” bedeutet “gegeben, dass”. Ein Beispiel lautet \(Pr(A|B)\): “Die Wahrscheinlichkeit von A, gegeben dass B der Fall ist.

4. Ehrlicherweise muss man zugeben, dass auch wissenschaftliche Berichte Daten über Zusammenhänge gerne kausal interpretieren, oft vorschnell.

5. engl. randomized, controlled trial, RCT

6. Nein, durch das Kontrollieren von m wird der Kausalpfad von x zu y geschlossen. Es kann keine kausale Assoziation von x auf y mehr “fließen”.

7. beeinflussen ist grundsätzlich kausal zu verstehen

8. Denken Sie daran, dass Sie keine Nachkommen der UV kontrollieren dürfen, da das den Kausalpfad von der UV zur AV blockieren könnte.