5  Verteilungen

Bayes:Start!

5.1 Lernsteuerung

5.1.1 Position im Modulverlauf

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

5.1.2 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können …

• die Begriffe von Wahrscheinlichkeitsdichte erläutern
• den Begriff einer Gleichverteilung erläutern
• den Begriff einer Binomialverteilung erläutern
• den Begriff einer halben Normalverteilung erläutern
• den Begriff einer Exponentialverteilung erläutern
• zentrale Konzepte in R umsetzen

5.1.3 Begleitliteratur

Der Stoff dieses Kapitels deckt sich (weitgehend) mit Bourier (2011), Kap. 6.1 und 6.3 sowie 7.1 und und 7.2.

5.1.4 Vorbereitung im Eigenstudium

Dieses Kapitel setzt einige Grundbegriffe voraus, wie im Buch Statistik1 von Sauer (2025) vorgestellt, insbesondere im Kapitel “Rahmen”. Benötigt wird auch der Begriff der Normalverteilung sowie der Begriff der Quantile.

Lesen Sie selbständig, zusätzlich zum Stoff dieses Kapitels, noch in Bourier (2011) folgende Abschnitte:

• Kap. 7.1.1 (Binomialverteilung)
• Kap. 7.2.1 (Gleichverteilung)
• Kap. 7.2.3 (Normalverteilung)

Lösen Sie auch die Übungsaufgaben dazu.

Weitere Übungsaufgaben finden Sie im dazugehörigen Übungsbuch, Bourier (2022).

5.1.5 Prüfungsrelevanter Stoff

Beachten Sie, dass neben den Inhalten des Kapitels auch stets der vorzubereitende Stoff prüfungsrelevant ist.

5.1.6 Benötigte R-Pakete

library(tidyverse)
library(ggpubr)  # für Plots

5.1.7 Begleitvideos

• Überblick zu Verteilungen
• Gleichverteilung
• Binomialverteilung

5.2 Wichtige Verteilungen

Definition 5.1 (Verteilung) Eine Wahrscheinlichkeitsverteilung (bzw. eine HÄufigkeitsverteilung) beschreibt, wie wahrscheinlich (häufig) die Ergebnisse einer Variablen sind. $◻$

Im Folgenden sind einige wichtige Verteilungen aufgeführt, die in diesem Skript (und in der Statistik und Wahrscheinlichkeitstheorie) eine zentrale Rolle spielen.

📺 Einstieg in Verteilungen

5.3 Gleichverteilung

5.3.1 Indifferenz als Grundlage

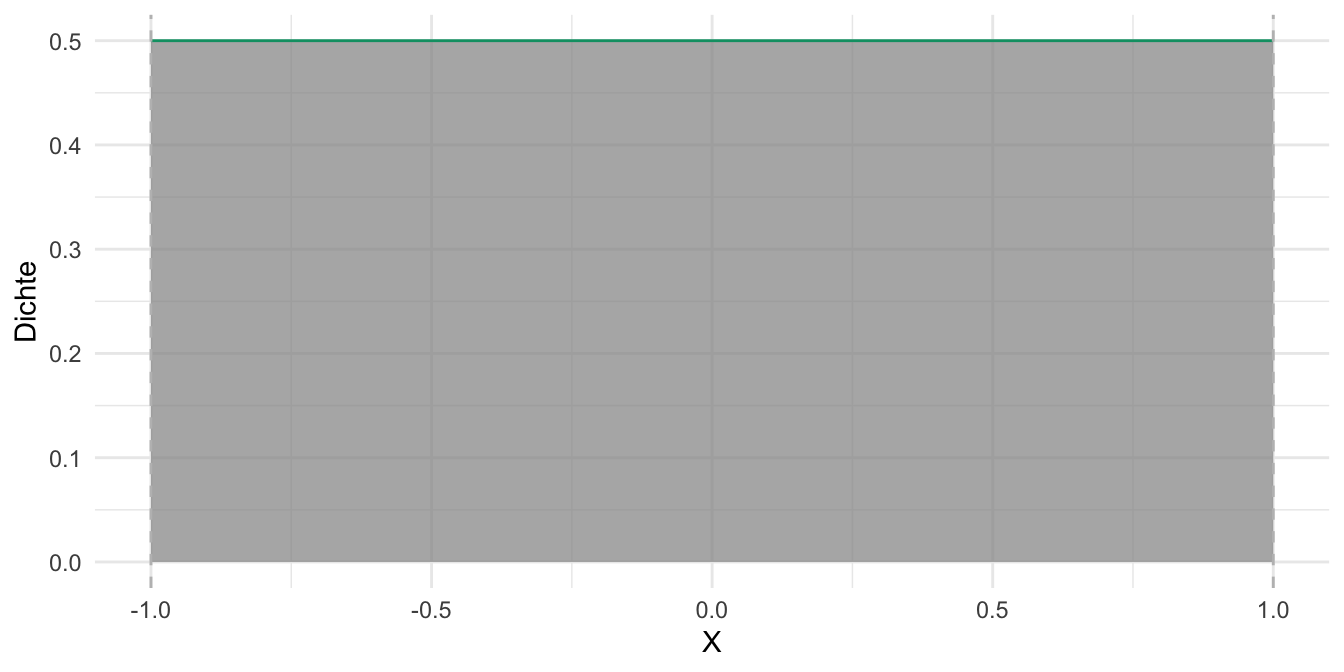
Eine Gleichverteilung nimmt an, dass jede Ausprägung der zugehörigen Zufallsvariablen gleichwahrscheinlich ist. Wenn man keinen hinreichenden Grund hat, eine bestimmte Ausprägung einer Zufallsvariablen für plausibler als einen anderen zu halten, ist eine Gleichverteilung eine passende Verteilung. Gleichverteilungen gibt es im diskreten und im stetigen Fall.

Abb. Abbildung 5.1 zeigt ein Beispiel für eine (stetige) Gleichverteilung.

(a) Beispiel a: Gleichverteilung min=-1, max=1. Dichte: 1/2

(b) Beispiel b: Gleichverteilung min=0, max=3. Dichte: 1/3

Abbildung 5.1: Stetige Gleichverteilung; man beachte jeweils die Y-Achse

Abbildung 5.1, (a): Bei $X=0$ hat eine Einheit von $X$ (z.B. von -1 bis 0) die Wahrscheinlichkeitsmasse von 50%, da der Bereich $[-1,0]$ die Hälfte (50%) der Wahrscheinlichkeitsmasse der Verteilung beinhaltet. Bei jedem anderen Punkt $x$ ist die Dichte identisch. Abbildung 5.1, (b): Bei $X=0$ hat eine Einheit von $X$ die Wahrscheinlichkeitsmasse von ca. 33%, da der Bereich $[0,1]$ ein Drittel der Wahrscheinlichkeitsmasse der Verteilung beinhaltet. Bei jedem anderen Punkt $x$ ist die Dichte identisch Definierendes Kennzeichen einer Gleichverteilung ist die konstante Dichte.

5.4 Binomialverteilung

5.4.1 Grundlagen

Definition 5.2 (Binomialverteilung) Die Binomialverteilung dient zur Darstellung der Wahrscheinlichkeit der Ergebnisse eines $n$-fach wiederholten binomialen Zufallexperiments, eines Zufallsexperiments mit zwei¹ Ergebnissen bzw. Elementarereignissen also. Dabei interessiert uns nur die Anzahl der $k$ Treffer, aber nicht die Reihenfolge. Bei jeder Wiederholung liegt die Wahrscheinlichkeit eines Treffers bei $p$. bleibt die Wahrscheinlichkeit der Ergebnisse gleich: Die Münze verändert sich nicht durch die Würfe (Ziehen mit Zurücklegen, ZmZ). Außerdem hat ein bestimmtes Ergebnis im ersten Wurf keinen Einfluss auf die Wahrscheinlichkeit eines bestimmten Ergebnisses im zweiten Wurf, etc., sog. “iid”: independent and identically distributed.] $◻$

$$\begin{array}{}\text{(5.1)}& \stackrel{\text{Unsere Zufallsvariable}}{\overbrace{X}}\underset{\text{ist verteilt nach der}}{\underbrace{\sim }}\underset{\text{mit den Parametern n, p}}{\underbrace{\stackrel{\text{Binomialverteilung}}{\overbrace{\text{Bin}(n,p)}}}}\end{array}$$

Für eine binomialverteilte Zufallsvariable $X$ schreibt man kurz wie in Theorem 5.1 gezeigt.

Theorem 5.1 (Notation für eine binomialverteilte Zufallsvariable) $$X\sim \text{Bin}(n,k)◻$$

Beispiel 5.1 Anwendungsbeispiele: Wie viele defekte Teile sind in einer Stichprobe von produzierten Schrauben zu erwarten? Wie wahrscheinlich ist es, dass das neue Blutdruck-Medikament einer bestimmten Anzahl von Menschen hilft? Wie viele Personen stimmen in einer Umfrage der Frage “Ich halte die öffentlich-rechtlichen Sender für wichtig.” zu? Was ist die Wahrscheinlichkeit, 6 mal hintereinander eine 6 zu würfeln bei einem fairen Würfel? Eine Münze, die in 7 von 10 Würfen “Kopf” zeigt – sollte sie als “unfair” eingeschätzt werden? $◻$

Stellen wir uns eine Kistchen² mit sehr vielen³ Losen vor, darunter 2/5 Treffer (Gewinn) und 3/5 Nieten, s. Abb. Abbildung 5.2. Der Versuch läuft so ab: Wir ziehen ein Los, schauen ob es ein Treffer ist oder nicht, legen es zurück und ziehen erneut. Da sehr viele Lose im Kästchen liegen, ist es praktisch egal, ob wir das Los wieder zurücklegen. Die Wahrscheinlichkeit für einen Treffer ändert sich (so gut wie) nicht. Jetzt ziehen wir z.B. drei Lose. Wie groß ist die Wahrscheinlichkeit, davon 2 Treffer zu erzielen (egal in welcher Reihenfolge)?

Abbildung 5.2: Ein Loskästchen mit 2/5 Treffer und 3/5 Nieten

Praktischerweise ist die Binomialverteilung in R eingebaut,
hier ist Pseudocode für Ihre Anwendung, s. Listing 5.1.

Listing 5.1: R-Pseudocode für die Binomialverteilung

dbinom(x = <Anzahl der Treffer>, 
       size = <Anzahl der Würfe>, 
       prob = <Wahrscheinlichkeit eines Treffers>)

5.4.2 Möglichkeiten zählen

Beispiel 5.2 (Drei Lose gekauft, davon zwei Treffer?) Wie groß ist die Wahrscheinlichkeit $p$ bei $n=3$ Zügen $k=2$ Treffer zu erzielen (und $n-k=1$ Niete)? (Nennen wir dieses gesuchte Ereignis der Kürze halber $A^{\prime }$). Die Trefferwahrscheinlichkeit ist (bei jedem Zug) $p=2/5$ und die Nietenwahrscheinlichkeit $1-p=3/5◻$, s. Abbildung 5.3. Abbildung 4.7 zeigt den entsprechenden Baum; Tabelle 5.1 zeigt die Ergebnisse dieses Zufallsexperiments.

Abbildung 5.3: Wie viele Möglichkeiten gibt es, 3 Lose zu sortieren, von denen 2 Treffer sind und 1 Niete?

Tabelle 5.1: Alle acht Ergebnisse des Zufallsexperiment (binär, 3-fach wiederholt) mit ihren Wahrscheinlichkeiten im Überblick

Pfad (Ereignis)	Anzahl Treffer	Wahrscheinlichkeit
TTT	3	$p^3={\left(\frac{2}{5}\right)}^3=\frac{8}{125}\approx 0.064$
TTN	2	$p^{2}q=\frac{4}{25}\cdot \frac{3}{5}=\frac{12}{125}\approx 0.096$
TNT	2	$p^{2}q=\frac{12}{125}\approx 0.096$
NTT	2	$p^{2}q=\frac{12}{125}\approx 0.096$
TNN	1	$p{q}^2=\frac{2}{5}\cdot \frac{9}{25}=\frac{18}{125}\approx 0.144$
NTN	1	$p{q}^2=\frac{18}{125}\approx 0.144$
NNT	1	$p{q}^2=\frac{18}{125}\approx 0.144$
NNN	0	$q^3={\left(\frac{3}{5}\right)}^3=\frac{27}{125}\approx 0.216$

Mit Blick auf Beispiel 5.2: Wir könnten jetzt ein Baumdiagramm zeichnen und pro Pfad die Wahrscheinlichkeit ausrechnen (Multiplikationssatz, Theorem 4.9), vgl. Abbildung 4.7. Die Summe der Wahrscheinlichkeiten der Pfade ist dann die gesuchte Wahrscheinlichkeit (Additionssatz, Theorem 4.1). Diagramme zeichnen ist einfach, dauert aber.

Beachtet man die verschiedenen Reihenfolgen nicht, so zählt man 3 günstige Pfade (T: Treffer; N: Niete), s. Abbildung 4.7:

1. TTN
2. TNT
3. NTT.

Wir haben also die Möglichkeiten (2 Treffer und 1 Niete zu erhalten)

• ohne Beachtung der Reihenfolge und
• ohne Zurücklegen (der Möglichkeiten)

gezählt.

Schneller geht es, wenn man rechnet. Wir könnten auch R auffordern, die Anzahl der günstigen Pfade zu berechnen, s. Theorem 5.3 mit choose(3,2), was die Antwort 3 liefert.

5.4.3 Anzahl Pfade mal Pfad-Wahrscheinlichkeit

In diesem Fall ist die Wahrscheinlichkeit eines (günstigen) Pfades, $A$:

$Pr(A)=Pr(T{)}^2\cdot Pr(N{)}^1={\left(\frac{2}{5}\right)}^2\cdot {\left(\frac{3}{5}\right)}^1\approx 0.096$.

p_a = (2/5)^2 * (3/5)^1
p_a
## [1] 0.096

Damit ist die Wahrscheinlichkeit des gesuchten Ereignisses $A^{\prime }$ (2 Treffer bei 3 Zügen) gleich der Anzahl der günstigen $k$ Pfade (3) mal der Wahrscheinlichkeit eines Pfades (0.1):

$Pr(A^{\prime })=k\cdot Pr(A)=3\cdot 0.096=0.29$.

p_a_strich = 3 * p_a
p_a_strich
## [1] 0.29

Die Wahrscheinlichkeit, bei 3 Zügen 2 Treffer zu erzielen, beträgt also ca. 29%.

Dabei steht $k$ für die Anzahl der günstigen Pfade und $Pr(A)$ für die Wahrscheinlichkeit eines günstigen Pfades (d.h. 2 Treffer und 1 Nieten) und alle Pfade haben die gleiche Wahrscheinlichkeit.

5.4.4 Formel der Binomialverteilung

Theorem 5.2 zeigt die mathematische Definition der Binomialverteilung. Dabei liegt immer ein Zufallsversuch mit $n$ Durchgängen und $k$ Treffern zugrunde. Jeder Durchgang hat die Trefferwahrscheinlichkeit $p$ und jeder Durchgang ist unabhängig von allen anderen.

Theorem 5.2 (Binomialverteilung) $$Pr(X=k|p,n)=\frac{n!}{k!(n-k)!}{p}^k(1-p{)}^{n-k}◻$$

Theorem 5.2 kann wie folgt auf Deutsch übersetzen:

Die Wahrscheinlichkeit für das Ereignis $X$ gegeben $p$ und $n$ berechnet als Produkt von zwei Termen. Der erste Term ist der Quotient von der Fakultät von n im Zähler und im Nenner das Produkt von erstens der Fakultät von k mit zweitens der Fakultät von (n-k). Der zweite Term ist das Produkt von p hoch k mal der komplementären Wahrscheinlichkeit von p hoch (n-k).

Oder noch kürzer:

Die Wahrscheinlichkeit für das Ereignis “X” gegeben p und k berechnet als Produkt von zwei Termen. Erstens der Anzahl der günstigen Pfade, k und zweitens der Wahrscheinlichkeit für einen günstigen Pfad, P(A).

Die Anzahl der (günstigen) Pfade kann man mit dem Binomialkoeffizient ausrechnen, den man so darstellt, s. Theorem 5.3.⁴

Definition 5.3 (Binomialkoeffizient) Der Binomialkoeffizient gibt an, auf wie vielen verschiedenen Arten man aus einer Menge von $n$ verschiedenen Objekten $k$ Objekte ziehen kann (ohne Zurücklegen und ohne Beachtung der Reihenfolge). $◻$

Theorem 5.3 (Binomialkoeffizient) $$(\genfrac{}{}{0ex}{}{n}{k})=\frac{n!}{k!(n-k)!}◻$$

Lies: “Wähle aus $n$ möglichen Ereignissen (Pfade im Baum) $k$ günstige Ereignisse (günstige Pfade) oder kürzer”k aus n”.

Um den Binomialkoeffizient zu berechnen, muss man die Fakultät berechnen. Die Fakultät ist eine Rechenvorschrift für natürliche Zahlen. Man schreibt sie mit einem Ausrufezeichen hinter der Zahl, also zum Beispiel $3!$. Dabei multipliziert man alle natürlichen Zahlen von der gegebenen Zahl bis hinunter zur 1.

Beispiel 5.3  

• $3!=3\cdot 2\cdot 1$
• $4!=4\cdot 3\cdot 2\cdot 1$
• $0!=1$ (per Definition) $◻$

Puh, Formeln sind vielleicht doch ganz praktisch, wenn man sich diese lange Übersetzung der Formel in Prosa duchliest. Noch praktischer ist es aber, dass es Rechenmaschinen gibt, die die Formel kennen und für uns ausrechnen.

Beispiel 5.4 (Klausur mit 20-Richtig-Falsch-Fragen) Ei Professi stellt einen Klausur mit 20 Richtig-Falsch-Fragen. Wie groß ist die Wahrscheinlichkeit, durch bloßes Münze werfen genau 15 Fragen richtig zu raten?⁵

# Wskt für genau 15 Treffer bei 20 Versuchen mit einer fairen Münze:
dbinom(x = 15, size = 20, prob = .5)
## [1] 0.015

Die Wahrscheinlichkeit liegt bei ca 1%.

Um höchstens 15 Treffer zu erzielen, müssten wir die Wahrscheinlichkeiten von 0 bis 15 Treffern aufsummieren.

Praktischerweise gibt es einen R-Befehl, der das Aufsummieren für uns übernimmt: pbinom.

pbinom(q = 15, size = 20, prob = .5)
## [1] 0.99

Die Wahrscheinlichkeit höchstens 15 Treffer (d.h. 0, 1, 2, … 15 Treffer) zu erzielen, liegt für prob = .5 laut Binomialverteilung mit pbinom bei gut 99%.

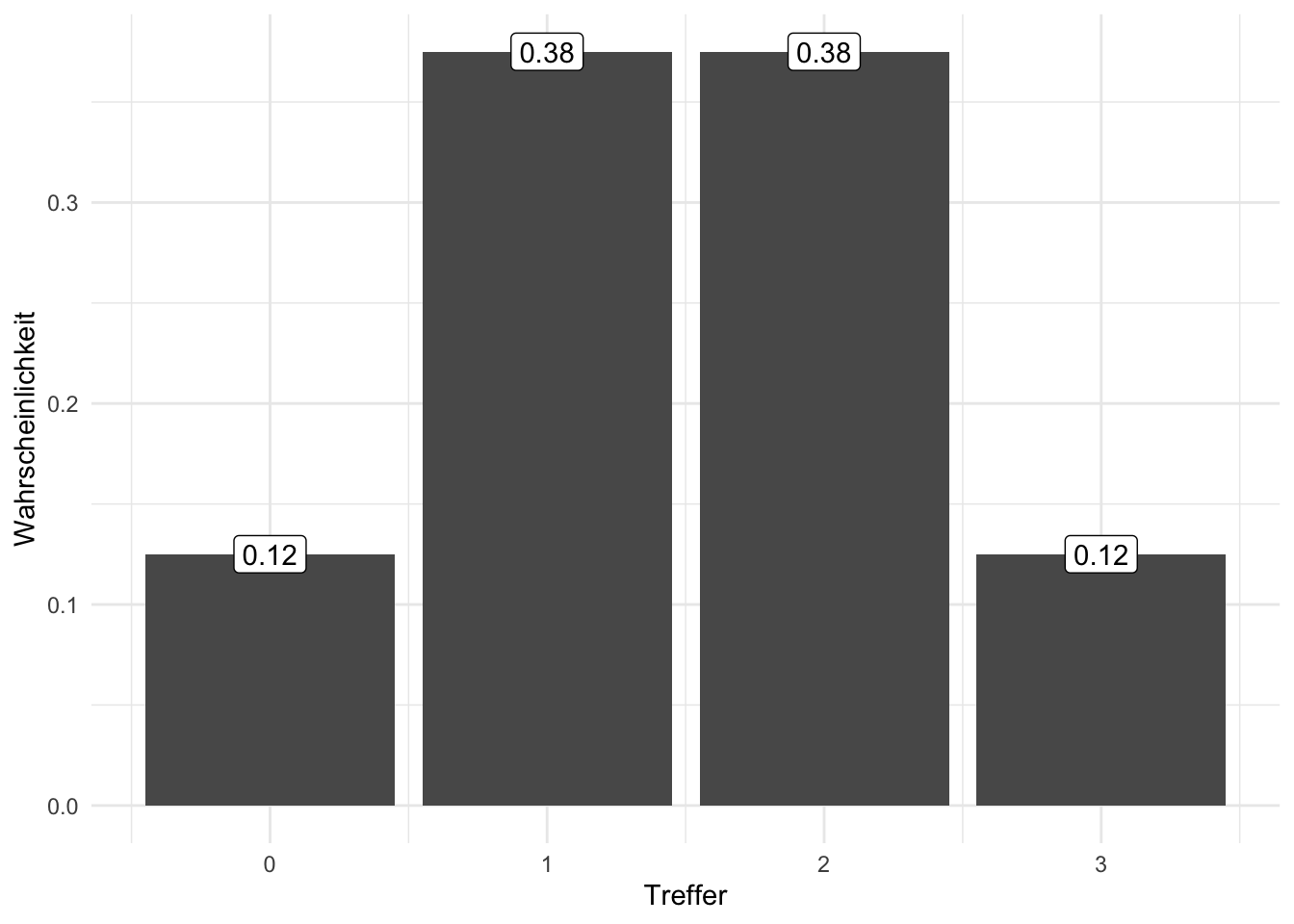
Beispiel 5.5 (3 Münzwürfe mit 3 Treffern) Was ist die Wahrscheinlichkeit bei 3 Münzwürfen (genau) 3 Treffer (Kopf) zu erzielen, s. Abbildung 5.4, links?

Das ist eine Frage an die Binomialverteilung; in R kann man das mit der Funktion dbinom beantworten.

dbinom(x = 3, size = 3, prob = 1/2)
## [1] 0.12

Die Lösung lautet also $p=1/8=.125.◻$

Man kann sich auch vor Augen führen, dass es genau 1 günstigen Pfad gibt, nämlich TTT. Nach dem Multiplikationssatz gilt also: $Pr(X=3)=1\cdot {\left(\frac{1}{2}\right)}^3=\frac{1}{8}=.125$.

loesung <- (1/2)^3
loesung
## [1] 0.125

(a) n=3, p=1/2

(b) n=9, p=.7

Abbildung 5.4: Verschiedene Binomialverteilungen

Übungsaufgabe 5.1 ️ Was fällt Ihnen bei der Binomialverteilung auf? Ist sie symmetrisch? Verändert sich die Wahrscheinlichkeit von einer Trefferzahl zur nächsten linear?

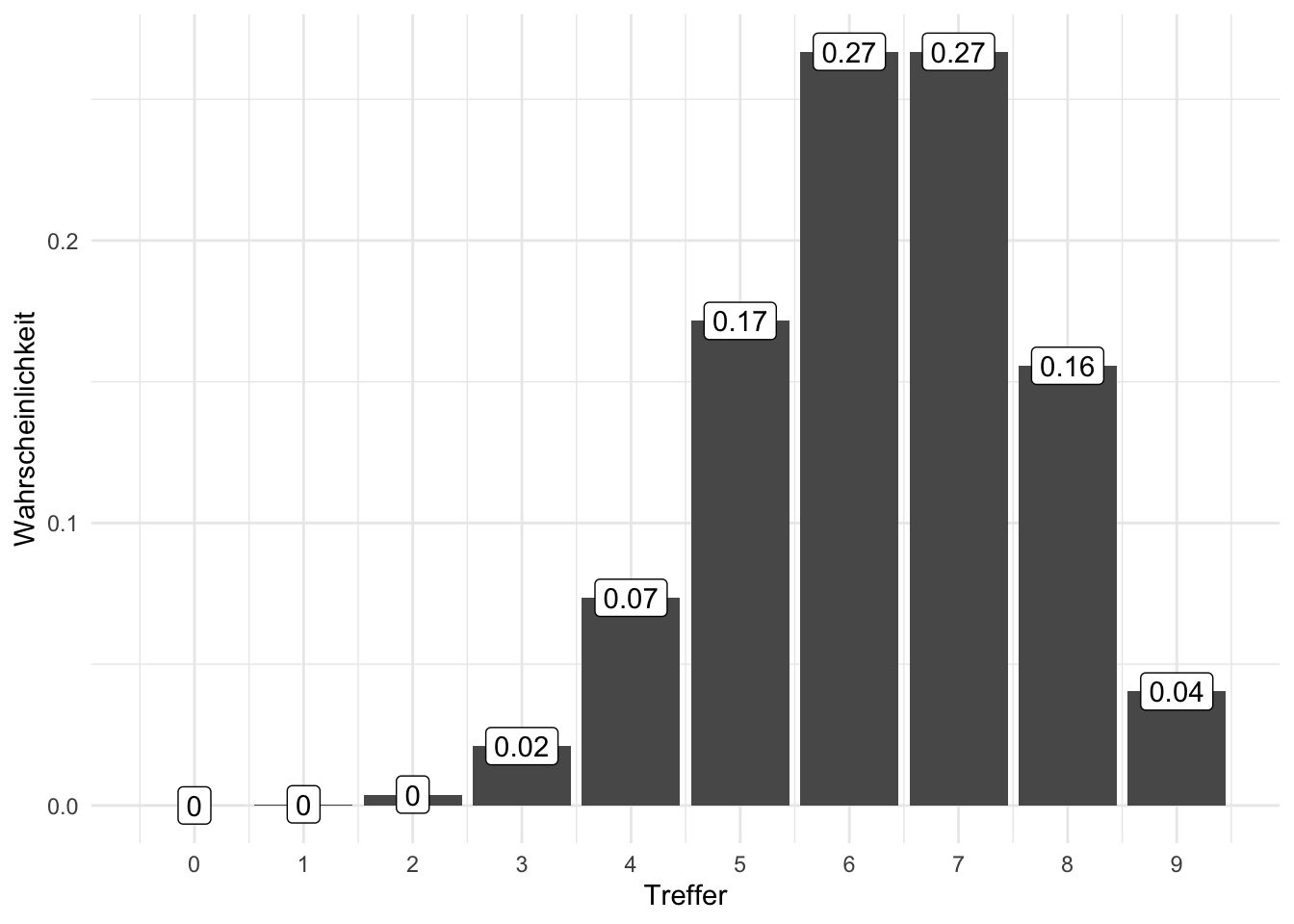
Übungsaufgabe 5.2 Was ist die Wahrscheinlichkeit für 0, 1, 2, …, 9 Treffern bei 9 Würfen, wenn die Trefferwahrscheinlichkeit 70% beträgt? Abbildung 5.4, rechts, zeigt die Antwort.

5.4.5 Rechnen mit der Binomialverteilung

Die Binomialverteilung ist in R eingebaut; man kann sich leicht entsprechende Wahrscheinlichkeiten ausrechnen lassen: z.B. dbinom(x = 2, size = 3, prob = 2/5). Das ist komfortabler als selber rechnen. Mit diesem Befehl rechnet R aus, wie hoch die Wahrscheinlichkeit ist, bei size = 3 “Münzwürfen”, x = 2 Treffer zu erzielen, wobei die Trefferwahrscheinlichkeit jeweils prob = 2/5 beträgt.

Beispiel 5.6 (Lotto) Wie viele Zahlenkombinationen gibt es im Lotto für 6 Richtige? Der Binomialkoeffizient verrät es uns: $(\genfrac{}{}{0ex}{}{49}{6})=13983816◻$ Ander gesagt: Der Binomialkoeffizient sagt uns, wie viele Möglichkeiten es gibt, aus z.B. 46 Bällen 6 zu ziehen (ohne Beachtung der Reihenfolge und ohne Zurücklegen). $◻$

Beispiel 5.7 Wie viele Möglichkeiten gibt es, 2 Treffer bei 4 Zügen zu erzielen?

Das sind folgende Ergebnisse: 1. TTNN, 2. TNTN, 3. TNNT, 4. NTTN, 5. NTNT, 6. NNTT.

$(\genfrac{}{}{0ex}{}{4}{2})=\frac{4!}{2!\cdot (4-2)!}\stackrel{\text{kürzen}}{=}\frac{2\cdot 3}{1}=6$

Es sind also 6 Möglichkeiten.

In R kann man sich die Fakultät mit dem Befehl factorial ausrechnen lassen. Der R-Befehl choose berechnet den Binomialkoeffizienten.⁶

anzahl_pfade_2_aus_4 <- 
  factorial(4) / (factorial(2) * factorial(4-2))
anzahl_pfade_2_aus_4
## [1] 6

choose(4, 2)
## [1] 6

$◻$

Beispiel 5.8 Hier sind die 10 Kombinationen, um aus 5 Losen genau 2 Treffer und 3 Nieten zu ziehen:

TTNNN, TNTNN, TNNTN, TNNNT, NTTNN, NTNTN, NTNNT, NNTTN, NNTNT, NNNTT

choose(5, 2)
## [1] 10

anzahl_pfade_2_aus_5 <- 
  factorial(5) / (factorial(2) * factorial(5-2))
anzahl_pfade_2_aus_5
## [1] 10

$◻$

Beispiel 5.9 (Beförderung) Aus einem Team mit 25 Personen sollen 11 Personen befördert werden. Wie viele mögliche Kombinationen (von beförderten Personen) können gebildet werden?

$(\genfrac{}{}{0ex}{}{25}{11})=\frac{25!}{11!\cdot (25-11)!}=4457400$

choose(n = 25, k = 11)
## [1] 4457400

Es gibt 4457400 Kombinationen von Teams; dabei ist die Reihenfolge der Ziehung nicht berücksichtigt.$◻$

5.4.6 Pumpstation-Beispiel zur Binomialverteilung

In einer Pumpstation arbeiten 7 Motoren, die wir als identisch annehmen. Mit einer Wahrscheinlichkeit von 5% fällt ein Motor aus und ist für den Rest des Tages nicht einsatzbereit. Der Betrieb kann aufrecht erhalten werden, solange mindestens 5 Motoren arbeiten. Wie groß ist die Wahrscheinlichkeit, dass die Pumpstation aus dem Betrieb fällt?

$Pr(X=k)$ (oder kurz: $Pr(k)$) gibt die Wahrscheinlichkeit (Wahrscheinlichkeitsfunktion) an für das Ereignis, dass k Motoren arbeiten.

Lassen wir R mal $Pr(X=5)$ ausrechnen.

dbinom(x = 5, size = 7, prob = .95)
## [1] 0.041

Es gilt also $Pr(X=5)\approx .04$. Die Wahrscheinlichkeit, dass (nur) 5 Motoren laufen an einem beliebigen Tag ist demnach relativ gering – wobei “gering” subjektiv ist, die Betreiberfirma findet diese Wahrscheinlichkeit, dass 2 Pumpen ausfallen, wohl viel zu hoch. Die Wahrscheinlichkeit, dass $k=0\dots 7$ Motoren laufen, ist in Abbildung 5.5 dargestellt.

dbinom() steht für die Wahrscheinlichkeitsdichte (im diskreten Fall, wie hier, Wahrscheinlichkeitsfunktion genannt) und binom für die Binomialverteilung. x gibt die Anzahl der Treffer an (das gesuchte Ereignis, hier 5 Motoren arbeiten); size gibt die Stichprobengröße an (hier 7 Motoren).

Damit gilt:

$Pr(X\ge 5)=Pr(X=5)+Pr(X=6)+Pr(X=7)$

Berechnen wir zunächst die Wahrscheinlichkeit, dass 5,6 oder 7 Motoren laufen mit Hilfe der Binomialverteilung.

p_5 <- dbinom(x = 5, size = 7, prob = .95)
p_6 <- dbinom(x = 6, size = 7, prob = .95)
p_7 <- dbinom(x = 7, size = 7, prob = .95)

p_5
## [1] 0.041
p_6
## [1] 0.26
p_7
## [1] 0.7

Das sind 0.04, 0.26, 0.7. Die gesuchte Wahrscheinlichkeit, p_mind_5, ist die Summe der drei Einzelwahrscheinlichkeiten.

p_mind_5 <- p_5 + p_6 + p_7

p_mind_5
## [1] 1

Die Wahrscheinlichkeit, dass mind. 5 Motoren arbeiten beträgt also ca. 1.

Das komplementäre Ereignis zu diesem Ereignis ist, dass nicht mind. 5 Motoren arbeiten, also höchstens 4 und es daher zu einem Ausfall kommt. Es gilt also $Pr(\overline{X})=1-Pr(X)$.

p_weniger_als_4 <- 1 - p_mind_5
p_weniger_als_4
## [1] 0.0038

Das sind also 0 also0.38 % Wahrscheinlichkeit, dass die Pumpstation ausfällt.

Abbildung 5.5: Wahrscheinlichkeit, dass genau k = 0..7 Motoren laufen

Alternativ kann man mit der Verteilungsfunktion pbinom() rechnen, die $Pr(X\le 4)$ berechnet.

In R kann man die Funktion pbinom() nutzen (p für (kumulierte) Wahrscheinlichkeit), um die Verteilungsfunktion der Binomialverteilung zu berechnen.

pbinom(q = 4, size = 7, prob = .95)
## [1] 0.0038

q = 4 steht für $X\le 4$, also für höchstens 4 Treffer (arbeitende Motoren); size = 7 meint die Stichprobengröße, hier 7 Motoren; prob gibt die Trefferwahrscheinlichkeit an. $◻$

Übungsaufgabe 5.3 (Peer-Instruction: Qualitätskontrolle in einer Fabrik) Eine Fabrik produziert USB-Sticks. Die Wahrscheinlichkeit, dass ein USB-Stick defekt ist, beträgt 2%. Aus der laufenden Produktion werden regelmäßig 10 USB-Sticks zufällig ausgewählt und getestet. Sei $X$ die Anzahl defekter USB-Sticks in dieser Stichprobe.

Welche Aussage ist richtig bzw. passt am besten?

1. Mit 98% sind alle 10 USB-Sticks in Ordnung.
2. Mit 82% sind alle 10 USB-Sticks in Ordnung.
3. Mit 2% sind alle 10 USB-Sticks defekt.
4. Es ist unmöglich, dass alle 10 USB-Sticks defekt sind.
5. Es ist unmöglihc, dass alle 10 USB-Sticks in Ordnung sind. $◻$

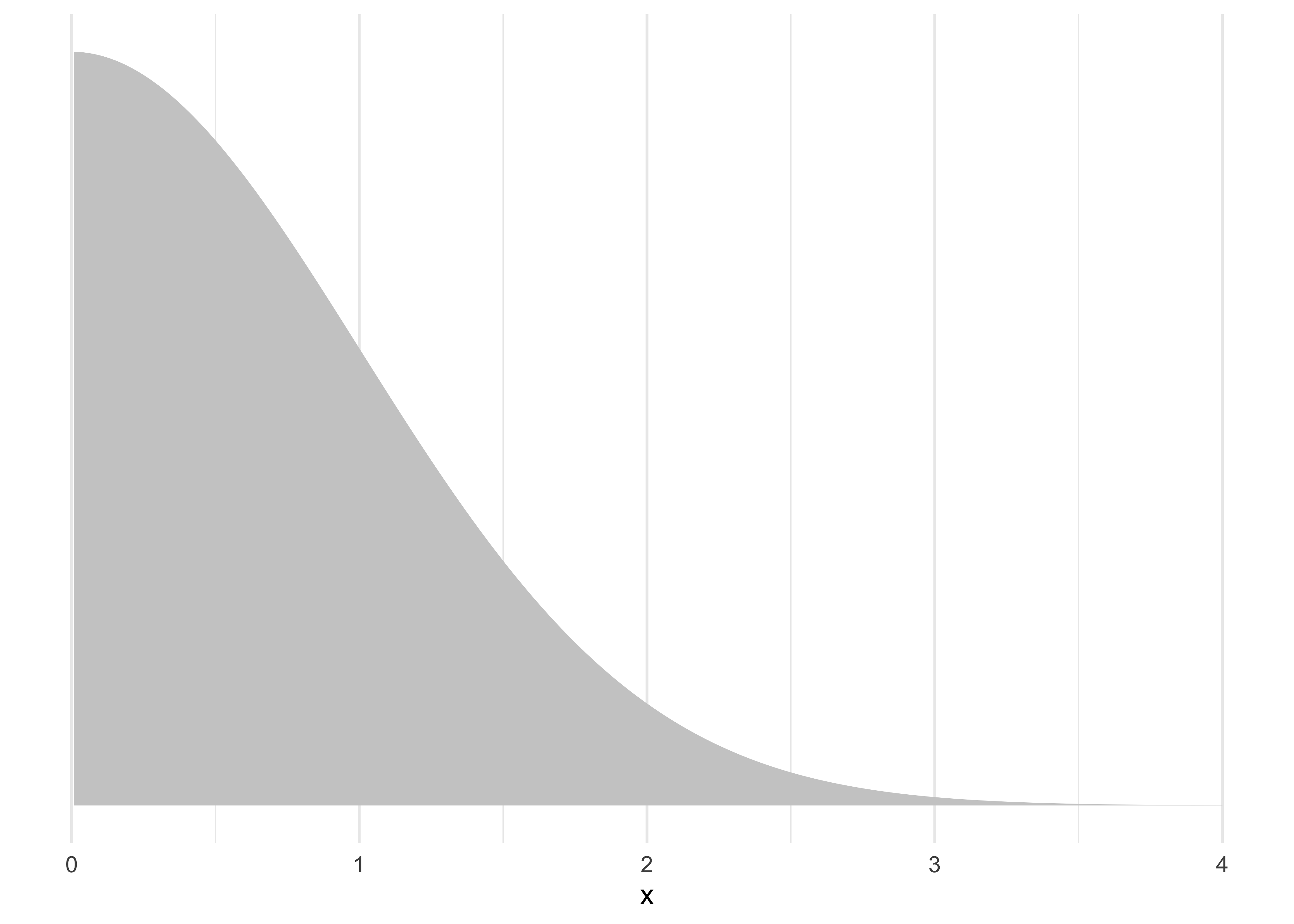
5.5 Die halbe Normalverteilung

Grundlagen über die Normalverteilung können in Sauer (2025) nachgelesen werden. Ein Spezialfall der Normalverteilung ist die halbe (oder halbseitige) Normalverteilung, s. Abbildung 5.6.

df <- data.frame(x = seq(-4, 4, length.out = 500))
df$y <- dnorm(df$x)

# Separate shading regions
df_left  <- subset(df, x <= 0) 
df_right <- subset(df, x >= 0)

ggplot(df, aes(x, y)) +
  geom_area(data = df_left, aes(x, y), fill = "grey90") +
  geom_area(data = df_right, aes(x, y), fill = "grey80") +
  #geom_line(size = 1) +
  theme_minimal() +
  scale_y_continuous(NULL, breaks = NULL) +
  theme(
    axis.title.y = element_blank(),
    axis.text.y  = element_blank(),
    axis.ticks.y = element_blank(),
    axis.line.y  = element_blank()
  ) +
  scale_x_continuous(limits = c(0, 4))

Abbildung 5.6: Die halbe Normalverteilung

Definition 5.4 (Halbe Normalverteilung) Wenn man die (negativen) Vorzeichen bei den Werten der Normalverteilung ignoriert, erhält man die halbe Normalverteilung. Man “spiegelt” die negative Seite auf die positive. $◻$

Man kann sie verwenden, wenn man von normalverteilten Werten ausgeht, die größer als Null sein müssen. Sie hat zwei Parameter, Mittelwert und SD, analog zur Normalverteilung.

Beispiel 5.10 (Halbe Normalverteilungen)  

• Die Entfernung Ihres Dart-Pfeiles zur Mitte der Zielscheibe
• Die Entfernung des vom Baum gefallenen Apfels zum Stamm
• Die Abweichung des Gewichts eines Produktionsgegenstands (z.B. einer Schraube) vom Soll-Gewicht
• Die Reaktionszeiten einer Versuchsperson in einer Reaktionszeitaufgabe $◻$

5.6 Die Exponentialverteilung

5.6.1 Die Apfel-fällt-nicht-weit-vom-Stamm-Verteilung

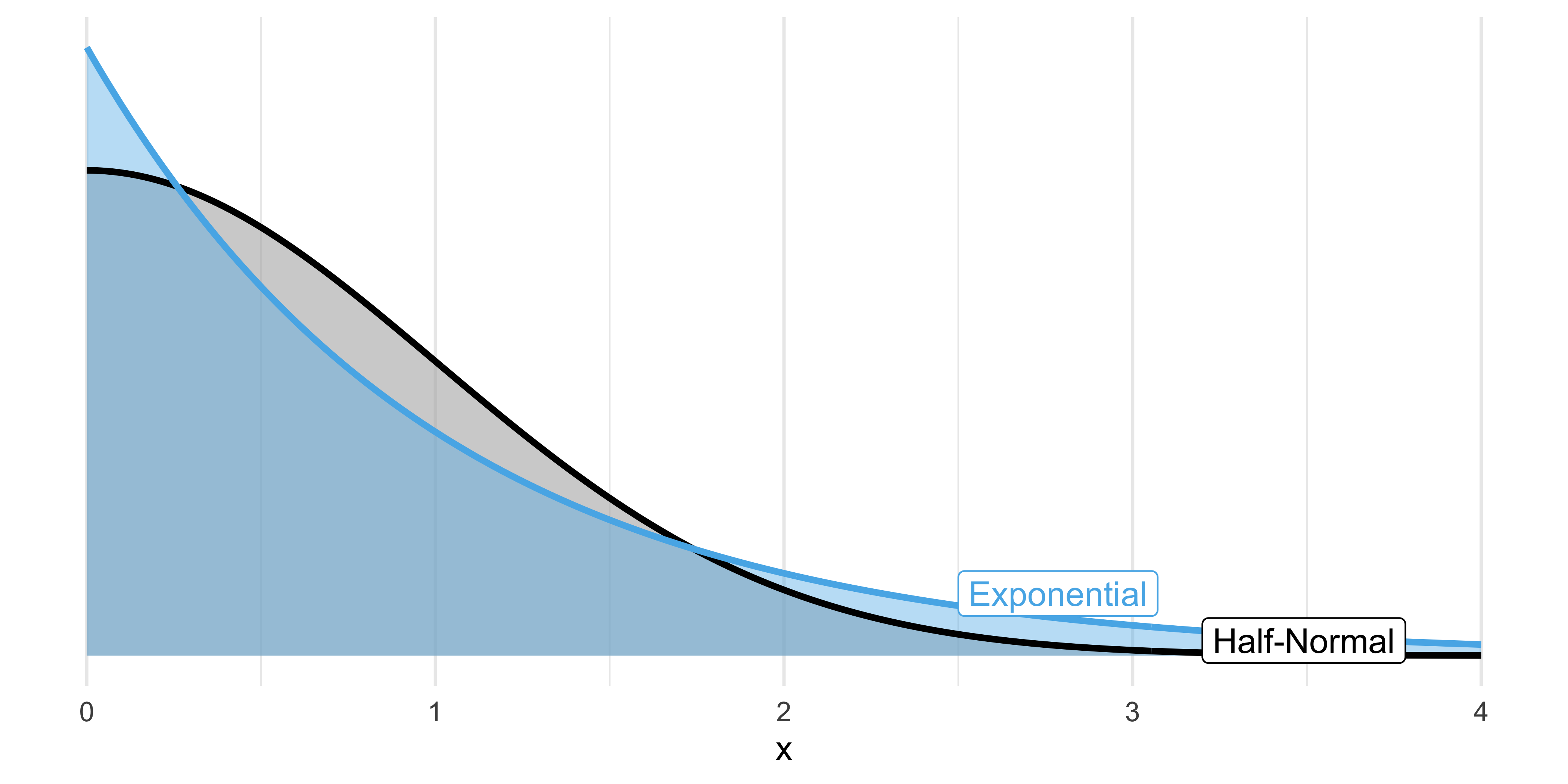
Anstelle der halben Normalverteilung man auch die Exponentialverteilung verwenden. Die beiden Verteilungen haben einen ähnlichen Verlauf, nur dass bei Exponentialverteilung Extremwerte wahrscheinlicher sind. Das kann vorteilhaft sein, wenn man ein Phänomen darstellen will, dessen Skalierung man nicht genau kennt. Die Normalverteilung setzt dem Streuung der Werte deutlich engere Grenzen als die Exponentialverteilung. Abbildung 5.7 stellt die beiden Verteilungen nebeneinander.

Abbildung 5.7: Exponentialverteilung (blau, Rate = 1) vs. halbe Normalverteilung (sd = 1)

Für eine exponentialverteilte Variable $X$ schreibt man auch:

$$X\sim \mathrm{Exp}(1)$$

Eine Verteilung dieser Form nennt man Exponentialverteilung. Sie hat einige nützliche Eigenschaften:

1. Eine Exponentialverteilung ist nur für positive Werte, $x>0$, definiert.
2. Steigt X um eine Einheit, so ändert sich Y um einen konstanten Faktor.
3. Sie hat nur einen Parameter, genannt Rate oder $\lambda$ (“lambda”).
4. $\frac{1}{\lambda }$ gibt gleichzeitig Mittelwert und Streuung (“Gestrecktheit”) der Verteilung an.
5. Je größer die Rate $\lambda$, desto schneller der “Verfall” der Kurve und desto kleiner die Streuung und der Mittelwert der Verteilung (und umgekehrt: Je größer $1/\lambda$, desto größer die Streuung und der Mittelwert der Verteilung.)

Ohne auf die mathematischen Eigenschaften im Detail einzugehen, halten wir fest, dass der Graph dieser Funktion gut zu unseren Plänen passt.

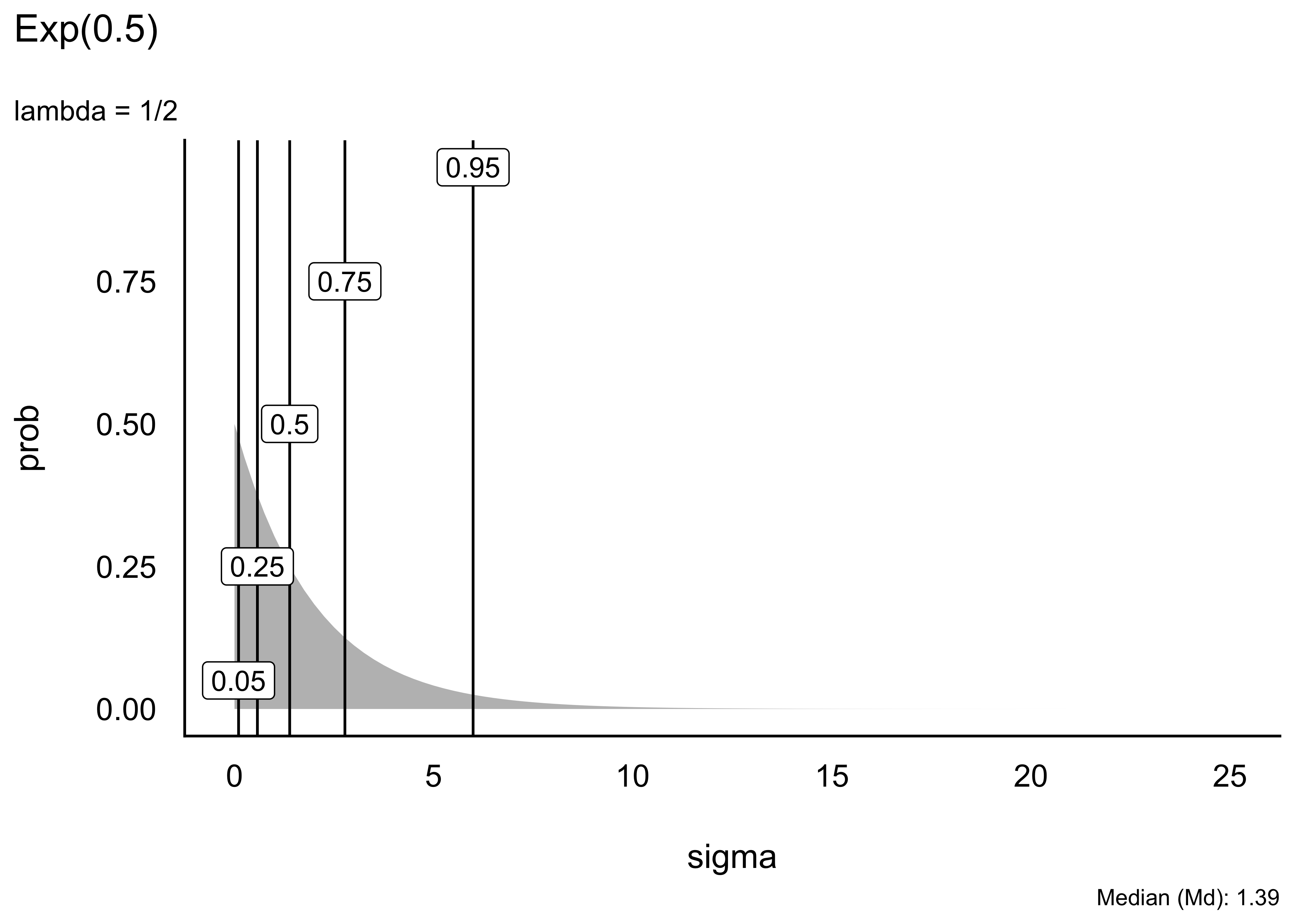
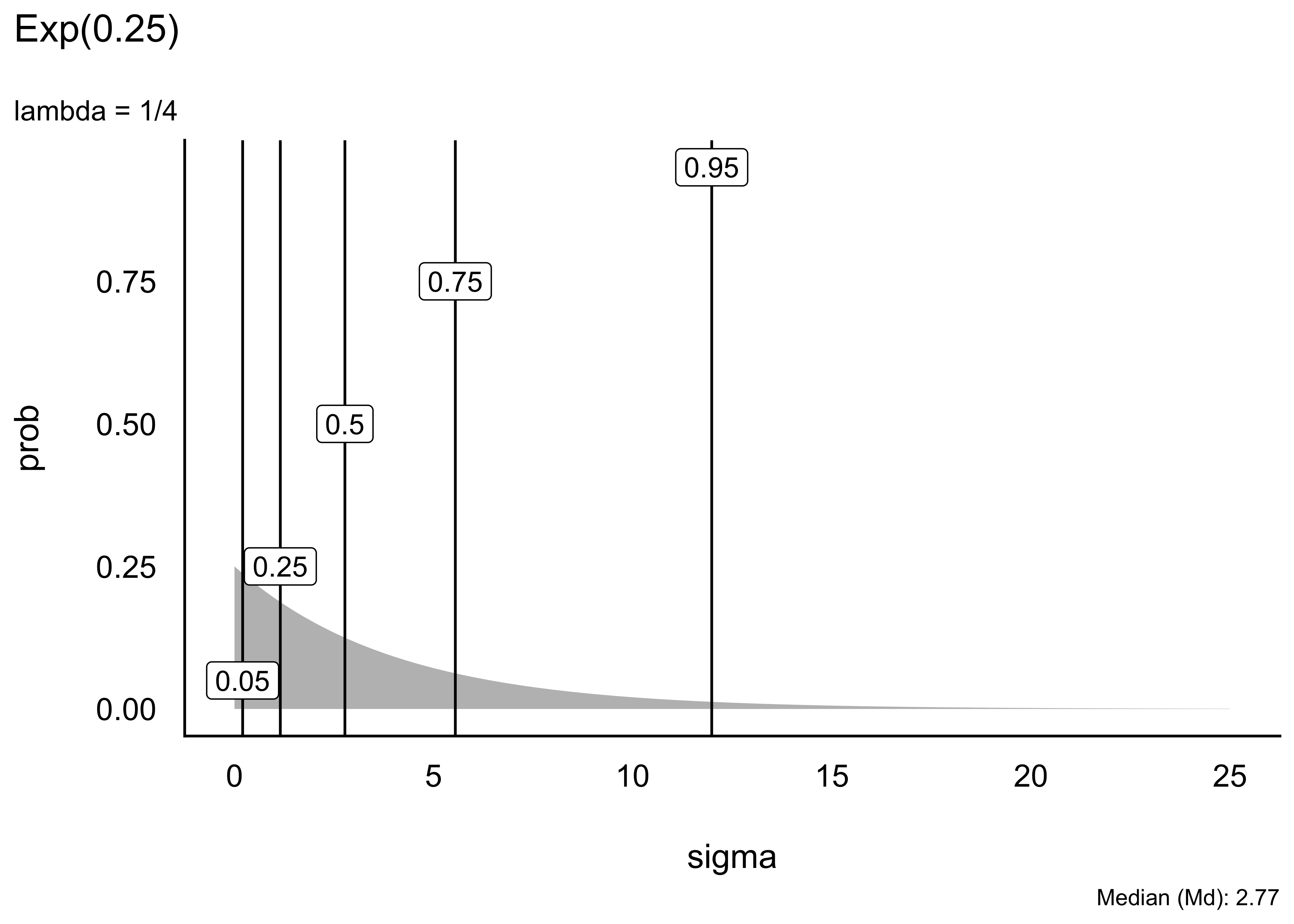
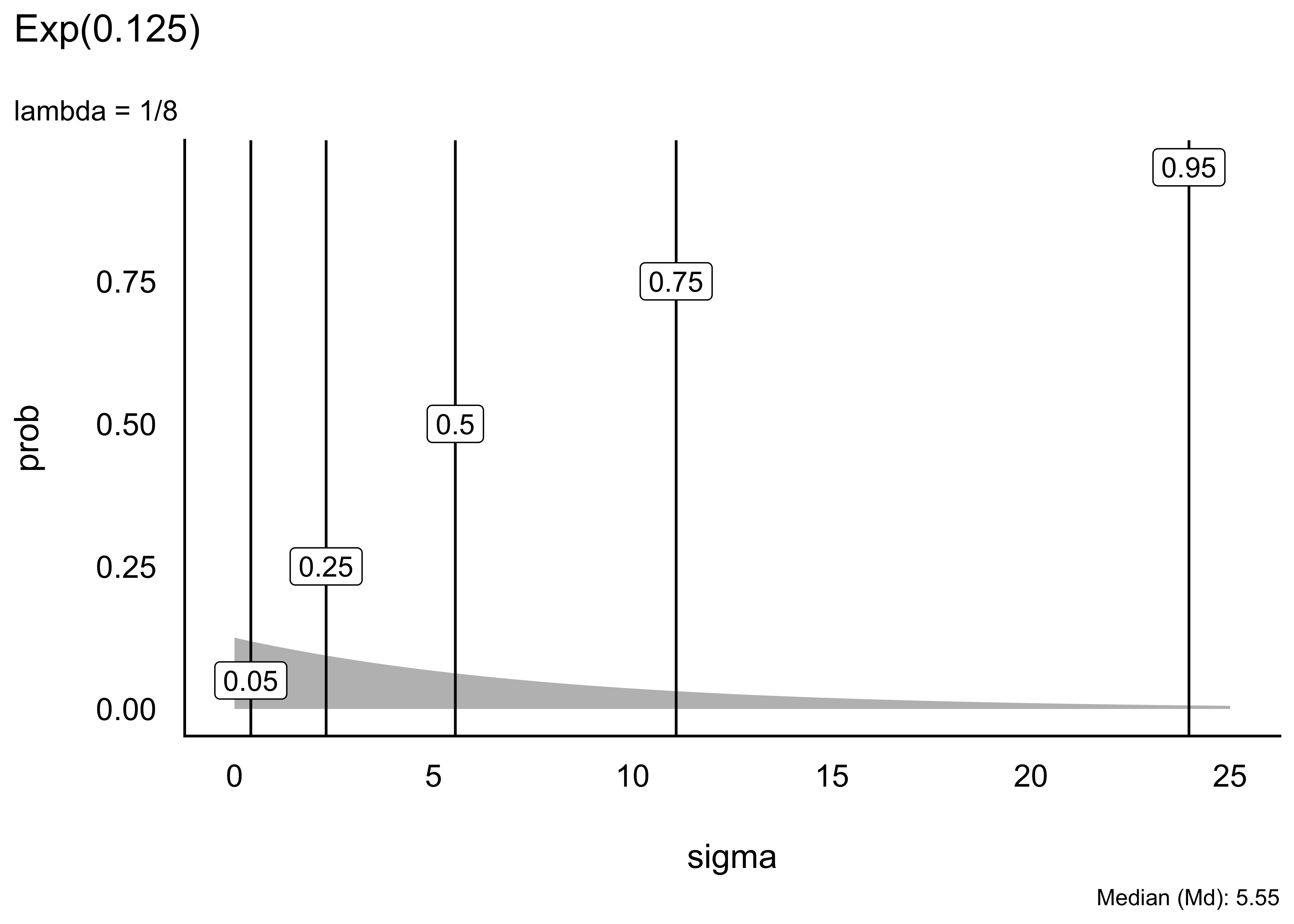
5.6.2 Visualisierung verschiedener Exponentialverteilungen

Schauen wir uns einige Beispiele von Exponentialverteilungen an. Unterschiede in Exponentialverteilungen sind rein auf Unterschiede in $\lambda$ (lambda) zurückzuführen, s. Abbildung 5.8.

lambda = 2

lambda = 1

lambda = 1/2

lambda = 1/4

lambda = 1/8

Abbildung 5.8

Hinweis

Eine “gut passende” oder gar die “richtige” Verteilung zu finden, ist nicht immer einfach, wenn nicht unmöglich. Gut beraten ist man mit der Regel, im Zweifel lieber eine liberale Verteilung zu wählen, die einen breiteren Raum an möglichen Werten zulässt. Allerdings sollte man nicht das Baby mit dem Wasser auskippen und extreme Werte, wie etwa mehrere Kilometer Körpergröße, besser verbieten.

Man kann sich den Median und andere Quantile der Exponentialverteilung mit qexp ausgeben lassen, wobei mit man p den Wert der Verteilungsfunktion angibt, für den man das Quantil haben möchte, z.B. p = .5 für den Mediaan (mit pexp() kann man sich analog die die Verteilungsfunktion ausgeben lassen.) Mit rate wird $\lambda$ (lambda) bezeichnet.⁷

Dieser Aufruf zum Beispiel, qexp(p = .5, rate = 1/8), gibt uns das 50%-Quantil einer Exponentialverteilung mit Rate ($\lambda$) 1/8 zurück, ca. 5.5: Mit einer Wahrscheinlichkeit von 50% wird ein Wert von 5.5 nicht überschritten bei dieser Verteilung.

Die Grenzen der inneren 95% dieser Verteilung kann man sich auch ausgeben.

qexp(p = c(0.025, .975), rate = 1/8)
## [1]  0.2 29.5

Tabelle Tabelle 5.2 zeigt die Mediane einiger Exponentialverteilungen, d.h. Exponentialverteilungen mit verschiedenen Werten für $\lambda$.

Tabelle 5.2: Median-Werte von Exponentialverteilungen mit verschiedenen Werten für λ (lambda).

lambda	p50	p95
100.00	0.01	0.03
50.00	0.01	0.06
8.00	0.09	0.37
4.00	0.17	0.75
2.00	0.35	1.50
1.00	0.69	3.00
0.50	1.39	5.99
0.25	2.77	11.98
0.12	5.55	23.97
0.02	34.66	149.79
0.01	69.31	299.57

5.7 Vertiefung

Bourier (2011), Kap. 6.2 und 7.1 erläutert einige (grundlegende) theoretische Hintergründe zu diskreten Zufallsvariablen und Wahrscheinlichkeitsverteilungen. Wichtigstes Exemplar für den Stoff dieses Kapitels ist dabei die Binomialverteilung.

Mittag & Schüller (2020) stellen in Kap. 12 und 13 Zufallsvariablen vor; zum Teil geht die Darstellung dort über die Lernziele bzw. Inhalte dieses Kurses hinaus.

5.8 Aufgaben

Zusätzlich zu den Aufgaben in der genannten Literatur sind folgende Aufgaben zu empfehlen.

5.8.1 Paper-Pencil-Aufgaben

• alphafehler-inflation3
• alphafehler-inflation4
• iq1a
• iq2a
• iq3a
• simu-uniform
• simu-unif2
• simu-unif3
• Quiz zum Thema Verteilungen
• Bsp-Binomial
• distros
• bfi10
• wskt-quiz10
• Schiefe1
• exp-tab
• exp1
• small-wide-normal
• likelihood-nv
• schmalstepost

5.8.2 Aufgaben, für die man einen Computer braucht

• alphafehler-inflation2
• Quiz (Aufgabensammlung) zu Verteilungen
• wuerfel01
• wuerfel02
• wuerfel03
• wuerfel04
• iq01
• iq02
• iq03
• iq04
• iq05
• iq06
• iq07
• iq08
• Bus1

5.9 —

Bourier, G. (2011). Wahrscheinlichkeitsrechnung und schließende Statistik: praxisorientierte Einführung mit Aufgaben und Lösungen (7., aktualisierte Aufl). Gabler.

Bourier, G. (2022). Statistik-Übungen: Beschreibende Statistik – Wahrscheinlichkeitsrechnung – Schließende Statistik (7. Auflage). Springer Gabler.

Mittag, H.-J., & Schüller, K. (2020). Statistik: Eine Einführung mit interaktiven Elementen. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-61912-4

Sauer, S. (2025). Statistik1. Independently published via Amazon. https://www.amazon.de/Statistik1-Einf%C3%BChrung-Statistik-Schwerpunkt-Prognose-Modellierung/dp/B0F673WGG5

---

1. von lat. bis “zweimal”

2. In den Lehrbüchern häufig als Urne bezeichnet, was den bösen Spott von “Friedhofstatistik” nach sich zog.

3. praktisch unendlich vielen

4. wobei gelten muss $n\ge k$

5. Hey, endlich mal was für echte Leben!

6. Bei Taschenrechnern ist diese Funktion oft als “nCr” zu finden.

7. Es gibt auch [Online-Apps, die diese Werte ausgeben](https://homepage.divms.uiowa.edu/~mbognar/applets/exp-like.html.