11  Konfundierung

11.1 Lernsteuerung

11.1.1 Position im Modulverlauf

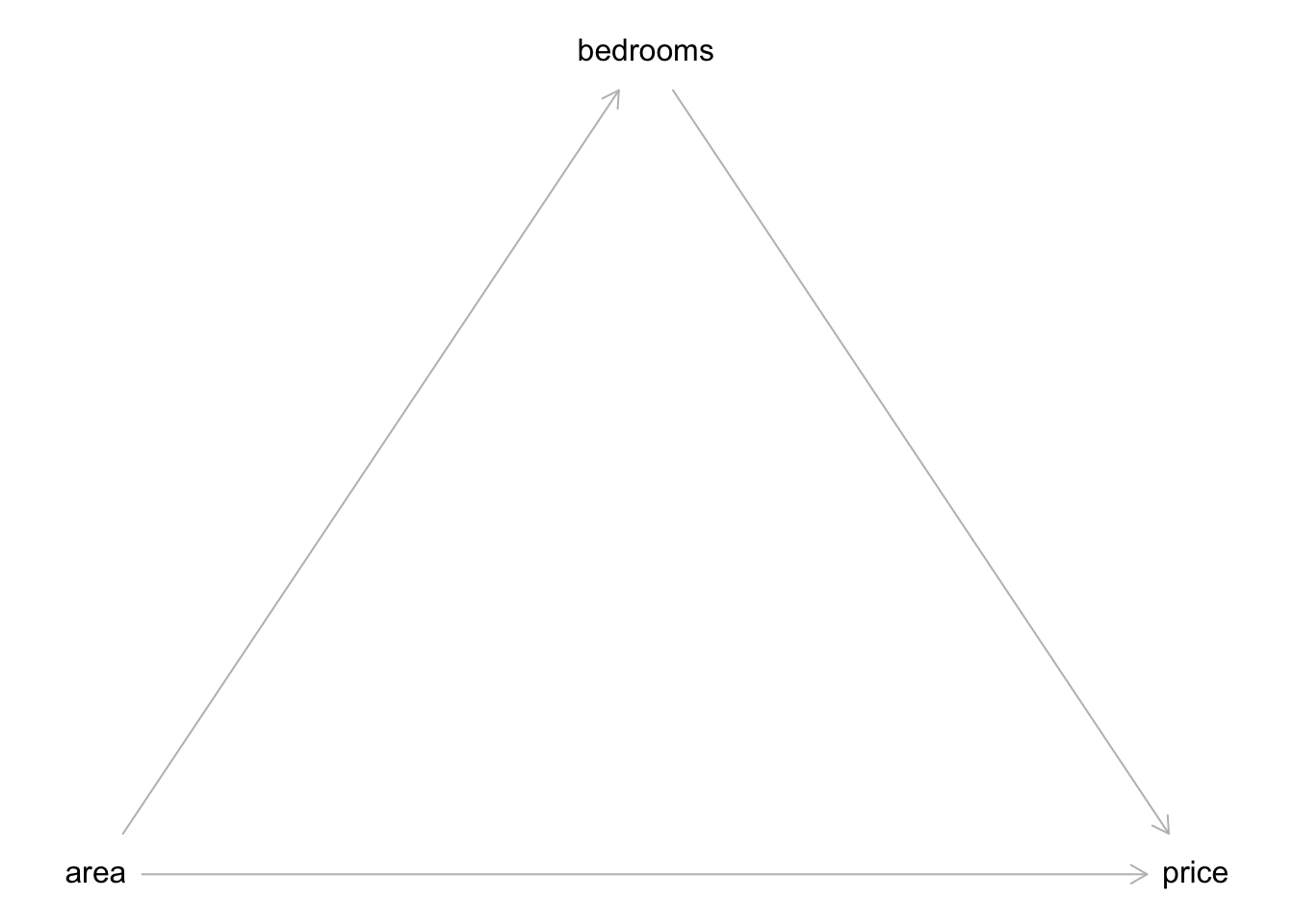
Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

11.1.2 R-Pakete

Für dieses Kapitel benötigen Sie folgende R-Pakete:

library(dagitty)  # DAGs zeichnen
library(tidyverse)
library(rstanarm)
library(easystats)

11.1.3 Daten

Wir nutzen den Datensatz Saratoga County; s. Tabelle 11.3. Hier gibt es eine Beschreibung des Datensatzes.

Sie können ihn entweder über die Webseite herunterladen:

SaratogaHouses_path <- "https://vincentarelbundock.github.io/Rdatasets/csv/mosaicData/SaratogaHouses.csv"

d <- read.csv(SaratogaHouses_path)

Oder aber über das Paket mosaic importieren:

data("SaratogaHouses", package = "mosaicData")
d <- SaratogaHouses  # kürzerer Name, das ist leichter zu tippen

11.1.4 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können …

• erklären, was eine Konfundierung ist
• DAGs lesen und zeichen
• Konfundierung in einem DAG erkennen

11.1.5 Begleitliteratur

Dieses Kapitel vermittelt die Grundlagen der Kausalinferenz mittels graphischer Modelle. Ähnliche Darstellungen wie in diesem Kapitel findet sich bei Rohrer (2018).

11.1.6 Überblick

In diesem Kapitel steigen wir ein in das Themengebiet Kausalanalyse (oder synonym Kausalinferenz). Wir beschäftigen uns also mit der für die Wissenschaft (und den Rest des Universums) zentralen Frage, was die Ursache eines Phänomens ist. In diesem ersten Kapitel zu dem Thema geht es um einen häufigen Fall von “Scheinkorrelation”, also eines Zusammenhangs zwischen UV und AV, der aber gar kein echter kausaler ist, sondern nur Schein. Bei diesem Scheinzusammenhang handelt es sich um die Konfundierung. Im nächsten Kapitel schauen wir uns die verbleibenden Grundbausteine der Kausalinferenz an.

11.1.7 Einstieg

11.1.8 Von Störchen und Babies

Kennen Sie die Geschichte von Störchen und Babies? Ich meine nicht die aus dem Biologieunterricht in der fünften Klasse, sondern in einem statistischen Zusammenhang. Was war da noch mal die Moral von der Geschichte?¹ \(\square\)

11.1.9 Erlaubt eine Regressionsanalyse Kausalschlüsse?

Findet man in einer Regressionsanalyse einen “Effekt”, also ein Regressionsgewicht ungleich Null, heißt das dann, dass die UV die Ursache der AV ist?² Erklären Sie diesen Sachverhalt genauer. \(\square\)

11.2 Statistik, was soll ich tun?

11.2.1 Studie A: Östrogen

11.2.1.1 Medikament einnehmen?

Mit Blick auf Tabelle 11.1: Was raten Sie dem Arzt? Medikament einnehmen, ja oder nein?

Tabelle 11.1: Daten zur Studie A

Gruppe	Mit Medikament	Ohne Medikament
Männer	81/87 überlebt (93%)	234/270 überlebt (87%)
Frauen	192/263 überlebt (73%)	55/80 überlebt (69%)
Gesamt	273/350 überlebt (78%)	289/350 überlebt (83%)

Die Daten stammen aus einer (fiktiven) klinischen Studie, \(n=700\), hoher Qualität (Beobachtungsstudie). Bei Männern scheint das Medikament zu helfen; bei Frauen auch. Aber insgesamt (Summe von Frauen und Männern) nicht?! Was sollen wir den Arzt raten? Soll er das Medikament verschreiben? Vielleicht nur dann, wenn er das Geschlecht kennt (Pearl et al., 2016)?

11.2.1.2 Kausalmodell zur Studie A

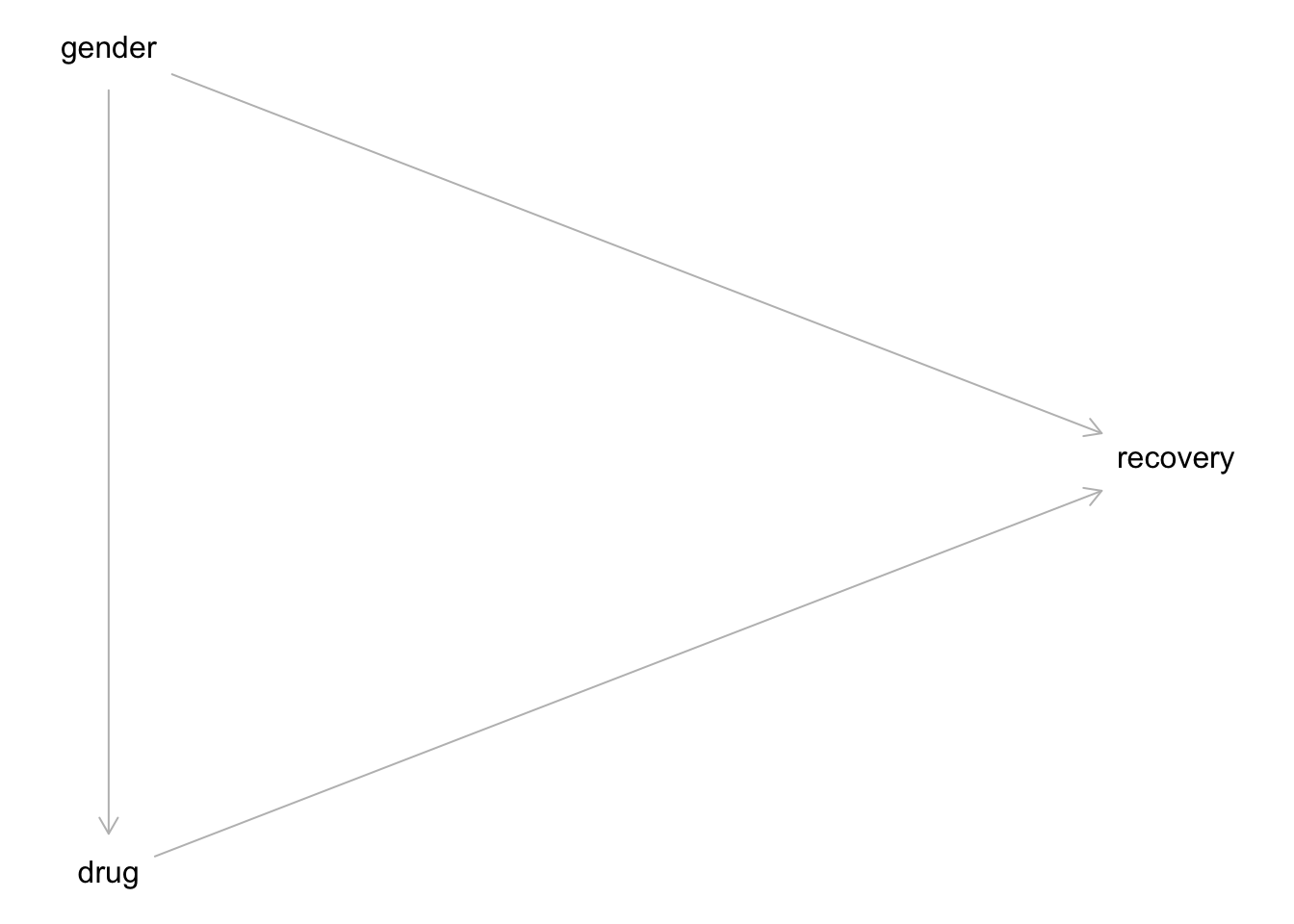
In Wahrheit sehe die kausale Struktur so aus: Das Geschlecht (Östrogen) hat einen Einfluss (+) auf Einnahme des Medikaments und auf Heilung (-). Das Medikament hat einen Einfluss (+) auf Heilung. Betrachtet man die Gesamt-Daten zur Heilung, so ist der Effekt von Geschlecht (Östrogen) und Medikament vermengt (konfundiert, confounded). Die kausale Struktur, also welche Variable beeinflusst bzw. nicht, ist in Abbildung 11.1 dargestellt.

Abbildung 11.1: Zwei direkte Effekte (gender, drug) und ein indirekter Effekt (gender über drug) auf recovery

Betrachtung der Gesamtdaten zeigt in diesem Fall einen konfundierten Effekt: Geschlecht konfundiert den Zusammenhang von Medikament und Heilung.

Wichtig

Betrachtung der Teildaten (d.h. stratifiziert pro Gruppe) zeigt in diesem Fall den wahren, kausalen Effekt. Stratifizieren ist also in diesem Fall der korrekte, richtige Weg. Achtung: Das Stratifizieren ist nicht immer und nicht automatisch die richtige Lösung. Stratifizieren bedeutet, den Gesamtdatensatz in Gruppen oder “Schichten” (“Strata”).

11.2.2 Studie B: Blutdruck

11.2.2.1 Medikament einnehmen?

Mit Blick auf Tabelle 11.2: Was raten Sie dem Arzt? Medikament einnehmen, ja oder nein?

Tabelle 11.2: Daten zur Wirksamkeit eines Medikaments (Studie B)

Gruppe	Ohne Medikament	Mit Medikament
geringer Blutdruck	81/87 überlebt (93%)	234/270 überlebt (87%)
hoher Blutdruck	192/263 überlebt (73%)	55/80 überlebt (69%)
Gesamt	273/350 überlebt (78%)	289/350 überlebt (83%)

Die Daten stammen aus einer (fiktiven) klinischen Studie, \(n=700\), hoher Qualität (Beobachtungsstudie). Bei geringem Blutdruck scheint das Medikament zu schaden. Bei hohem Blutdrck scheint das Medikamenet auch zu schaden. Aber insgesamt (Summe über beide Gruppe) nicht, da scheint es zu nutzen?! Was sollen wir den Arzt raten? Soll er das Medikament verschreiben? Vielleicht nur dann, wenn er den Blutdruck nicht kennt (Pearl et al., 2016)?

11.2.2.2 Kausalmodell zur Studie B

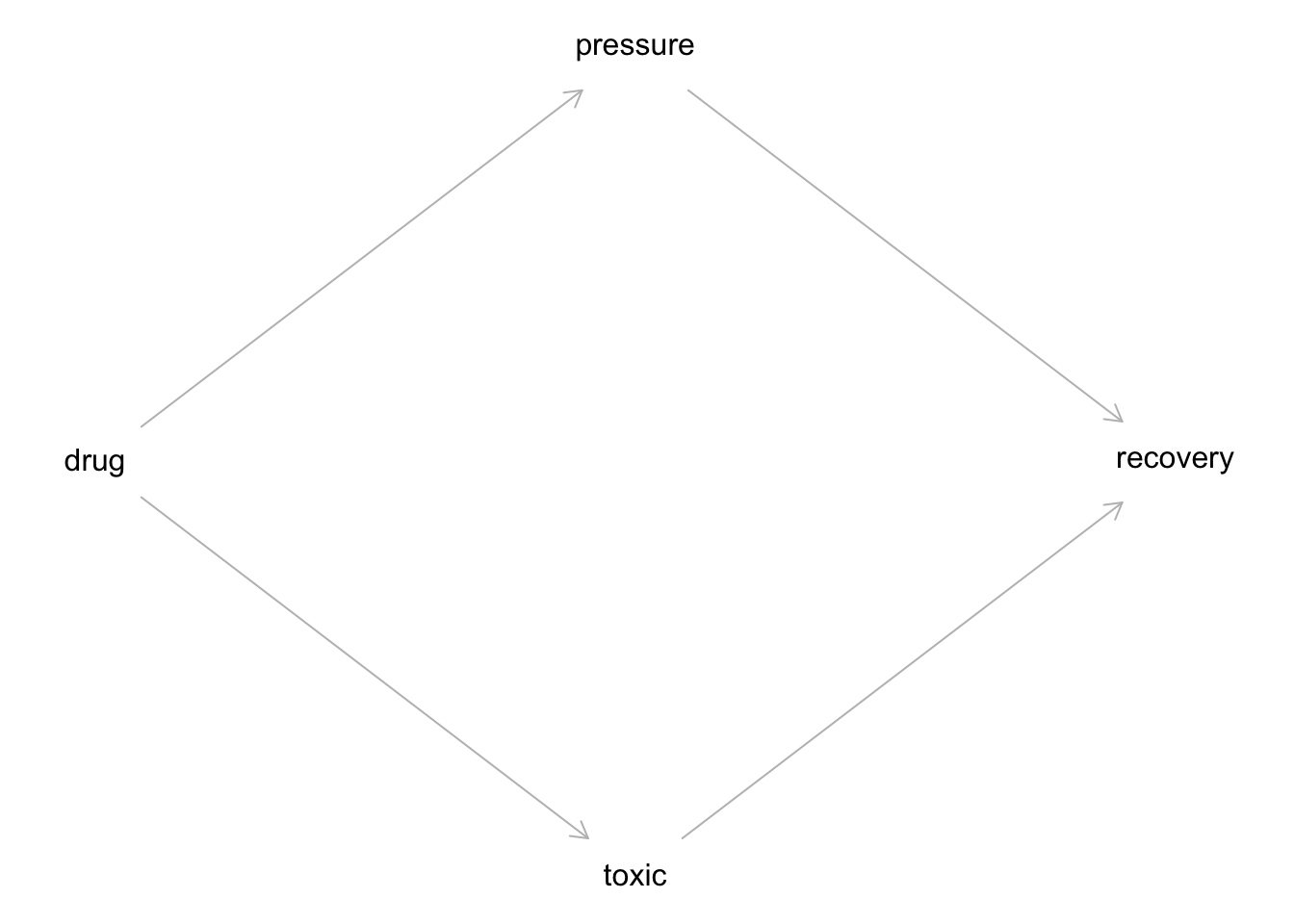
Das Medikament hat einen (absenkenden) Einfluss auf den Blutdruck. Gleichzeitig hat das Medikament einen (toxischen) Effekt auf die Heilung. Verringerter Blutdruck hat einen positiven Einfluss auf die Heilung. Sucht man innerhalb der Leute mit gesenktem Blutdruck nach Effekten, findet man nur den toxischen Effekt: Gegeben diesen Blutdruck ist das Medikament schädlich aufgrund des toxischen Effekts. Der positive Effekt der Blutdruck-Senkung ist auf diese Art nicht zu sehen.

Das Kausalmodell von Studie B ist in Abbildung 11.2 dargestellt.

Abbildung 11.2: Drug hat keinen direkten, aber zwei indirekte Effekt auf recovery, einer davon ist heilsam, einer schädlich

Betrachtung der Teildaten zeigt nur den toxischen Effekt des Medikaments, nicht den nützlichen (Reduktion des Blutdrucks).

Wichtig

Betrachtung der Gesamtdaten zeigt in diesem Fall den wahren, kausalen Effekt. Stratifizieren wäre falsch, da dann nur der toxische Effekt, aber nicht der heilsame Effekt sichtbar wäre.

11.2.3 Studie A und B: Gleiche Daten, unterschiedliches Kausalmodell

Vergleichen Sie die DAGs Abbildung 11.1 und Abbildung 11.2, die die Kausalmodelle der Studien A und B darstellen: Sie sind unterschiedlich. Aber: Die Daten sind identisch.

Kausale Interpretation - und damit Entscheidungen für Handlungen - war nur möglich, da das Kausalmodell bekannt ist. Die Daten alleine reichen nicht. Gut merken.

11.2.4 Sorry, Statistik: Du allein schaffst es nicht

Statistik alleine reicht nicht für Kausalschlüsse. 🧟

Statistik plus Theorie erlaubt Kausalschlüsse. 📚➕📊 🟰 🤩

Wichtig

Für Entscheidungen (“Was soll ich tun?”) braucht man kausales Wissen. Kausales Wissen basiert auf einer Theorie (Kausalmodell) plus Daten.

11.2.5 Vertiefung³

11.2.5.1 Studie C: Nierensteine

Nehmen wir an, es gibt zwei Behandlungsvarianten bei Nierensteinen, Behandlung A und B. Ärzte tendieren zu Behandlung A bei großen Steinen (die einen schwereren Verlauf haben); bei kleineren Steinen tendieren die Ärzte zu Behandlung B.

Sollte ein Patient, der nicht weiß, ob sein Nierenstein groß oder klein ist, die Wirksamkeit in der Gesamtpopulation (Gesamtdaten) oder in den stratifizierten Daten (Teildaten nach Steingröße) betrachten, um zu entscheiden, welche Behandlungsvariante er (oder sie) wählt?

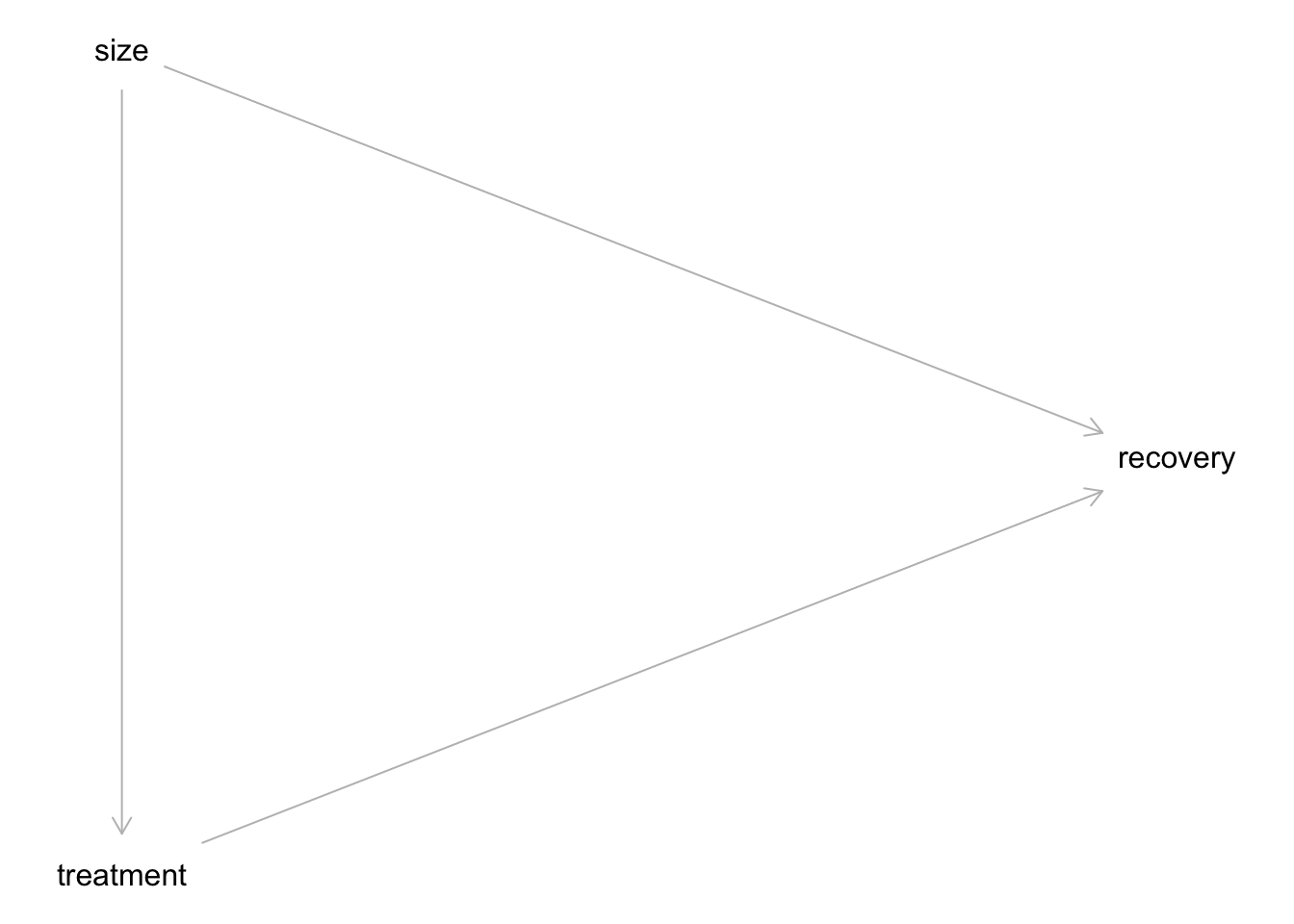
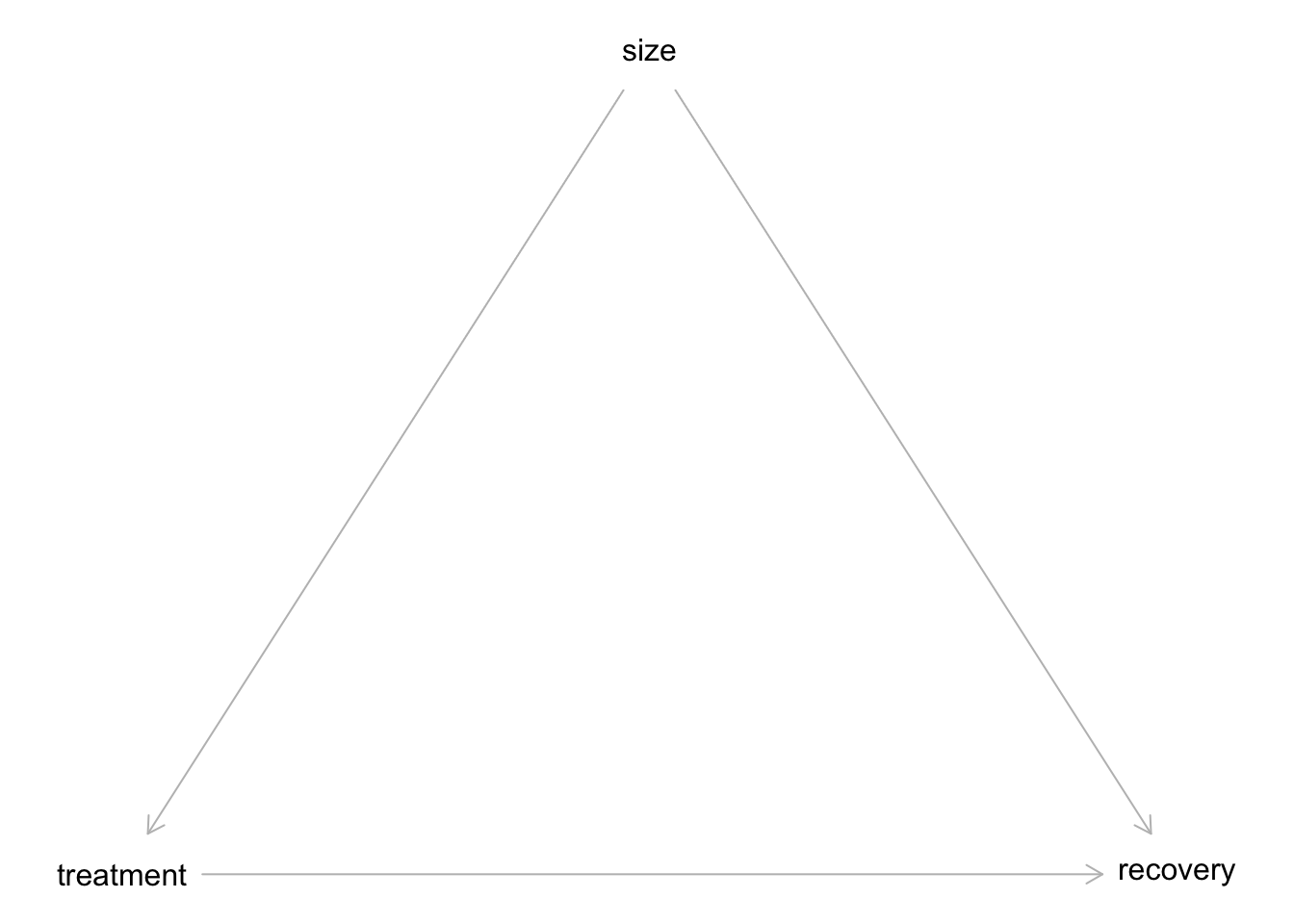
Die Größe der Nierensteine hat einen Einfluss auf die Behandlungsmethode. Die Behandlung hat einen Einfluss auf die Heilung. Damit gibt es eine Mediation (“Kette”) von Größe \(\rightarrow\) Behandlung \(\rightarrow\) Heilung. Darüber hinaus gibt es noch einen Einfluss von Größe der Nierensteine auf die Heilung.

Das Kausalmodell ist in Abbildung 11.3 dargestellt; Abbildung 11.4 visualisiert alternativ. Beide Varianten zeigen das Gleiche. Sie können sich einen aussuchen. Hier sind beide Varianten gezeigt, damit Sie wissen, dass verschiedene Darstellungsformen möglich sind.

Sollte man hier size kontrollieren, wenn man den Kausaleffekt von treatment schätzen möchte? Oder lieber nicht kontrollieren?

DAG links-rechts

Abbildung 11.3: DAG zur Nierenstein-Studie

DAG oben-unten

Abbildung 11.4: DAG zur Nierenstein-Studie in zweiter Darstellungsform

Ja: In diesem Fall sollte man size kontrollieren, denn man ist am Effekt des treatments interessiert. Würde man nicht size kontrollieren, bekäme man den “vermengten” Effekt von size und treatment, also keine (belastbare) Aussage über den Effekt der Behandlung.

11.2.5.2 Mehr Beispiele

Beispiel 11.1 Studien zeigen, dass Einkommen und Heiraten (bzw. verheiratete sein) hoch korrelieren. Daher wird sich dein Einkommen erhöhen, wenn du heiratest. \(\square\)

Beispiel 11.2 Studien zeigen, dass Leute, die sich beeilen, zu spät zu ihrer Besprechung kommen. Daher lieber nicht beeilen, oder du kommst zu spät zu deiner Besprechung. \(\square\)

11.2.6 Zwischenfazit

Bei Beobachtungsstudien ist aus den Daten alleine nicht herauszulesen, ob eine Intervention wirksam ist, ob es also einen kausalen Effekt von der Intervention (angenommen Ursache) auf eine AV (Wirkung) gibt. Damit ist auch nicht zu erkennen, welche Entscheidung zu treffen ist. Nur Kenntnis des Kausalmodells zusätzlich zu den Daten erlaubt, eine Entscheidung sinnvoll zu treffen.

Bei experimentellen Daten ist die Kenntnis des Kausalmodells nicht nötig (wenn das Experiment handwerklich gut gestaltet ist): Das Randomisieren der Versuchspersonen zu Gruppen und das Kontrollieren der Versuchsbedingungen sorgen dafür, dass es keine Konfundierung gibt.

11.3 Konfundierung

11.3.1 Die Geschichte von Angie und Don

🧑

Don, Immobilienmogul, Auftraggeber

👩

Angie, Data Scientistin.

🧞

Wolfie, Post-Nerd, kommt in dieser Geschichte aber nicht vor

📺 Don und Angie

11.3.2 Datensatz ‘Hauspreise im Saratoga County’

Importieren Sie den Datensatz SaratogaHouses, s. Kapitel 11.1.3.

Tabelle 11.3: Saratoga-County-Datensatz

11.3.3 Immobilienpreise in einer schicken Wohngegend vorhersagen

“Finden Sie den Wert meiner Immobilie heraus! Die Immobilie muss viel wert sein!”

🧑 Das ist Don, Immobilienmogul, Auftraggeber.

Das finde ich heraus. Ich mach das wissenschaftlich.

👩 🔬 Das ist Angie, Data Scientistin.

11.3.4 Modell 1: Preis als Funktion der Anzahl der Zimmer

“Hey Don! Mehr Zimmer, mehr Kohle!” 👩 🔬

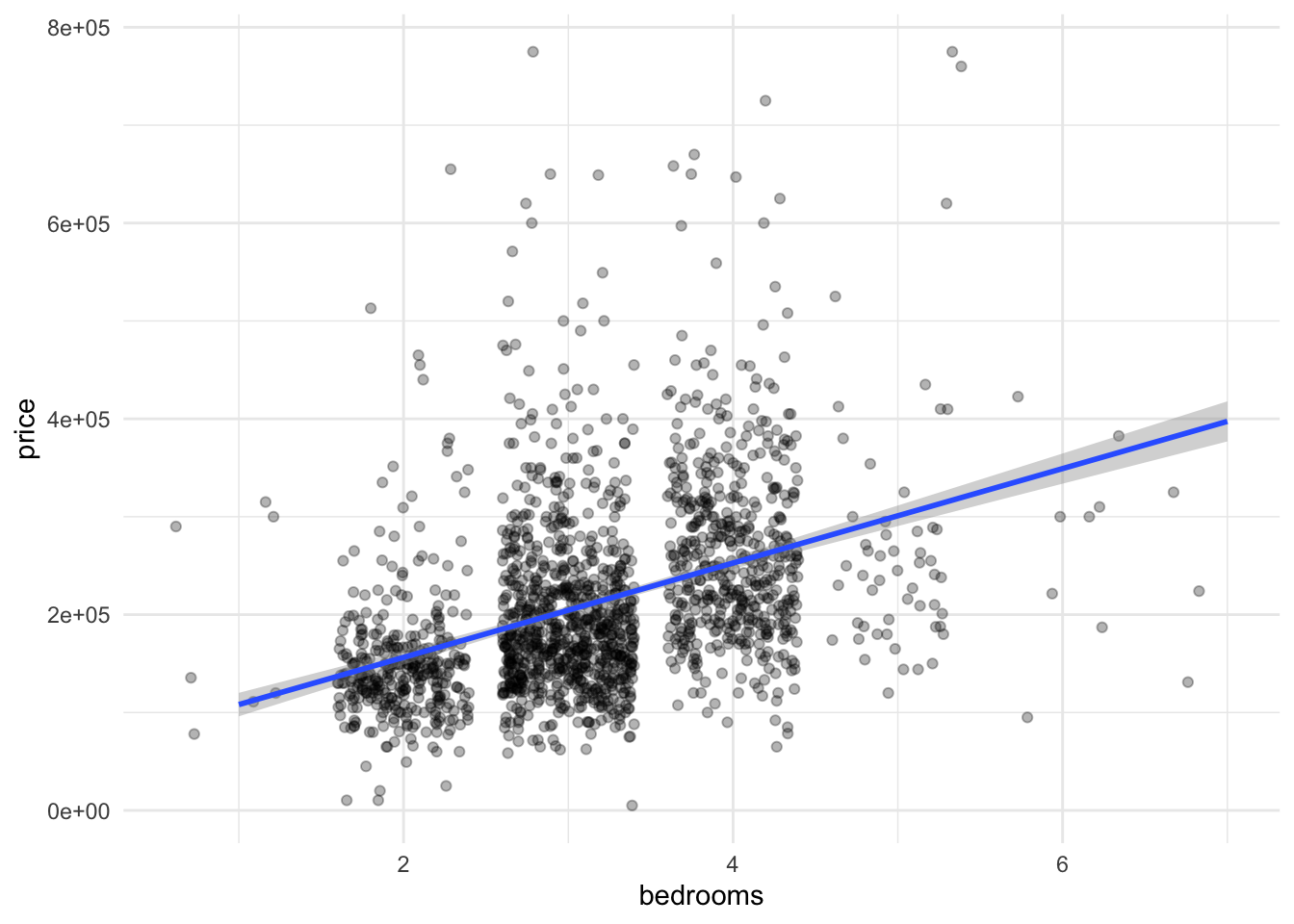
Modell 1 (m1) modelliert den Hauspreis als Funktion der Zimmerzahl, s. Abbildung 11.5.

Abbildung 11.5: Modell m1

“Jedes Zimmer mehr ist knapp 50 Tausend wert. Dein Haus hat einen Wert von etwa 150 Tausend Dollar, Don.”

👩

Zu wenig! 🤬

🧑

Berechnen wir das Modell m1; der Punktschätzer des Parameters bedroom steht in Tabelle 11.4.

m1 <- stan_glm(price ~ bedrooms,
               refresh = 0,
               seed = 42,
               data = d)

point_estimate(m1)

Tabelle 11.4: Parameter für m1

point_estimates(modell) gibt die Punktschätzer der Parameter eines Modells zurück, aber nicht die Schätzbereiche. Möchten Sie beides, können Sie die Funktion parameters(modell) nutzen.⁴

Mit estimate_predictions können wir Vorhersagen berechnen (bzw. schätzen; die Vorhersagen sind ja mit Ungewissheit verbunden, daher ist “schätzen” vielleicht das treffendere Wort). Tabelle 11.5 zeigt den laut m1 vorhergesagten Hauspreis für ein Haus mit 2 Zimmern.

dons_house <- tibble(bedrooms = 2)
estimate_prediction(m1, data = dons_house)

Tabelle 11.5: Vorhersage des Hauspreises für ein Haus mit 2 Zimmern

Model-based Prediction

bedrooms	Predicted	SE	95% CI
2.00	1.53e+05	89682.42	(-21279.13, 3.27e+05)

Variable predicted: price

11.3.5 Don hat eine Idee

“Ich bau eine Mauer! Genial! An die Arbeit, Angie!” 🧑

Don hofft, durch Verdopplung der Zimmerzahl den doppelten Verkaufspreis zu erzielen. Ob das klappt?

“Das ist keine gute Idee, Don.”

👩

Berechnen wir die Vorhersagen für Dons neues Haus (mit den durch Mauern halbierten Zimmern), s. Tabelle 11.6.⁵

dons_new_house <- tibble(bedrooms = 4)
estimate_prediction(m1, dons_new_house)
predict(m1, newdata = dons_new_house)

Tabelle 11.6: Vorhergesagter Hauspreis laut m1 für ein Haus mit 4 Zimmern

Model-based Prediction

bedrooms	Predicted	SE	95% CI
4.00	2.53e+05	89137.61	(79832.69, 4.25e+05)

Variable predicted: price

Mit 4 statt 2 Schlafzimmer steigt der Wert auf 250k, laut m1, s. Abbildung 11.5.

“Volltreffer! Jetzt verdien ich 100 Tausend mehr! 🤑 Ich bin der Größte!” 🧑

Hinweis

Zur Erinnerung: “4e+05” ist die Kurzform der wissenschaftlichen Schreibweise und bedeutet: \(4 \cdot 100000 = 4\cdot10^5 = 400000\)

11.3.6 R-Funktionen, um Beobachtungen vorhersagen

predict(m1, dons_new_house) oder point_estimate(m1, dons_new_house) sagt einen einzelnen Wert vorher (den sog. Punktschätzer der Vorhersage).⁶ Ein Intervall wird nicht ausgegeben.

estimate_prediction(m1, dons_new_house) erstellt Vorhersageintervalle, berücksichtigt also zwei Quellen von Ungewissheit:

• Ungewissheiten in den Parametern (Modellkoeffizienten, \(\beta_0, \beta_1, ...\))
• Ungewissheit im “Strukturmodell”: Wenn also z.B. in unserem Modell ein wichtiger Prädiktor fehlt, so kann die Vorhersagen nicht präzise sein. Fehler im Strukturmodell schlagen sich in breiten Schätzintervallen (bedingt durch ein großes \(\sigma\)) nieder.

estimate_expectation(m1, dons_new_house) erstellt Konfidenzintervalle. berücksichtigt also nur eine Quelle von Ungewissheit:

• Ungewissheiten in den Parametern (Modellkoeffizienten)

Die Schätzbereiche sind in dem Fall deutlich kleiner, s. Tabelle 11.7.

estimate_expectation(m1, dons_new_house)

Tabelle 11.7: Ungewissheit für die Parameter, also die Regressionsgerade, nicht die Beobachtungen

Model-based Expectation

bedrooms	Predicted	SE	95% CI
4.00	2.53e+05	3109.34	(2.47e+05, 2.59e+05)

Variable predicted: price

11.3.7 Modell 2

Berechnen wir das Modell m2: price ~ bedrooms + livingArea. Tabelle 11.8 gibt den Punktschätzer für die Koeffizienten wider.

m2 <- stan_glm(price ~ bedrooms + livingArea, 
               data = d, 
               seed = 42,
               refresh = 0)

point_estimate(m2, centrality = "median")

Tabelle 11.8: Parameter (Punktschätzer, keine Schätzung der Ungewissheit) von m2

Point Estimate

Parameter	Median
(Intercept)	36890.16
bedrooms	-14206.16
livingArea	125.36

Was sind die Vorhersagen des Modell? Tabelle 11.9 gibt Aufschluss für den laut m2 vorhersagten Kaufpreis eines Hauses mit 4 Zimmern und 1200 Quadratfuß Wohnfläche; Tabelle 11.10 gibt die Schätzung (laut m2) für den Preis eines Hauses mit 2 Zimmern (und der gleichen Wohnfläche). Die Vorhersage erhält man mit dem Befehl predict():

predict(m2, newdata = data.frame(bedrooms = 4, livingArea = 1200))
##        1 
## 130369.5

Tabelle 11.9: Vorhersage von m2 für ein Haus mit 4 Zimmern und 1200 Einheiten Wohnfläche

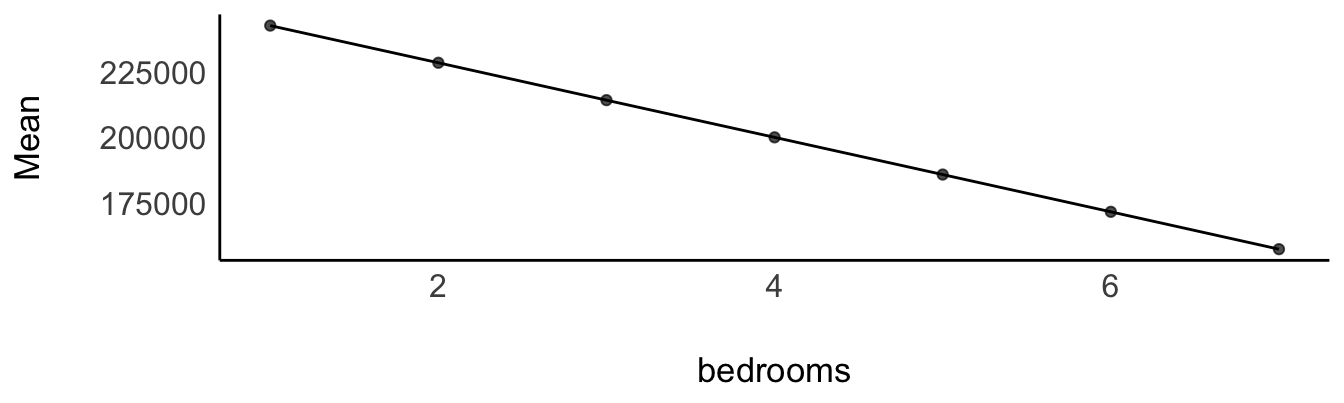
Tabelle 11.10: Vorhersage von m2 für ein Haus mit 2 Zimmern und 1200 Einheiten Wohnfläche

Andere, aber ähnliche Frage: Wieviel kostet ein Haus mit sagen wir 4 Zimmer gemittelt über die verschiedenen Größen von livingArea? Stellen Sie sich alle Häuser mit 4 Zimmern vor (also mit verschiedenen Wohnflächen). Wir möchten nur wissen, was so ein Haus “im Mittel” kostet. Wir möchten also die Mittelwerte pro bedroom schätzen, gemittelt für jeden Wert von bedroom über livingArea. Die Ergebnisse stehen in Tabelle 11.11 und sind in Abbildung 11.6 visualisiert.

estimate_means(m2, at = "bedrooms", length = 7)

Tabelle 11.11: Vorhersagen des Preises von Häusern mit verschiedener Zimmerzahl gemittelt über die verschiedenen Werte der Wohnfläche; basierend auf m2.

Abbildung 11.6: Hauspreis als Funktion der Zimmerzahl, laut m2

“Die Zimmer zu halbieren, hat den Wert des Hauses verringert, Don!”

👩

“Verringert!? Weniger Geld?! Oh nein!”

🧑

11.3.8 Die Zimmerzahl ist negativ mit dem Preis korreliert

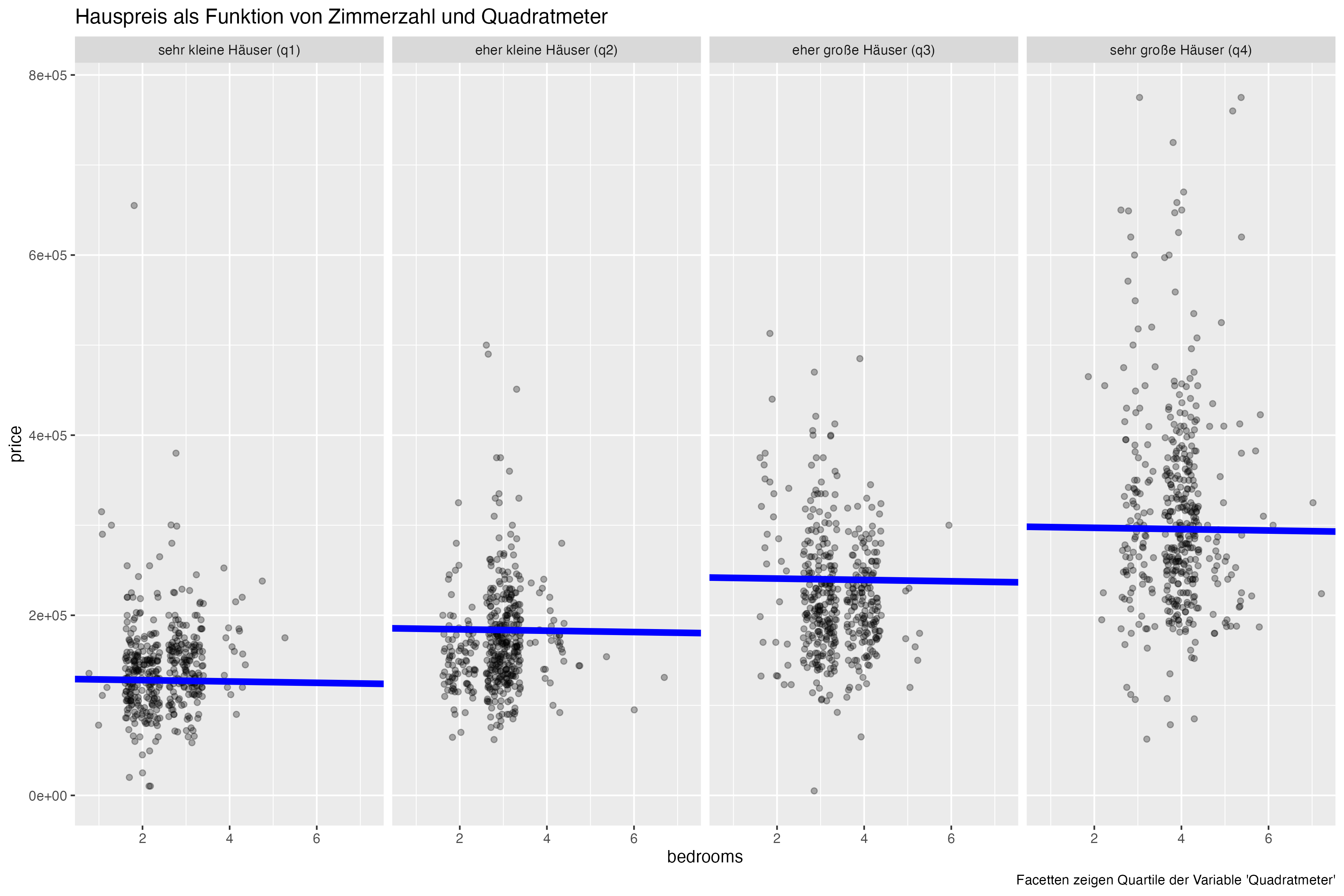
… wenn man die Wohnfläche (Quadratmeter) kontrolliert, s. Abbildung 11.7.

“Ne-Ga-Tiv!”

👩

Abbildung 11.7: Hauspreis stratifizieren

Quellcode

Hinweis

Aussagen, gleich ob sie statistischer, wissenshaftlicher oder sonstiger Couleur sind, können immer nur dann richtig sein, wenn ihre Annahmen richtig sind. Behauptet etwa ein Modell, dass der Wert einer Immobilie steigt, wenn man mehr Zimmer hat, so ist das kein Naturgesetz, sondern eine Aussage, die nur richtig sein kann, wenn das zugrundeliegende Modell richtig ist. \(\square\)

11.3.9 Kontrollieren von Variablen

💡 Durch das Aufnehmen von Prädiktoren in die multiple Regression werden die Prädiktoren kontrolliert (adjustiert, konditioniert):

Die Koeffizienten einer multiplen Regression zeigen den Zusammenhang \(\beta\) des einen Prädiktors mit \(y\), wenn man den (oder die) anderen Prädiktoren statistisch konstant hält.

Man nennt die Koeffizienten einer multiplen Regression daher auch parzielle Regressionskoeffizienten. Manchmal spricht man, eher umgangssprachlich, auch vom “Netto-Effekt” eines Prädiktors, oder davon, dass ein Prädiktor “bereinigt” wurde vom (linearen) Einfluss der anderen Prädiktoren auf \(y\).

Damit kann man die Regressionskoeffizienten so interpretieren, dass Sie den Effekt des Prädiktors \(x_1\) auf \(y\) anzeigen unabhängig vom Effekt der anderen Prädiktoren, \(x_2,x_3,...\) auf \(y\).

Man kann sich dieses Konstanthalten vorstellen als eine Aufteilung in Gruppen: Der Effekt eines Prädiktors \(x_1\) wird für jede Ausprägung (Gruppe) des Prädiktors \(x_2\) berechnet.

Wichtig

Das Hinzufügen von Prädiktoren kann die Gewichte der übrigen Prädiktoren ändern. \(\square\)

Aber welche und wie viele Prädiktoren soll ich denn jetzt in mein Modell aufnehmen?! Und welches Modell ist jetzt richtig?!

🧑

Leider kann die Statistik keine Antwort darauf geben.

👩

Wozu ist sie dann gut?!

🧑

Wichtig

In Beobachtungsstudien hilft nur ein (korrektes) Kausalmodell. Ohne Kausalmodell ist es nutzlos, die Regressionskoeffizienten (oder eine andere Statistik) zur Erklärung der Ursachen heranzuziehen: Die Regressionskoeffizienten können sich wild ändern, wenn man Prädiktoren hinzufügt oder weglässt. Es können sich sogar die Vorzeichen der Regressionsgewichte ändern; in dem Fall spricht man von einem Simpson-Paradox.

11.3.10 Welches Modell richtig ist, kann die Statistik nicht sagen

Often people want statistical modeling to do things that statical modeling cannot do. For example, we’d like to know wheter an effect is “real” or rather spurios. Unfortunately, modeling merely quantifies uncertainty in the precise way that the model understands the problem. Usually answers to lage world questions about truth and causation depend upon information not included in the model. For example, any observed correlation between an outcome and predictor could be eliminated or reversed once another predictor is added to the model. But if we cannot think of the right variable, we might never notice. Therefore all statical models are vulnerable to and demand critique, regardless of the precision of their estimates and apparaent accuracy of their predictions. Rounds of model criticism and revision embody the real tests of scientific hypotheses. A true hypothesis will pass and fail many statistical “tests” on its way to acceptance.

– McElreath (2020), S. 139

11.3.11 Kausalmodell für Konfundierung, km1

Das Kausalmodell km1 ist in Abbildung 11.8 dargestellt; vgl. Abbildung 11.7.

Abbildung 11.8: Kausalmodell km1 - Eine Erklärung (von mehreren) für m1 bzw. die Daten, die m1 zugrunde liegen

Wenn dieses Kausalmodell stimmt, findet man eine Scheinkorrelation zwischen price und bedrooms. Eine Scheinkorrelation ist ein Zusammenhang, der nicht auf eine kausalen Einfluss beruht. d_connected heißt, dass die betreffenden Variablen “verbunden” sind durch einen gerichteten (d wie directed) Pfad, durch den die Assoziation (Korrelation) wie durch einen Fluss fließt 🌊. d_separated heißt, dass sie nicht d_connected sind.

11.3.12 m2 kontrolliert die Konfundierungsvariable livingArea

Beispiel 11.3 In Abbildung 11.8 ist living area eine Konfundierungsvariable für den Zusammenhang von bedrooms und price. \(\square\)

Definition 11.1 (Konfundierungsvariable) Eine Konfundierungsvariable (Konfundierer) ist eine Variable, die den Zusammenhang zwischen UV und AV verzerrt, wenn sie nicht kontrolliert wird (VanderWeele & Shpitser, 2013). \(\square\)

Wenn das Kausalmodell stimmt, dann zeigt m2 den kausalen Effekt von livingArea.

Was tun wir jetzt bloß?! Oh jeh!

🧑

Wir müssen die Konfundierungsvariable kontrollieren.

👩

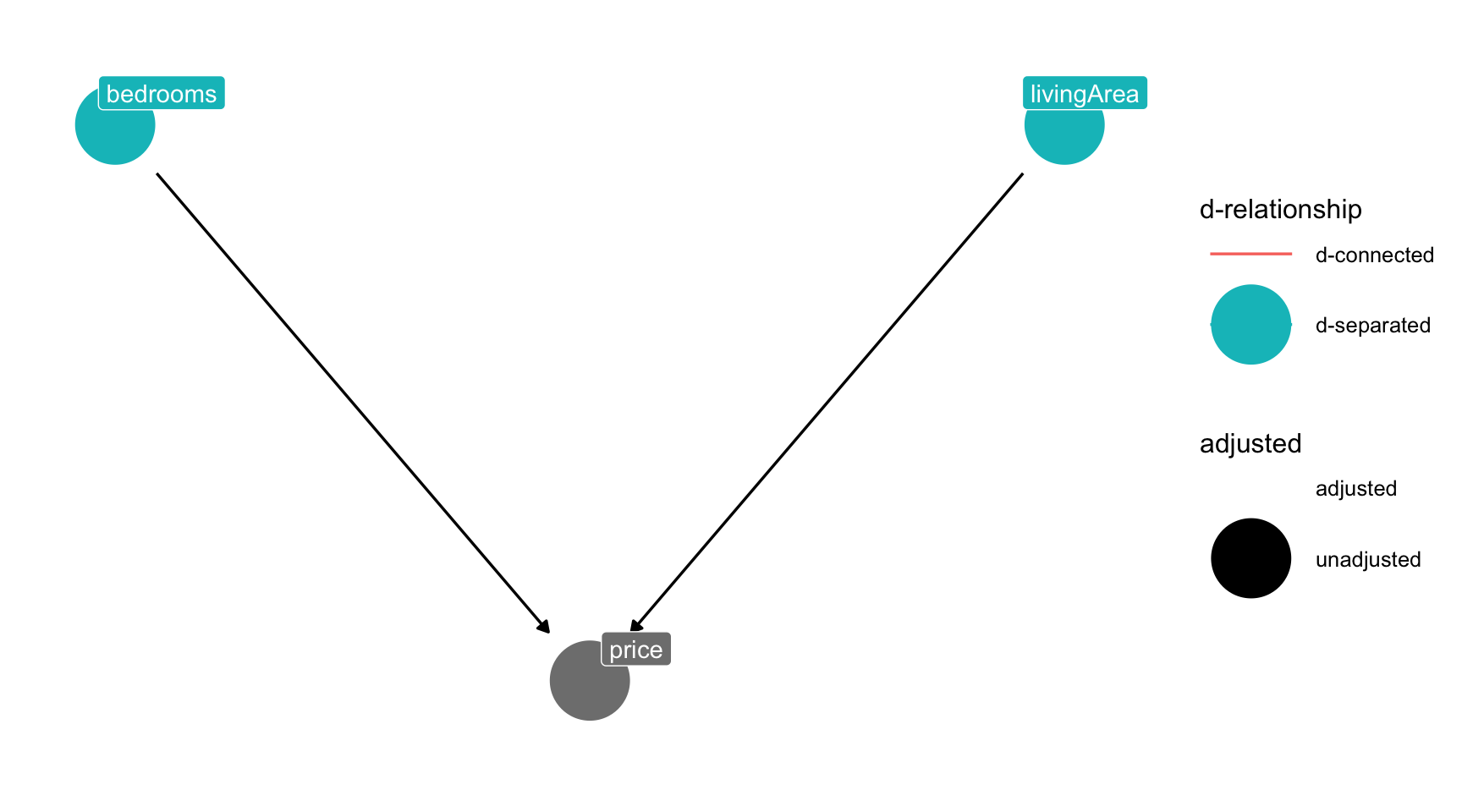
Abbildung 11.9 zeigt, dass bedrooms und price unkorreliert werden (d_separated), wenn man living area kontrolliert.

Abbildung 11.9: Durch Kontrolle von living area wird die Assoziation von price und bedrooms aufgehoben.

Durch das Kontrollieren (“adjustieren”), sind bedrooms und price nicht mehr korreliert, nicht mehr d_connected, sondern jetzt d_separated.

Definition 11.2 (Blockieren) Das Kontrollieren eines Konfundierers (wie living_area) “blockt” den betreffenden Pfad, führt also dazu, dass über diesen Pfad keine Assoziation (z.B. Korrelation) zwischwen UV (bedrooms) und AV (price) mehr vorhanden ist. UV und AV sind dann d_separated (“getrennt”). \(\square\)

11.3.13 Konfundierer kontrollieren

Gehen wir in diesem Abschnitt davon aus, dass km1 richtig ist.

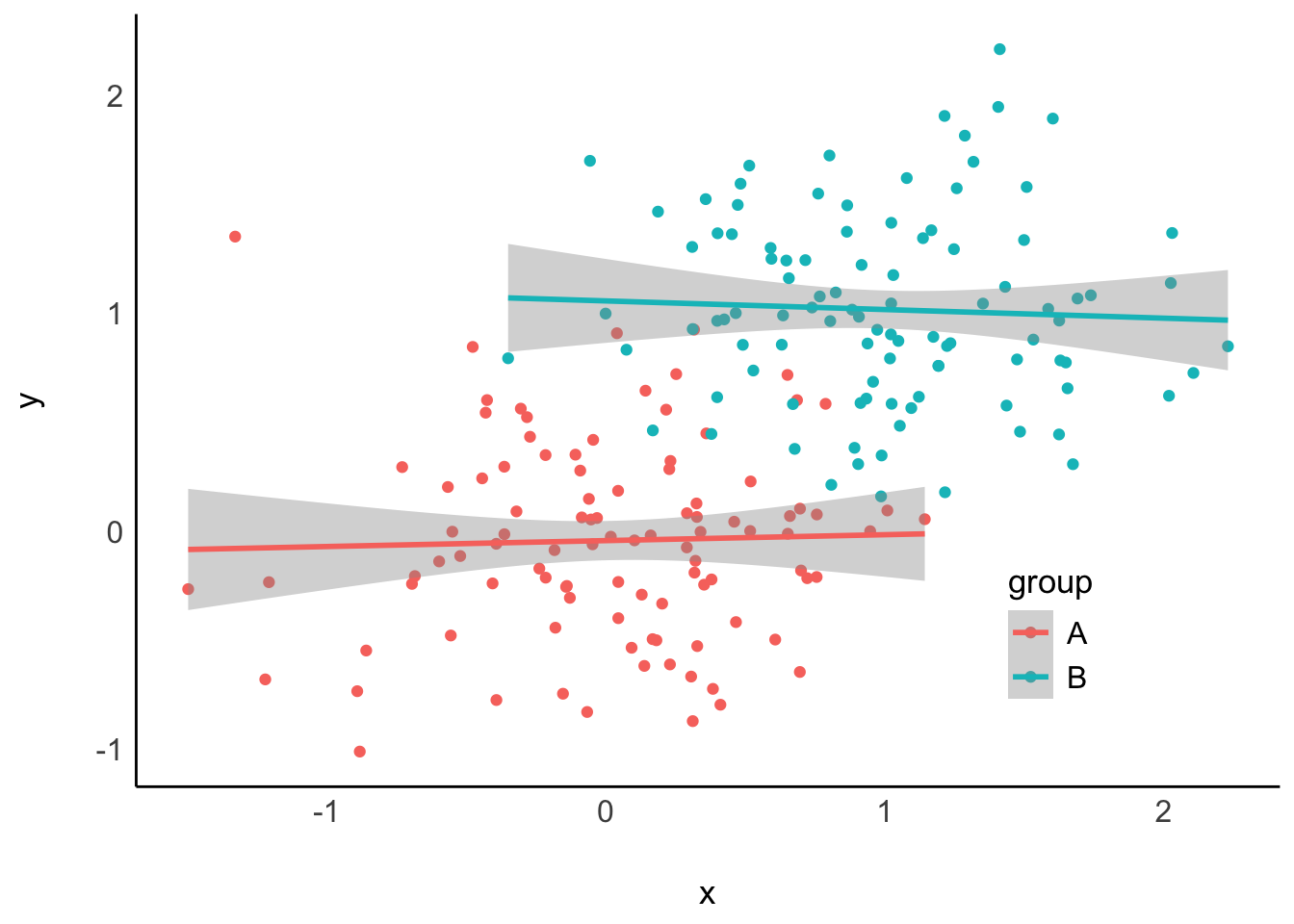
Ohne Kontrollieren der Konfundierungsvariablen: Regressionsmodell y ~ x, Abbildung 11.10, links: Es wird (fälschlich) eine Korrelation zwischen x und y angezeigt: Scheinkorrelation. Mit Kontrollieren der Konfundierungsvariablen: Regressionsmodell y ~ x + group, Abbildung 11.10, rechts.

(a) Ohne Kontrolle der Konfundierungsvariablen: Konfundierung tritt auf.

(b) Mit Kontrolle der Konfundierungsvariablen: Konfundierung tritt nicht auf.

Abbildung 11.10: Konfundierung von y und x!

Abbildung 11.10, rechts, zeigt korrekt, dass es keine Korrelation zwischen x und y gibt, wenn group kontrolliert wird. Außerdem sieht man im rechten Teildiagramm, dass es ein Kontrollieren der Variable group durch Aufnahme als Prädiktor in die Regressionsgleichung einem Stratifizieren entspricht (getrennte Berechnung der Regressionsgerade pro Gruppe).

Wichtig

Kontrollieren Sie Konfundierer. \(\square\)

11.3.14 m1 und m2 passen nicht zu den Daten, wenn km1 stimmt

Laut km1 dürfte es keine Assoziation (Korrelation) zwischen bedrooms und price geben, wenn man livingArea kontrolliert, wie in Abbildung 11.8 dargestellt. Es gibt aber noch eine Assoziation zwischen bedrooms und price geben, wenn man livingArea kontrolliert. Daher sind sowohl m1 und m2 nicht mit dem Kausalmodell km1 vereinbar.

11.3.15 Kausalmodell 2, km2

Unser Modell m2 sagt uns, dass beide Prädiktoren jeweils einen eigenen Beitrag zur Erklärung der AV haben.

Daher könnte das folgende Kausalmodell, km2 besser passen.

In diesem Modell gibt es eine Wirkkette: \(a \rightarrow b \rightarrow p\).

Insgesamt gibt es zwei Kausaleinflüsse von a auf p: - \(a \rightarrow p\) - \(a \rightarrow b \rightarrow p\)

Man nennt die mittlere Variable einer Wirkkette auch einen Mediator und den Pfad von der UV (a) über den Mediator (b) zur AV (p) auch Mediation, s. Abbildung 11.11.

Abbildung 11.11: Der Effekt von livingArea wird über den Mediator bedrooms auf price vermittelt.

11.3.16 Dons Kausalmodell, km3

So sieht Dons Kausalmodell aus, s. Abbildung 11.12.

Abbildung 11.12: Dons Kausalmodell

“Ich glaube aber an mein Kausalmodell. Mein Kausalmodell ist das größte! Alle anderen Kausalmodelle sind ein Disaster!”

🧑

“Don, nach deinem Kausalmodell müssten bedrooms und livingArea unkorreliert sein. Sind sie aber nicht.”

🧑

Rechne doch selber die Korrelation aus, Don:

“Äh, wie ging das nochmal?”

🧑

So könntest du das rechnen, Don: correlation(d, select = c("bedrooms", "livingArea")). Oder z.B. so:

dons_r <- d %>% 
  summarise(cor(bedrooms, livingArea))

Die Korrelation liegt also bei 0.66

“Bitte, gerne hab ich dir geholfen, Don.”

👩

11.3.17 Unabhängigkeiten laut der Kausalmodelle

km1: b: bedrooms, p: price, a area (living area), s. Abbildung 11.8.

Das Kausalmodell km1 behauptet: \(b \perp \!\!\! \perp p \, |\, a\): bedrooms sind unabhängig von price, wenn man livingArea kontrolliert.

Kontrollieren einer Variable \(Z\) erreicht man auf einfache Art, indem man sie in zusätzlich zur vermuteten Ursache \(X\) in die Regressionsgleichung mit aufnimmt, also y ~ x + z.

Aber diese behauptete Unabhängigkeit findet sich nicht in den Daten wieder, s. Tabelle 11.8. Also: ⛈️ Passt nicht zu den Daten!

km2 b: bedrooms, p: price, a area (living area), s. Abbildung 11.11.

Das Kausalmodell km2 postuliert keine Unabhängigkeiten: Laut km2sind alle Variablen des Modells miteinander assoziiert (korreliert).

Hinweis

Ein Modell, in dem alle Variablen miteinander korreliert sind, nennt man auch satuiert oder saturiertes Modell. So ein Modell ist empirisch schwach. Denn: Behauptet ein Modell, dass die Korrelation zwischen zwei Variablen irgendeinen Wert zwischen -1 und +1 beträgt (nur nicht exakt Null), so ist das eine sehr schwache Aussage (und kaum zu falsifizieren). So ein Modell ist wissenschaftlich wenig wert. Das ist so ähnlich wie ein Modell, das voraussagt, dass es morgen irgendeine Temperatur hat zwischen -30 und +30 Grad (nur nicht exakt Null). Trifft diese Temperaturvorhersage ein, so werden wir nicht gerade beeindruckt sein. 🥱

Fazit: km2 passt zu den Daten, aber wir sind nicht gerade beeindruckt vom Modell.

km3: b: bedrooms, p: price, a area (living area), s. Abbildung 11.12.

\(b \perp \!\!\! \perp a\): bedrooms sind unabhängig von livingArea (a)

⛈️ km3 passt nicht zu den Daten/zum Modell!

11.4 DAGs: Directed Acyclic Graphs

Was sind DAGs? Wir haben in diesem Kapitel schon viele Beispiele gesehen, z.B. Abbildung 11.12.

Definition 11.3 (DAG) DAGs sind eine bestimmte Art von Graphen zur Analyse von Kausalstrukturen. Ein Graph besteht aus Knoten (Variablen) und Kanten (Linien), die die Knoten verbinden. DAGs sind gerichtet; die Pfeile zeigen immer in eine Richtung (und zwar von Ursache zu Wirkung). DAGs sind azyklisch; die Wirkung eines Knoten darf nicht wieder auf ihn zurückführen. \(\square\)

Definition 11.4 (Pfad) Ein Pfad ist ein Weg durch den DAG, von Knoten zu Knoten über die Kanten, unabhängig von der Pfeilrichtung. \(\square\)

Der DAG von km1 ist in Abbildung 11.8 zu sehen.

11.4.1 Leider passen potenziell viele DAGs zu einer Datenlage

Auf Basis der in Dons Modell dargestellten (Un-)Abhängigkeiten der Variablen sind noch weitere Kausalmodelle möglich.

In Abbildung 11.13 sind diesen weiteren, möglichen Kausalmodelle für Dons Modell dargestellt. Dabei sind folgende Abkürzungen verwendet: b: bedrooms, p: price, a area (living area).

Ja, der Job der Wissenschaft ist kein Zuckerschlecken. Aber wenn es einfach wäre, die Kausalstruktur der Phänomene zu entdecken, wären sie längst erkannt, und alle Probleme der Menschheit gelöst.

Abbildung 11.13: Kausalmodelle, die potenziell geeignet sind für Dons Fragestellung

Alle diese DAgs in Abbildung 11.8 haben die gleichen Implikationen hinsichtlich der (Un-)Abhängigkeiten zwischen der Variablen. Wir können also leider empirisch nicht bestimmen, welcher der DAGs der richtige ist. Um den richtigen DAG zu identifizieren, bräuchten wir z.B. einen reichhaltigeren DAG, also mit mehr Variablen.

11.4.2 Was ist eigentlich eine Ursache?

Etwas verursachen kann man auch (hochtrabend) als “Kausation” bezeichnen.

Hinweis

Weiß man, was die Wirkung \(W\) einer Handlung \(H\) (Intervention) ist, so hat man \(H\) als Ursache von \(W\) erkannt (McElreath, 2020). \(\square\)

Definition 11.5 (Kausale Abhängigkeit) Ist \(X\) die Ursache von \(Y\), so hängt \(Y\) von \(X\) ab: \(Y\) ist (kausal) abhängig von \(X\). \(\square\)

Viele Menschen denken - fälschlich - dass Korrelation Kausation bedeuten muss, s. Abbildung 11.14.

Abbildung 11.14: xkcd zum Thema Kausation

Quelle und Erklärung

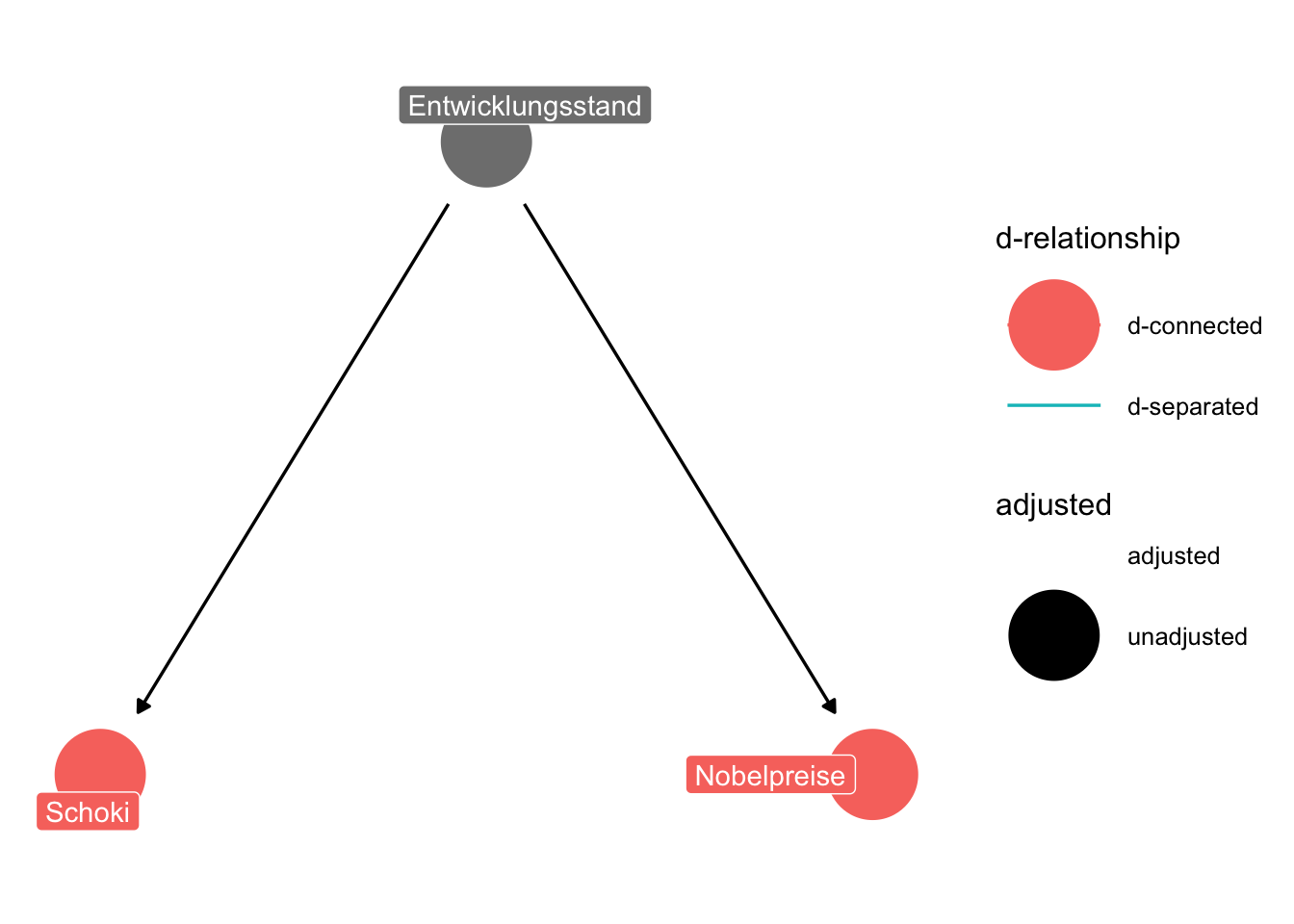
Beispiel 11.4 (Der Schoki-Dag) Der “Schoki-DAG” in Abbildung 11.15 zeigt den DAG für das Schokoloaden-Nobelpreis-Modell. \(\square\)

Abbildung 11.15: Macht Schokolade Nobelpreise?

11.5 Fazit

11.5.1 Zusammenfassung

Sind zwei Variablen korreliert (abhängig, assoziiert), so kann es dafür zwei Gründe geben:

1. Kausaler (“echter”) Zusammenhang
2. Nichtkausaler Zusammenhang (“Scheinkorrelation”)

Man ist daran interessiert, echten (also kausalen) Zusammenhang aufzudecken⁷ und Scheinkorrelation auszuschließen.

Eine von zwei möglichen Ursachen einer Scheinkorrelation ist Konfundierung.⁸

Konfundierung kann man aufdecken, indem man die angenommene Konfundierungsvariable kontrolliert (adjustiert), z.B. indem man ihn als Prädiktor in eine Regression aufnimmt.

Ist die Annahme einer Konfundierung korrekt, so löst sich der Scheinzusammenhang nach dem Adjustieren auf.

Löst sich der Scheinzusammenhang nicht auf, sondern drehen sich die Vorzeichen der Zusammenhänge nach Adjustieren um, so spricht man einem Simpson-Paradox.

Die Daten alleine können nie sagen, welches Kausalmodell der Fall ist in einer Beobachtungsstudie. Fachwissen (inhaltliches wissenschaftliches Wissen) ist nötig, um DAGs auszuschließen.

11.5.2 Ausstieg

Beispiel 11.5 (Schoki macht Nobelpreis!?) Eine Studie fand eine starke Korrelation, \(r=0.79\) zwischen der Höhe des Schokoladenkonsums eines Landes und der Anzahl der Nobelpreise eines Landes (Messerli, 2012), s. Abbildung 11.16.

Abbildung 11.16: Je mehr Schoki, desto mehr Nobelpreise

Wichtig

Korrelation ungleich Kausation! Korrelation kann bedeuten, dass eine Kausation vorliegt, aber es muss auch nicht sein, dass Kausation vorliegt. Liegt Korrelation ohne Kausation vor, so spricht man von einer Scheinkorrelation. Um Scheinkorrelation von echter Assoziation (auf Basis von Kausation) abzugrenzen, muss man die Kausalmodelle überprüfen, so wie wir das hier tun.

11.5.3 Vertiefung

Es gibt viel Literatur zu dem Thema Kausalinferenz. Ein Artikel, der einen vertieften Einblick in das Thema Konfundierung liefert z.B. Tennant et al. (2020) oder Suttorp et al. (2015). Allerdings sollte man neben Konfundierung noch die drei anderen “Atome” der Kausalinferenz - Kollision, Mediation (und Nachfahre) - kennen, um gängige Fragen der Kausalinferenz bearbeiten zu können.

11.6 Aufgaben

• Sammlung “kausal”

11.7 —

McElreath, R. (2020). Statistical Rethinking: A Bayesian Course with Examples in R and Stan (2. Aufl.). Taylor and Francis, CRC Press.

Messerli, F. H. (2012). Chocolate Consumption, Cognitive Function, and Nobel Laureates. New England Journal of Medicine, 367(16), 1562–1564. https://doi.org/10.1056/NEJMon1211064

Pearl, J., Glymour, M., & Jewell, N. P. (2016). Causal Inference in Statistics: A Primer. Wiley.

Rohrer, J. M. (2018). Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data. Advances in Methods and Practices in Psychological Science, 1(1), 27–42. https://doi.org/10.1177/2515245917745629

Suttorp, M. M., Siegerink, B., Jager, K. J., Zoccali, C., & Dekker, F. W. (2015). Graphical Presentation of Confounding in Directed Acyclic Graphs. Nephrology Dialysis Transplantation, 30(9), 1418–1423. https://doi.org/10.1093/ndt/gfu325

Tennant, P. W. G., Murray, E. J., Arnold, K. F., Berrie, L., Fox, M. P., Gadd, S. C., Harrison, W. J., Keeble, C., Ranker, L. R., Textor, J., Tomova, G. D., Gilthorpe, M. S., & Ellison, G. T. H. (2020). Use of Directed Acyclic Graphs (DAGs) to Identify Confounders in Applied Health Research: Review and Recommendations. International Journal of Epidemiology, 50(2), 620–632. https://doi.org/10.1093/ije/dyaa213

VanderWeele, T. J., & Shpitser, I. (2013). On the Definition of a Confounder. Annals of statistics, 41(1), 196–220. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4276366/

---

1. Nur weil die Variablen Anzahl_Stoerche und Anzahl_Babies korreliert sind, heißt das nicht, dass das eine die Ursache des anderen sein muss.

2. Nein

3. Dieser Abschnitt ist prüfungsrelevant, birgt aber nichts Neues.

4. In aller Regel macht es mehr Sinn, die Schätzbereiche der Punktschätzer auch zu betrachten. Nur die Punktschätzer zu betrachten vernachlässigt wesentliche Information.

5. Anstelle von estimate_relation() kann man auch (einfacher vielleicht) predict() verwenden: predict(m1, newdata = dons_new_house). Allerdings gibt predict() nur den vorhergesagten Wert aus. estimate_prediction() gibt noch zusätzlich das Vorhersageintervall aus, berücksichtigt also die (doppelte) Ungewissheit der Vorhersage. Mit anderen Worten: estimate_prediction gibt die PPV aus.

6. Bei predict ist dieser Wert der Median der Post-Verteilung; bei point_estimate kann man sich aussuchen, ob der Median, der Mittelwert oder der wahrscheinlichste Wert der Post-Verteilung als Schätzwert verwendet wird.

7. zu “identifizieren”

8. Die andere Ursache ist die Kollisionsverzerrung, s. #sec-kausal.