2 Wozu Statistik?
2.1 Lernsteuerung
Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf. Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.
Sie können …
- die drei Zielarten der Statistik nennen und beschreiben können
- die Definition von Inferenzstatistik sowie Beispiele für inferenzstatistische Fragestellungen nennen
- zentrale Begriffe der Inferenzstatistik nennen und in Grundzügen erklären
- den Nutzen von Inferenzstatistik nennen
- erläutern, in welchem Zusammenhang Ungewissheit zur Inferenzstatistik steht
- anhand von Beispielen erklären, was ein statistisches Modell ist
- die Grundkonzepte der Regression angeben
- Unterschiede zwischen frequentistischer (“klassischer”) und Bayes-Inferenz benennen
- Vor- und Nachteile der frequentistischen vs. Bayes-Inferenz diskutieren
- Die grundlegende Herangehensweise zur Berechnung des p-Werts informell erklären
Bei Gelman et al. (2021), Kap. 1 findet sich eine Darstellung ähnlich zu der in diesem Kapitel. Die Begleitliteratur ist nicht prüfungsrelevant; sie dient zur Vertiefung und als Grundlage einer ausführlicheren Erläuterung des Stoffes.
Bereiten Sie sich im Eigenstudium auf dieses Kapitel vor. Lesen Sie dazu folgende Themen:
- Statistik 1, Kap. “Rahmen”
- Statistik 1, dort alle Inhalte aller Kapitel zum Thema “Modellieren” bzw. “Regression”
- Statistik 1, Abschnitt zur Normalverteilung
Diese Begleitvideos helfen Ihnen bei der Vor- und Nachbereitung dieses Kapitels:
📺 Wozu ist Statistik eigentlich da? Diese Frage haben Sie sich auch schon mal gestellt? Abb. Abbildung 2.1 gibt einen Überblick über die drei Zielarten der statistikbasierten wissenschaftlichen Forschung.1 Nach dieser Einteilung lassen sich drei Arten von Zielen unterscheiden: Beschreiben, Vorhersagen und Erklären (Shmueli, 2010).
2.2 Die drei Zielarten der Statistik
2.2.1 Überblick
2.2.1.1 📄 Beschreiben (deskriptiv)
- Wie stark ist der (lineare) Zusammenhang
- Wie stark ist der (lineare) Zusammenhang
- Haben unsere Kunden bisher Webshop A oder B bevorzugt, laut unseren Daten?
2.2.1.2 🔮 Vorhersagen (prädiktiv, prognostisch)
- Wie schwer ist wohl Herr X? Er ist ein deutscher erwachsener Mann der Größe 1,80m; mehr wissen wir nicht.
- Welche Note kann man erwarten, wenn man nichts für die Klausur lernt?
- Wie viel wird ein Kunde ausgeben, wenn er sich in der Variante A des Webshops aufhält?
2.2.1.3 🔗 Erklären
Kausalinferenz:
- Ist Größe eine Ursache von Gewicht (bei deutschen Männern)?
- Wenn ich 100 Stunden lerne, welche Note schreibe ich dann?
Populationsinferenz:
- Wie stark ist der (lineare) Zusammenhang
- Bevorzugen unsere Kunden allgemein Webshop A oder B laut unseren Daten?
Erklärung (Inferenz) ist zumeist das Erkenntnisziel wissenschaftlicher Studien. Anhand der verwendeten statistischen Methode (z.B. Regressionsanalyse) kann man nicht feststellen, zu welchem Erkenntnisziel die Studie gehört. Um das Erkenntnisziel festzustellen, liest man sich die Forschungsfrage oder das Ziel der Studie durch.
Beispiel 2.1 (Beispiele für die Zielarten statistischer Analysen)
- Beschreiben: “Wie groß ist der Gender-Paygap in der Branche X im Zeitraum Y?”
- Vorhersagen: Wenn eine Person, Mr. X, 100 Stunden auf die Statistikklausur lernen, welche Note kann diese Person dann erwarten?
- Erklären: Wie viel bringt (mir) das Lernen auf die Statistikklausur?
Für die Wissenschaft ist Erklären das wichtigste Ziel. Bei wenig beackerten Wissenschaftsfeldern ist das Beschreiben ein sinnvoller erster Schritt. Vorhersagen ist mehr für die Praxis als für die Wissenschaft relevant.
2.2.2 Zielart Beschreiben
Statistische Analysen mit dem Ziel zu beschreiben fassen die Daten zusammen (zu möglichst aussagekräftigen Kennzahlen). Beschreibende Statistik nennt man auch deskriptive Statistik; Mittelwert, Korrelation und Regressionskoeffizienten sind typische Kennzahlen (“Statistiken”); s. Abbildung 2.2.
Der beschreibenden Statistik geht es nicht darum, Erkenntnisse zu ziehen, die über die Daten hinaus gehen. So ist man in der beschreibenden Statistik nicht daran interessiert, Aussagen über die zugrundeliegende Population anzustellen.
Beispiel 2.2 In einem Hörsaal sitzen 100 Studis. Alle schreiben Ihre Körpergröße auf einen Zettel. Die Dozentin sammelt die Zettel ein und rechnet dann den Mittelwert der Körpergröße der anwesenden Studentis aus. Voilà: Deskriptive Statistik!
Definition 2.1 (Deskriptivstatistik) Deskriptivstastistik fasst Merkmale aus einer Stichprobe zu Kennzahlen (Statistiken) zusammen.
2.2.3 Zielart Vorhersagen
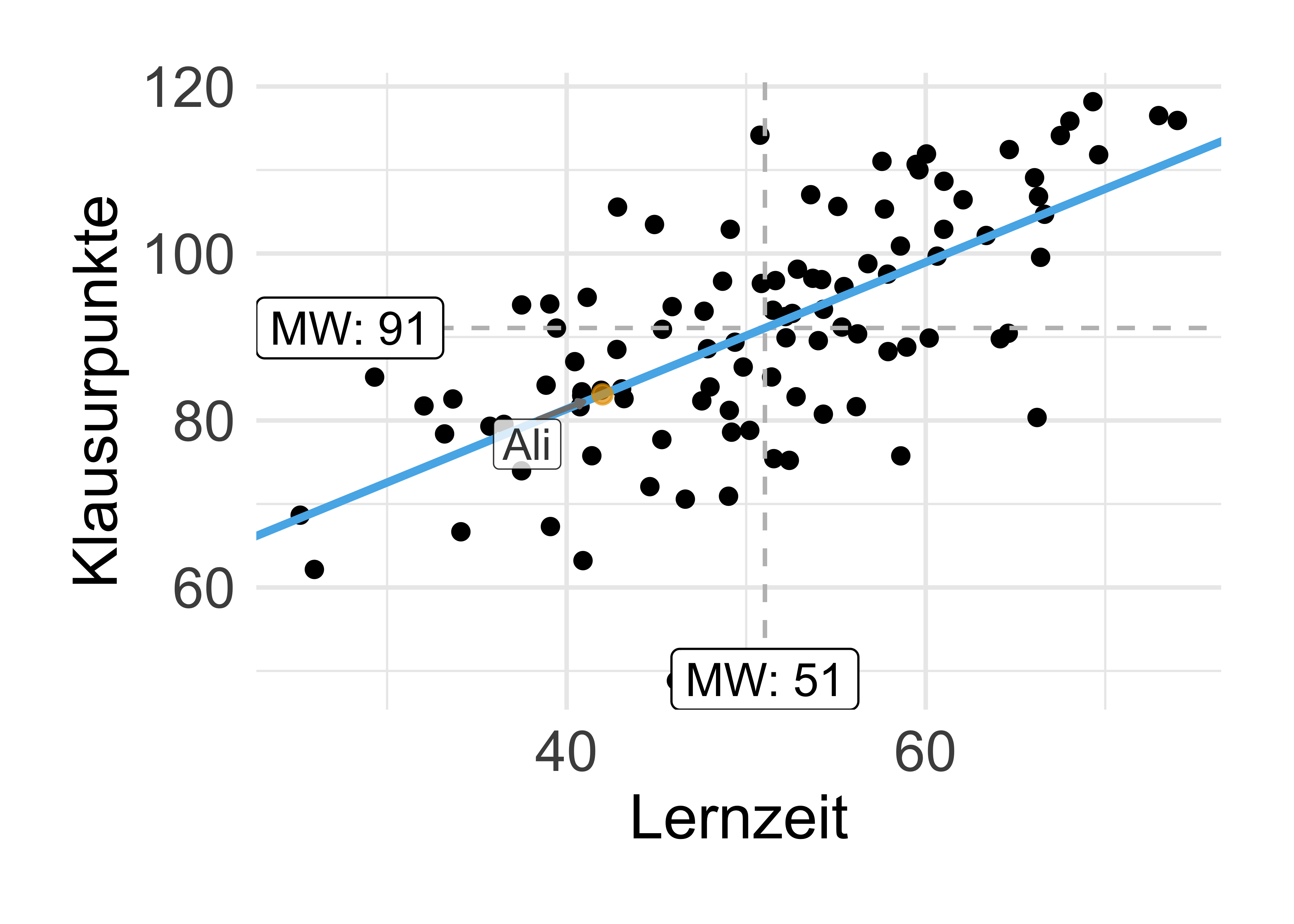
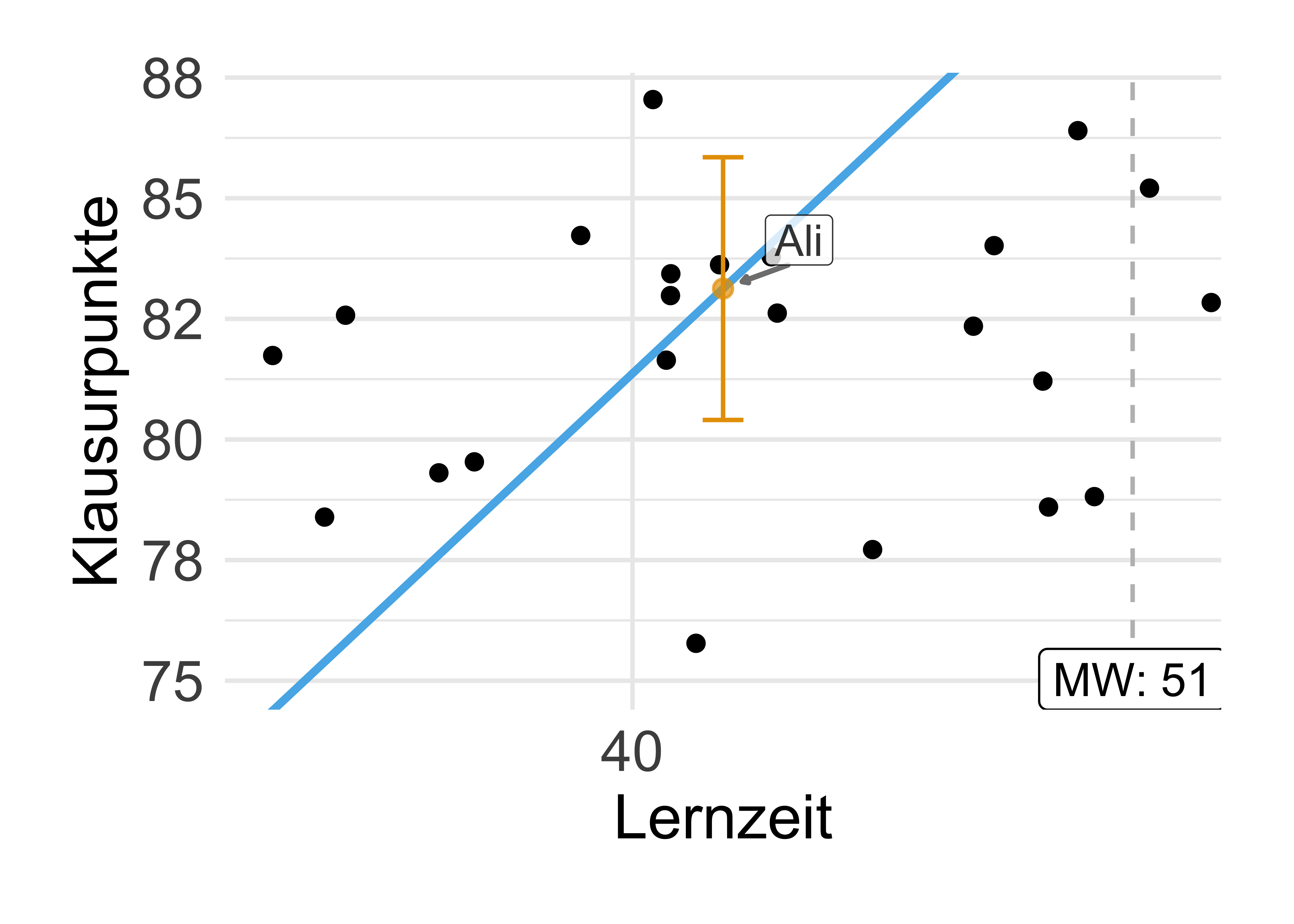
Beim Vorhersagen versucht man, auf Basis von Daten, gegeben bestimmter Werte der UV den Wert einer AV vorherzusagen, s. Abbildung 2.3.
Beispiel 2.3 (Ali lernt für die Klausur) Oh nein, die Klausur im Fach Statistik steht an. Ali lernt ziemlich viel. Wie viel Punkte (von 100 möglichen) wird er wohl erzielen? Ziehen wir ein einfaches statistisches Modell zur Rate, um eine Vorhersage für den “Klausurerfolg” von Ali zu erhalten. Wir können vom Modell eine einzelne Zahl (83) als Punkt-Schätzwert bzw. Vorhersagewert erhalten oder einen Schätzbereich (80-86 Punkte).
Hier ist das Regressionsmodell für Ali (lm_toni), s. Listing 2.1.
2.2.4 Zielart Erklären – Populationsinferenz
Populationsinferenz ist das Schließen von der Stichprobe auf die Grundgesamtheit
Statistische Populationsinferenz – meist kurz als Inferenz bezeichnet – hat zum Ziel, vom Teil aufs Ganze zu schließen, bzw. vom Konkreten auf das Abstrakte. In der Datenanalyse heißt das: Was sagt meine Datensatz, der auf einer Stichprobe beruht, über die zugrundeliegende Grundgesamtheit aus?
Typischerweise untersuchen im Rahmen einer statistischen Analyse eine Stichprobe, wie z.B. Ihr Freundeskreis, der leichtsinnig genug war, auf Ihre WhatsApp-Nachricht “Tolle Studie zu dem Geheimnis des Glücks!!!” zu klicken. Ihr Freundeskreis ist ein Teil der Menschen (z.B. aus Deutschland), also eine Stichprobe. Schauen wir uns den Unterschied zwischen Stichprobe und Population näher an.
Stichprobe vs. Population
Nehmen wir an, wir möchten herausfinden, wie groß der Anteil der R-Fans in der Grundgesamthit (synonym: Population) aller Studierenden ist. Den Anteil der F-Fans bezeichnen wir der Einfachheit halber hier mit A2.
Das Grundproblem der Inferenzstatistik ist, dass wir an Aussagen zur Grundgesamtheit interessiert sind, aber nur eine Stichprobe, also einen Ausschnitt oder eine Teilmenge der Grundgesamtheit (synonym: Population) vorliegen haben.
Wir müssen also den Anteil der R-Fans in der Population auf Basis des Anteils in der Stichprobe schließen: Wir verallgemeinern oder generalisieren von der Stichprobe auf die Grundgesamtheit, s. Abb. Abbildung 2.4.
Häufig ist das praktische Vorgehen recht simpel: Ah, in unserer Stichprobe sind 42% R-Fans!3. Man schreibt: p wie proportion, engl. für “Anteil”). Die Stichprobe sei repräsentativ für die Grundgesamtheit aller Studierender. Messerscharf schließen wir: In der Grundgesamtheit ist der Anteil der R-Fans auch 42%,
Wir verwenden lateinische Buchstaben (p), um Kennzahlen einer Stichprobe zu benennen, und griechische (
Definition 2.2 ((Populations-)Inferenzstatistik) Populations-Inferenzstatistik – meist kurz als Inferenzstatistik bezeichnet – ist ein Verfahren zum Schließen von Statistiken (eine Kennzahl einer Stichprobe) auf Parameter (eine Kennzahl einer Grundgesamtheit). Inferenz bedeutet Schließen bzw. Schlussfolgern: auf Basis von vorliegenden Wissen wird neues Wissen generiert. Inferenzstatistik ist ein Verfahren, das mathematische Modelle (oft aus der Stochastik) verwendet, um ausgehend von einer bestimmten Datenlage auf allgemeine Aussagen zu schließen. Wir unterscheiden zwei Hauptarten der Inferenzstatistik: 1. Populationsinferenz, 2. Kausalinferenz
Übungsaufgabe 2.1 🏋️️ Heute Nacht vor dem Schlafen wiederholen Sie die Definition . Üben Sie jetzt schon mal.
Für jede beliebige Statistik (Kennzahl von Stichprobendaten) kann man die Methoden der Populationsinferenz verwenden, um den zugehörigen Kennwert (Parameter) der Population zu bestimmen, s. Tabelle Tabelle 2.1. Da man die Parameter der Population so gut wie nie sicher kennt (schließlich hat man meist nur Auszüge, Teile der Population, also Stichproben), muss man sich mit Schätzwerten begnügen.
Für Statistiken (Daten einer Stichprobe) verwendet man lateinische Buchstaben; für Parameter (Population) verwendet man griechische Buchstaben.
Übungsaufgabe 2.2 🏋️ Geben Sie die griechischen Buchstaben für typische Statistiken an. Ohne auf die Tabelle zu schauen.😜
Meist begnügt man sich beim Analysieren von Daten nicht mit Aussagen für eine Stichprobe, sondern will auf eine Grundgesamtheit verallgemeinern.
Leider sind die Parameter einer Grundgesamtheit zumeist unbekannt, daher muss man sich mit Schätzungen begnügen. Schätzwerte werden mit einem “Dach” über dem Kennwert gekennzeichnet, s. letzte Spalte in Tabelle 2.1.
In der angewandten Forschung und im praktischen Leben interessieren häufig Fragen wie: “Welche Entscheidung ist (wahrscheinlich) besser?”. Da bekanntlich (fast) keine Aussagen sicher sind, spielt Wahrscheinlichkeit eine wichtige Rolle in den Forschungsfragen bzw. in deren Antworten.
Wahrscheinlichkeit wird oft mit Pr oder p abgekürzt, für engl. probability.
Beispiel 2.4 Sie testen zwei Varianten Ihres Webshops (V1 und V2), die sich im Farbschema unterscheiden und ansonsten identisch sind: Hat das Farbschema einen Einfluss auf den Umsatz?
Dazu vergleichen Sie den mittleren Umsatz pro Tag von V1 vs. V2,
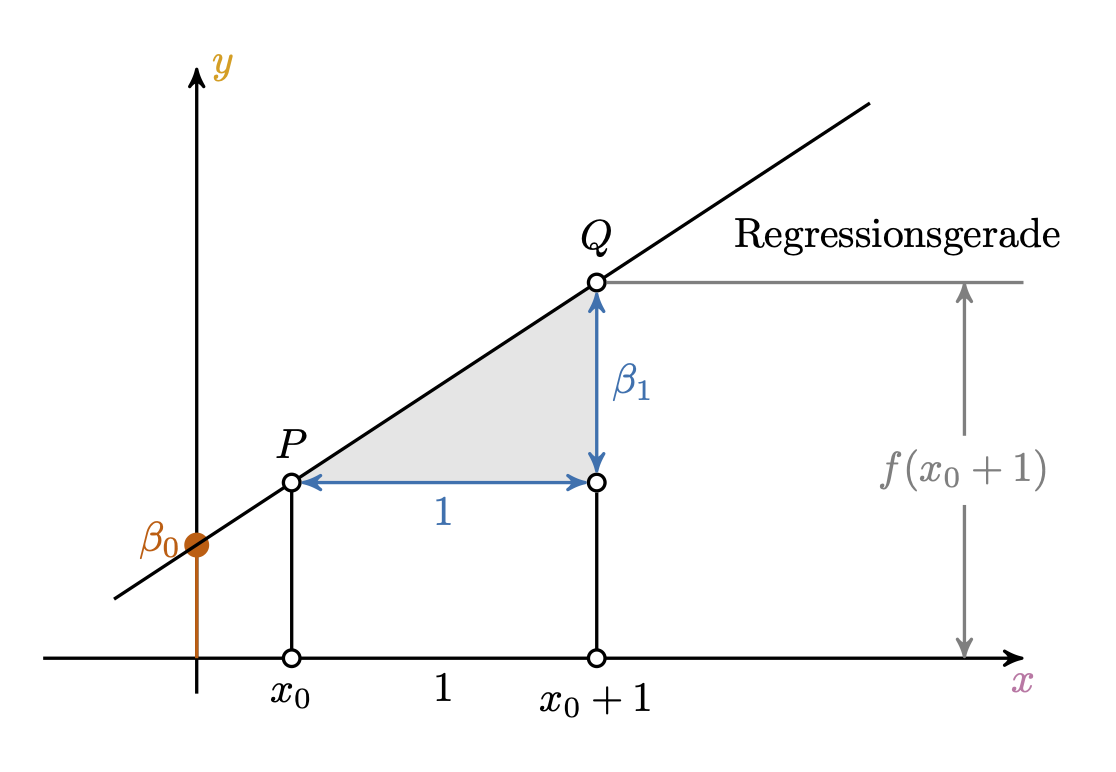
Übungsaufgabe 2.3 (Peer Instruction: Regressionskoeffizienten) Eine Regressionsgerade wird durch zwei Koeffizienten festgelegt: ihren Achsenabschnitt,
- Beschreiben
- Vorhersagen
- Erklären - Kausal
- Erklären - Population
- Alle der oben genannten sind möglich
- Keine der oben genannten
2.3 Modellieren
2.3.1 Modellieren als Grundraster des Erkennens
In In der Wissenschaft – wie auch oft in der Technik, Wirtschaft oder im Alltag – betrachtet man einen Teil der Welt näher, meist mit dem Ziel, eine Entscheidung zu treffen, was man tun wird oder mit dem Ziel, etwas zu lernen. Nun ist die Welt ein weites Feld. Jedes Detail zu berücksichtigen ist nicht möglich. Wir müssen die Sache vereinfachen: Alle Informationen ausblenden, die nicht zwingend nötig sind. Aber gleichzeitig die Strukturelemente der wirklichen Welt, die für unsere Fragestellung zentral sind, beibehalten.
Dieses Tun nennt man Modellieren: Man erstellt sich ein Modell.
Definition 2.3 (Modell) Ein Modell ist ein vereinfachtes Abbild der Wirklichkeit.
Der Nutzen eines Modells ist, einen (übermäßig) komplexen Sachverhalt zu vereinfachen oder überhaupt erst handhabbar zu machen. Man versucht zu vereinfachen, ohne Wesentliches wegzulassen. Der Speck muss weg, sozusagen. Das Wesentliche bleibt. Auf die Statistik bezogen heißt das, dass man einen Datensatz dabei so zusammenfasst, damit man das Wesentliche erkennt.
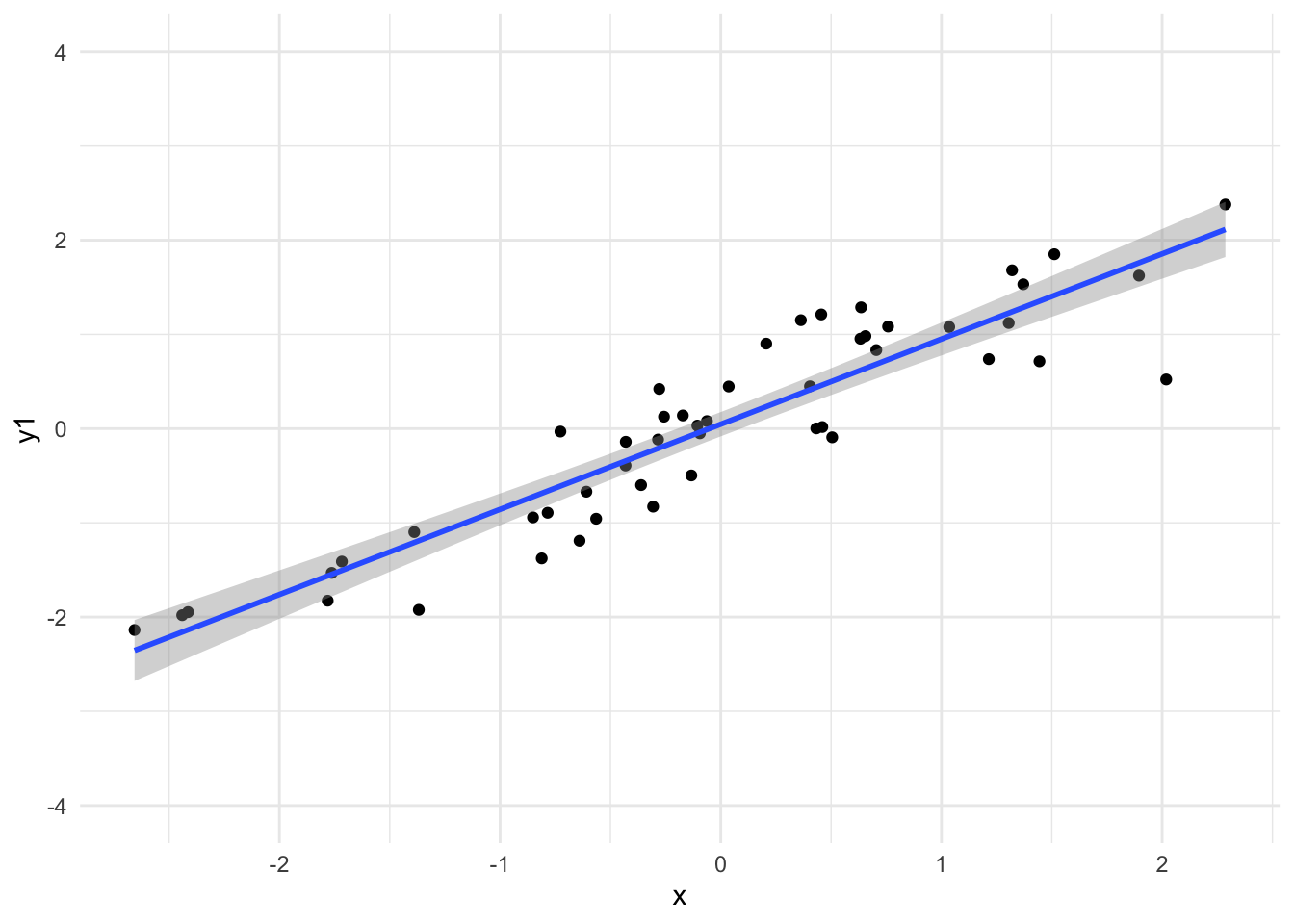
Was ist das “Wesentliche”? Oft interessiert man sich für die Ursachen eines Phänomens. Etwa: “Wie kommt es bloß, dass ich ohne zu lernen die Klausur so gut bestanden habe?”4 Noch allgemeiner ist man dabei häufig am Zusammenhang von X und Y interessiert, s. Abbildung 2.5, die ein Sinnbild von statistischen Modellen widergibt.
Man kann Abbildung 2.5 als ein Sinnbild einer (mathematischen) Funktion lesen.
Definition 2.4 (Funktion) Eine mathematische Funktion
In Mathe-Sprech:
oder:
Die Größe des Zusammenhangs von
Definition 2.5 (Effekt) Der Begriff Effekt im statistisch-wissenschaftlichen Sinn bezeichnet die Größe des statistischen Zusammenhangs (oder der Differenz) zwischen UV und AV in einem Modell, die über den zufälligen Erwartungswert hinausgeht. Effekt ist nicht unbedingt kausal zu verstehen.
Es hört sich zugespitzt an, aber eigentlich ist fast alles, was man tut, Modellieren: Wenn man den Anteil der R-Fans in einer Gruppe Studierender ausrechnet, macht man sich ein Modell: man vereinfacht diesen Ausschnitt der Wirklichkeit anhand einer statistischen Kennzahl, die das forschungsleitende Interesse zusammenfasst. Die Statistik kann man verstehen als ein Verfahren, dass wissenschaftliche Modelle in statistische übersetzt und letztere dann einer empirischen Analyse unterzieht. Alle statistischen Ergebnisse beruhen auf Modelle und sind nur insoweit gültig, wie das zugrundeliegende Modell gültig ist.
2.3.2 Regression zum Modellieren
Einflussreiche Leute schwören auf die Regressionsanalyse (Abbildung 2.6).
Abbildung 2.7 zeigt ein interaktives Beispiel einer linearen Funktion. Sie können Punkte per Klick/Touch hinzufügen.
Alternativ können Sie diese App nutzen, Regressionskoeffizienten, Steigung (slope) und Achsenabschnitt (Intercept), zu optimieren. Dabei meint “optimieren”, die Abweichungen (Residuen, Residualfehler; die roten Balken in der App) zu minimieren.5
Hier finden Sie eine App, die Ihnen gestattet, selber Hand an eine Regressionsgerade zu legen.
Übungsaufgabe 2.4 (VERTIEFUNG Regression mit Animationen erklärt) Lesen Sie diesen Post, der Ihnen mit Hilfe von Bildern und Animationen (okay, und etwas) Text die Grundlagen der Regressionsanalyse erklärt.
Die Regression ist eine Art Schweizer Taschenmesser der Statistik: Für vieles gut einsetzbar. Anstelle von vielen verschiedenen Verfahren des statistischen Modellierens kann man (fast) immer die Regression verwenden. Das ist nicht nur einfacher, sondern auch mathematisch schöner. Wir werden im Folgenden stets die Regression zum Modellieren verwenden. Dann wenden wir die Methoden der Inferenz auf die Kennzahlen der Regression an.
Regression + Inferenz = 💖
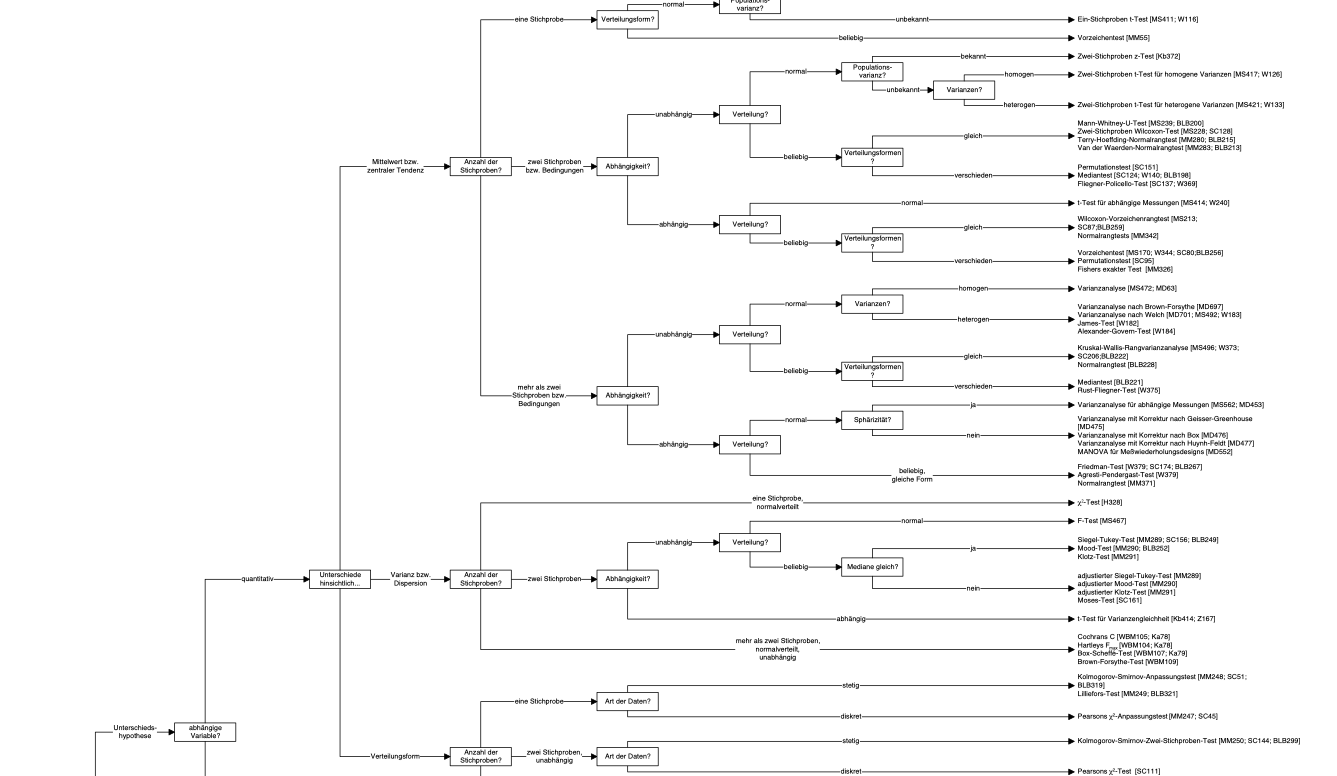
Alternativ zur Regression könnte man sich in den Wald der statistischen Verfahren begeben, wie hier von der Uni Münster als Ausschnitt (!) aufgeführt. Auf dieser Basis kann man meditieren, welches statistischen Verfahren man für eine bestimmte Fragestellung verwenden sollte, s. Abbildung 2.8 (b). Muss man aber nicht – man kann stattdessen die Regression benutzen.
Es ist meist einfacher und nützlicher, die Regression zu verwenden, anstelle der Vielzahl von anderen Verfahren (die zumeist Spezialfälle der Regression sind). In diesem Kurs werden wir für alle Fragestellungen die Regression verwenden.6
Beispiel 2.5 Typische Spezialfälle der Regression sind
- t-Test: UV: zweistufig nominal, AV: metrisch
- ANOVA: UV: mehrstufig nominal, AV: metrisch
- Korrelation: Wenn UV und AV z-standardisiert sind (d.h. Mittelwert von 0 und Standardabweichung von 1 haben), dann ist die Korrelation gleich dem Regressionskoeffizienten
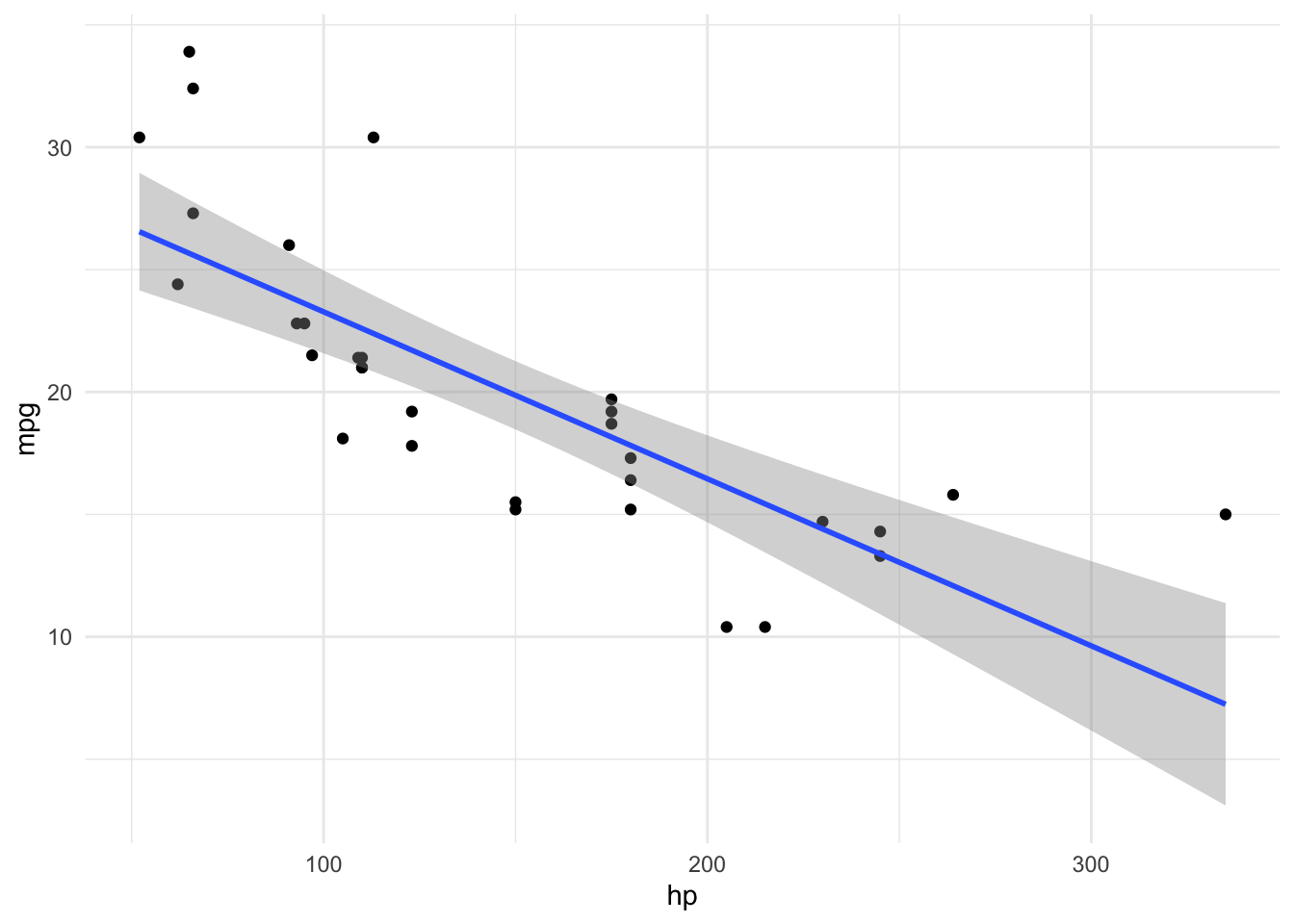
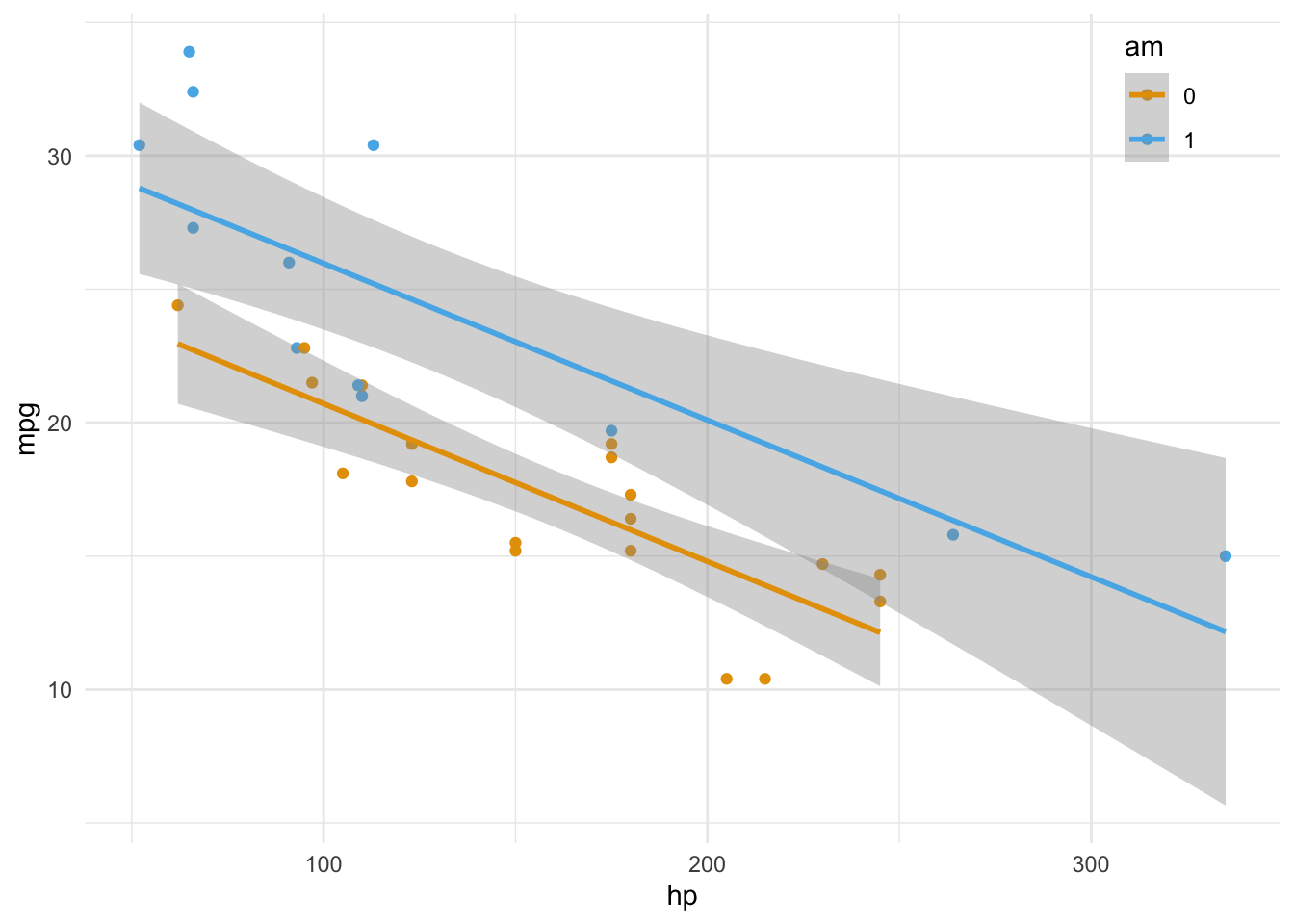
Abbildung 2.9 zeigt die Regressionsgleichung in voller Pracht. Links sieht man eine einfache Regression mit hp als UV (X, auch: Prädiktor) und mpg als AV (Y). Das rechte Teildiagramm zeigt eine multiple Regression mit den UVs hp und am.7 Im einfachsten Fall sind die vom Modell vorhergesagten (geschätzten) Werte,
Theorem 2.1 (Lineares Modell (Regressionsgleichung))
Man nennt alle
Anhand von Theorem 2.1 erkennt man auch, warum man von einem linearen Modell spricht: Y wird als gewichteter Mittelwert mehrerer Summanden berechnet.
Eine Regressionsgerade ist durch zwei Parameter festgelegt: den Achsenabschnitt,
2.4 Populationsinferenz
Definition 2.6 (Populationsinferenz) Populationsinferenz (auch Inferenzstatistik oder schließende Statistik genannt) ist der Teilbereich der Statistik, der sich damit befasst, von den Daten einer begrenzten Stichprobe auf eine zugrundeliegende Grundgesamtheit (Population) zu verallgemeinern (zu schließen).
Deskriptivstatistik (Beschreiben) und Inferenzstatistik (Erklären) gehen Hand in Hand: Mit der Deskriptivstatistik berechnet man Statistiken zur Stichprobe. Dabei resultiert die Stichprobe durch eine zufällige Auswahl von Objekten aus der Grundgesamtheit. Mit der Inferenzstatistik verallgemeinert man von der Stichprobe auf die Grundgesamtheit, s. Abbildung 2.10.
2.4.1 Inferenz beinhaltet Ungewissheit
Inferenzstatistische Schlüsse sind mit Ungewissheit (Unsicherheit über die Zuverlässigkeit der Ergebnisse) behaftet: Schließlich kennt man nur einen Teil (die Stichprobe) eines Ganzen (die Population), möchte aber vom Teil auf das Ganze schließen. Aus diesem begrenzten Wissen resultiert notwendig Ungewissheit über die gesamte Population.
Nichts Genaues weiß man nicht: Schließt man von einem Teil auf das Ganze, so geschieht das unter Unsicherheit. Man spricht von Ungewissheit, da man sich auf die Unsicherheit das Wissen über die Genauigkeit des Schließens bezieht
Schließt man etwa, dass in einer Grundgesamtheit der Anteil der R-Fans bei 42% liegt, so geschieht das unter Unsicherheit; es ist ungewiss. Man ist sich nicht sicher, dass es wirklich 42% in der Population sind – und nicht etwa etwas mehr oder etwas weniger. Schließlich hat man nicht die ganze Population gesehen bzw. vermessen. Sicher ist man sich hingegen für die Stichprobe (Messfehler einmal ausgeblendet). Zur Bemessung der Unsicherheit (Ungewissheit) bedient man sich der Wahrscheinlichkeitsrechnung (wo immer möglich). Die Wahrscheinlichkeitstheorie bzw. -rechnung wird daher auch als die Mathematik des Zufalls bezeichnet.
Definition 2.7 (Zufälliges Ereignis) Unter einem zufälligen (engl. random) Ereignis verstehen wir ein Ereignis, das nicht (komplett) vorherzusehen ist, wie etwa die Augenzahl Ihres nächsten Würfelwurfs. Zufällig bedeutet nicht (zwangsläufig), dass das Ereignisse keine Ursachen besitzt. So gehorchen die Bewegungen eines Würfels den Gesetzen der Physik, nur sind uns diese oder die genauen Randbedingungen nicht (ausreichend) bekannt.
Übungsaufgabe 2.5 🏋 Welche physikalischen Randbedingungen wirken wohl auf einen Münzwurf ein?
Beispiel 2.6 (Beispiele zur Quantifizierung von Ungewissheit) Aussagen mit Unsicherheit können unterschiedlich präzise formuliert sein.
Morgen regnet’s
Methode
Die Maschine fällt demnächst aus
Die Investition lohnt sich
Übungsaufgabe 2.6 🏋 Geben Sie weitere Beispiele an!
2.4.2 Zwei Arten von Ungewissheit
Im Modellieren im Allgemeinen und in Regressionsmodellen im Besonderen lassen sich (mindestens) zwei Arten von Ungewissheiten angeben:
Wie (un)gewiss ist man sich über die Regressionsgewichte?
Wie (un)gewiss ist man sich über die Vorhersagegenauigkeit?
2.4.2.1 Betas: Ungewissheit zur Regressionsgeraden
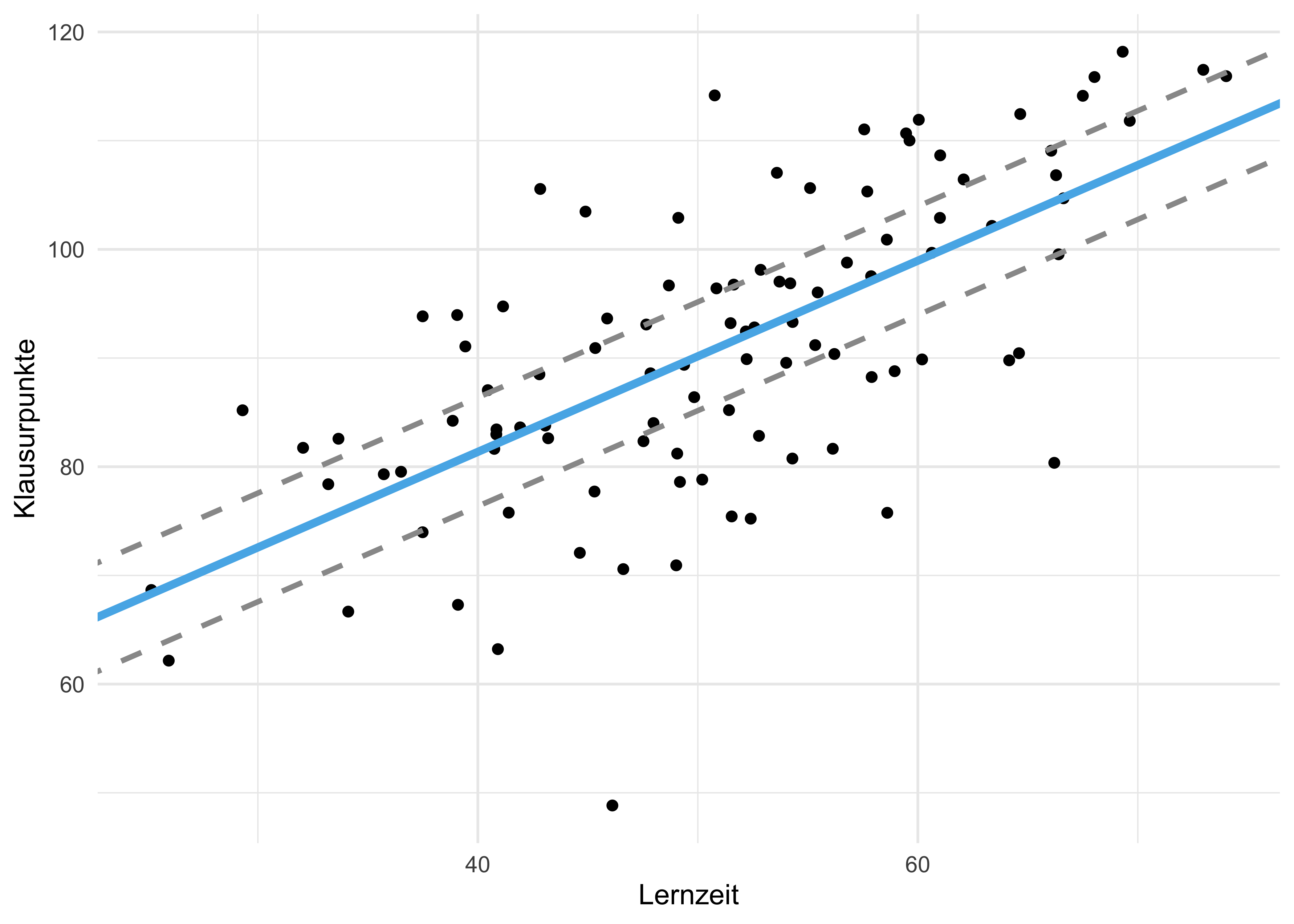
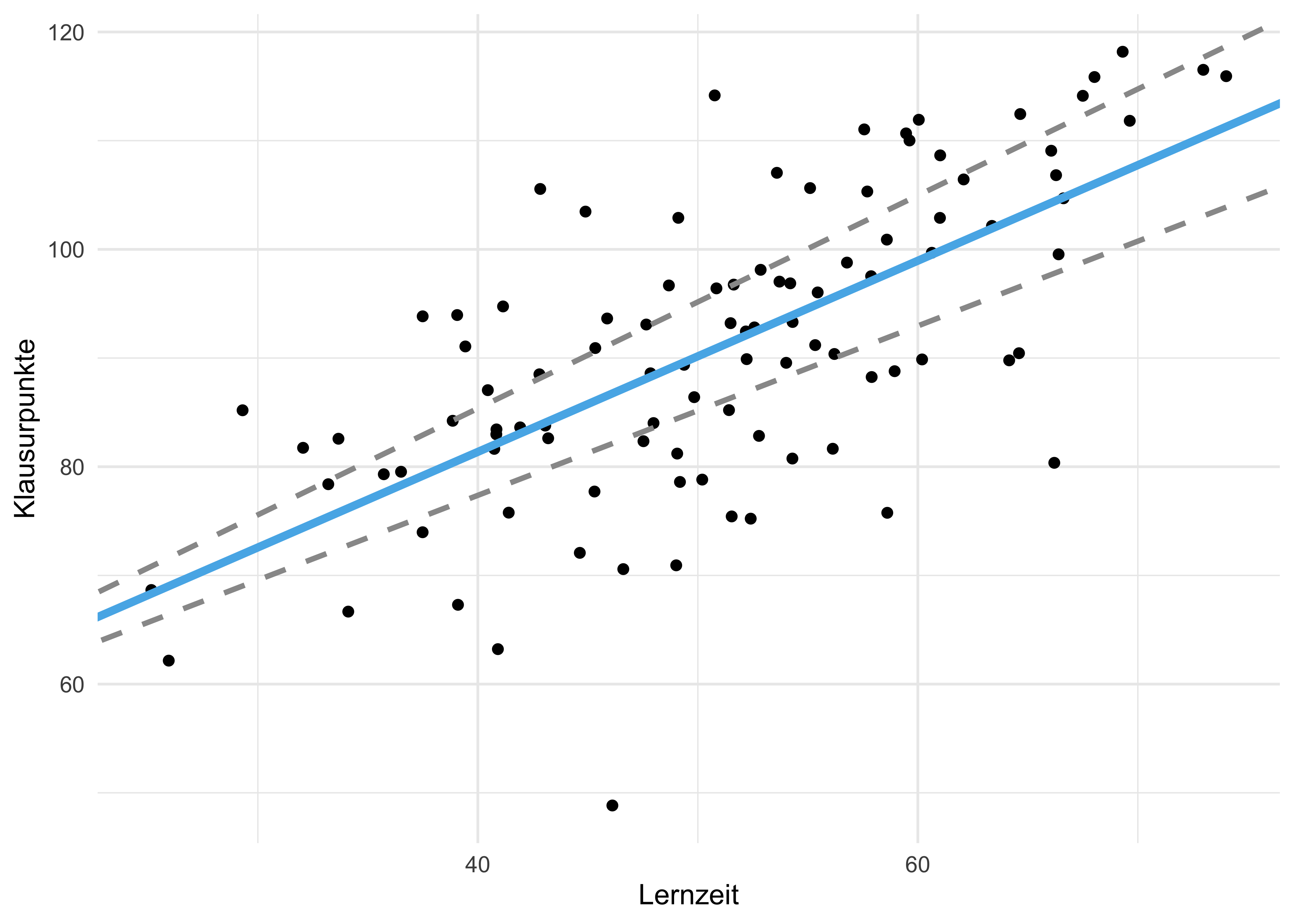
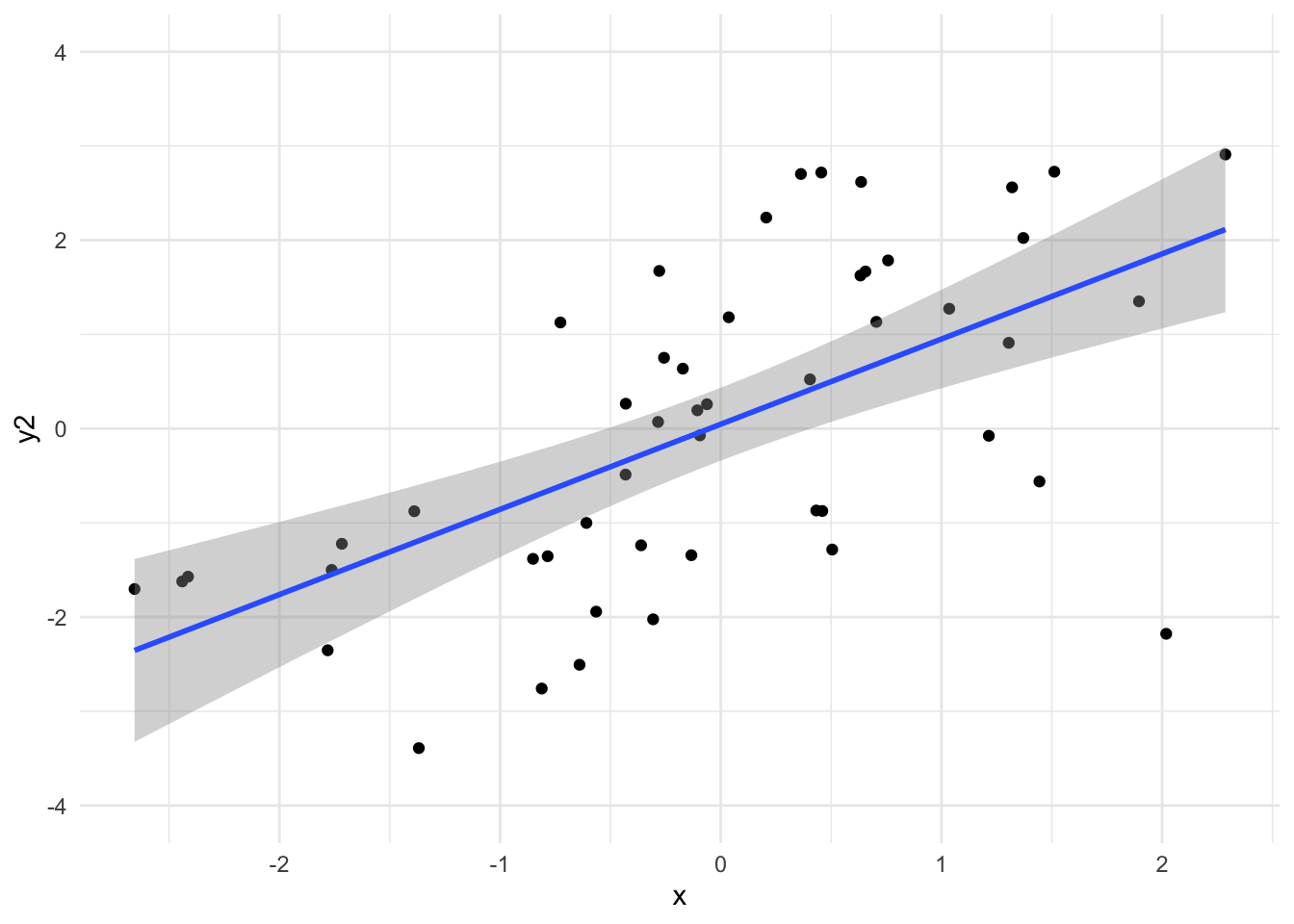
Wenn wir von den Daten der Stichproben auf die Grundgesamtheit schließen, können wir nicht sicher sein, ob die Regressionskoeffizienten (Achsenabschnitt, Steigung der Regressiongeraden) exakt richtig sind, s. Abbildung 2.11.
Wie man in Abbildung 2.12 sieht, können sich die Koeffizienten des Modells (
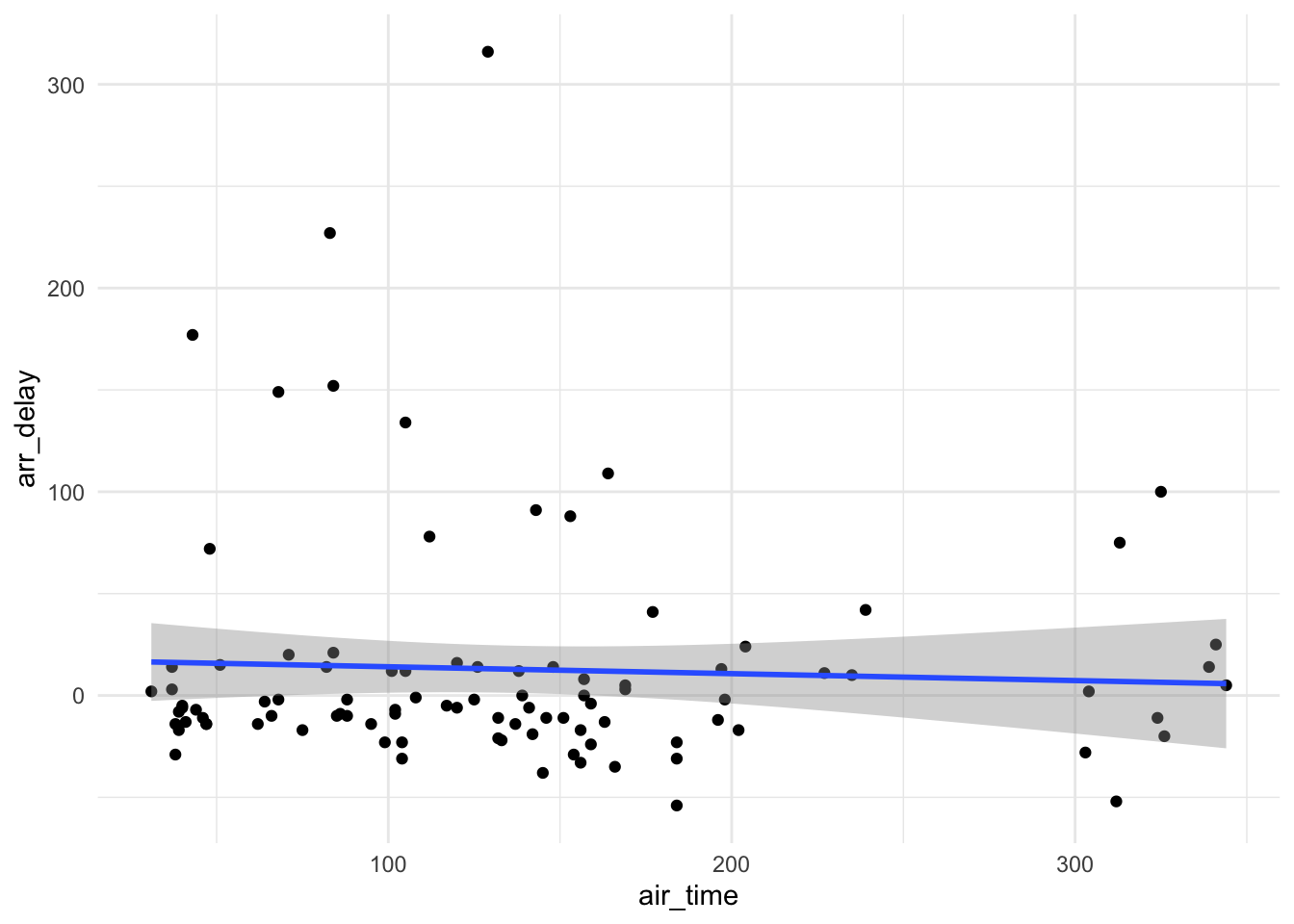
Beispiel 2.7 (Stichproben der New Yorker Flüge) Nehmen wir an, wir ziehen ein paar Zufallstichproben aus der Menge (Population) aller Flüge, die in New York im Jahre 2013 gestartet sind. In jeder Stichprobe berechnen wir eine Regression zwischen Flugzeit und Verspätung des Flugs am Ankunftsort. Sicherlich werden sich die Stichproben in ihren Kennwerten, z.B. in den Koeffizienten der genannten Regression, unterscheiden.
library(nycflights13)
data(flights)
stipro1 <- sample_n(flights, size = 100)
stipro2 <- sample_n(flights, size = 100)
stipro3 <- sample_n(flights, size = 100)Der Grund für die Schwankungen der Modellparameter zwischen den Stichproben ist die Zufälligkeit des Stichprobenziehens. Je nachdem, wie es der Zufall (oder sonst wer) will, landen bestimmte Fälle (Flüge in unserem Beispiel) in unserer Stichprobe. Zumeist unterscheiden sich die Stichproben; theoretisch könnten sie aber auch rein zufällig gleich sein.
Stichproben-Kennwerte schwanken um den tatsächlichen Wert in der Population herum.
Um diese Ungewissheit, die sich in den Schwankungen der Stichproben-Regressionskoeffizienten ausdrückt, anzuzeigen, ist ein “grauer Schleier” um die Regressionsgeraden in Abbildung 2.12 gekennzeichnet. Dieser grauer Schleier gibt also eine Spannbreite anderer, plausibler Lagen der Regressionsgeraden an, die sich in einer anderen Stichprobe auch manifestieren könnten.
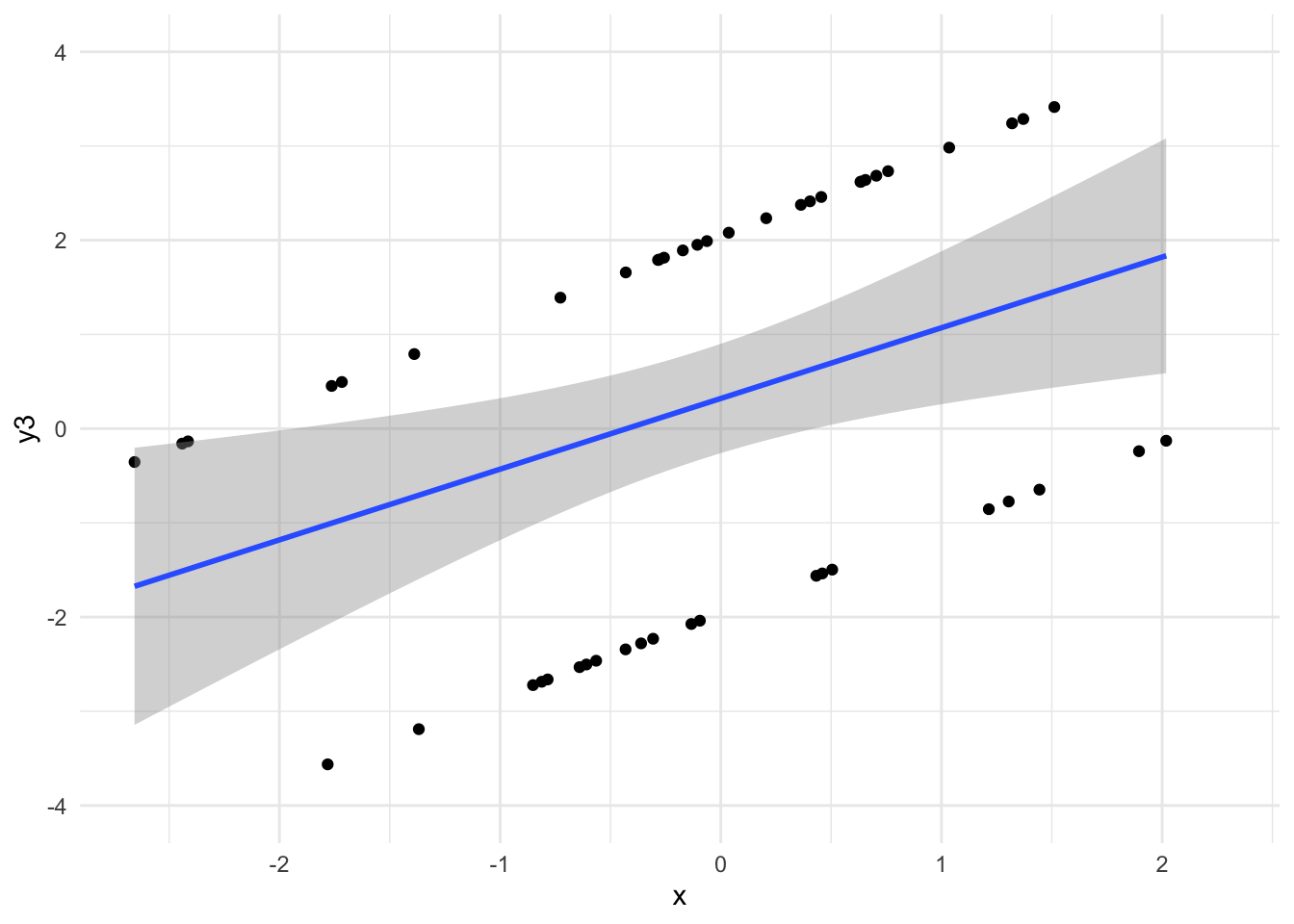
2.4.2.2 Sigma: Ungewissheit zur Genauigkeit der Vorhersage
Angenommen, wir sind uns sicher über die Werte der Modellparameter (
Definition 2.8 (Sigma als mittleren Vorhersagefehler)
2.4.3 Ich weiß, was ich nicht weiß: Ungewissheit angeben
Streng genommen ist eine Inferenz ohne Angabe der Ungewissheit (Genauigkeit der Schätzung) wertlos. Angenommen, jemand sagt, dass sie den Anteil der R-Fans (in der Population) auf 42% schätzt, lässt aber offen wie sicher (präzise) die Schätzung (der Modellparameter) ist. Wir wissen also nicht, ob z.B. 2% oder 82% noch erwartbar sind. Oder ob man im Gegenteil mit hoher Sicherheit sagen kann, die Schätzung schließt sogar 41% oder 43% aus.
Schließt man auf eine Population, schätzt also die Modellparameter, so sollte stets die (Un-)Genauigkeit der Schätzung, also die Ungewissheit des Modells, angegeben sein.
Im Rahmen der Regressionsanalyse schlägt sich die Ungewissheit an zwei Stellen (und in drei Parametern) nieder:
- zur Präzision der Regressionsgeraden
- zur Modellgüte (
2.4.4 Konfidenzintervall
Wir haben gesesehen, dass wir die Werte der Parameter nur mit Ungewissheit angegeben können (s. Abbildung 2.11 und Abbildung 2.13). Um dieser Ungewissheit Rechnung zu tragen, gibt man nicht nur einen einzelnen Wert an, einen Punktschätzer, sondern man gibt ein Schätzbereich an auf Basis der Daten, s. Tabelle 2.2.
Man spricht anstatt von Schätzbereich auch von einem Konfidenzintervall.9
model_parameters(lm_toni) |>
print_md()Unser Modell gibt den 95%-Schätzbereich für den Achsenabschnitt an ca. von 36 bis 56 Klausurpunkte Die Steigung wird geschätzt auf ca. 0.7 bis 1.1 Klausurpunkte pro Stunde Lernzeit.
Definition 2.9 (Konfidenzintervall) Ein Konfidenzintervall (confidence intervall, CI) ist ein Oberbegriff für Schätzbereiche für Parameter wie Regressionskoeffizienten. Die Grenzen eines Konfidenzintervall markieren die Grenzen eines Bereichs plausibler Werte für einen Parameter.
Es gibt verschiedene Arten, Konfidenzintervalle zu berechnen; wir sprechen in späteren Kapiteln dazu ausführlicher. Ein Konfidenzintervall wird häufig mit 90% oder 95% Genauigkeit angegeben. Im Kontext der Bayes-Analyse - auf der dieser Kurs aufbaut - ist ein Konfidenzintervall einfach zu interpretieren. Sagen wir, wir finden, dass in einem Modell ein 95%-Konfidenzintervall für den Anteil der R-Fans angegeben wird, dass sich von 40 bis 44 Prozent erstreckt. Dieser Befund lässt sich so interpretieren:
“Laut Modell liegt der gesuchte Anteil der R-Fans mit einer Wahrscheinlichkeit von 95% im Bereich von 40 bis 44 Prozentpunkten.”
Übungsaufgabe 2.7 Geben Sie Beispiele für Konfidenzintervalle an.
2.5 Frequentistische Inferenz vs. Bayes-Inferenz
Es gibt zwei Hauptarten von Inferenzstatistik: Frequentistische Inferenz und Bayes-Inferenz.
Frequentismus: Klassische Inferenz
- Ziel ist es, den Anteil von Fehlentscheidungen auf lange Sicht zu kontrollieren.
- Keine Berücksichtigung von Vorwissen zum Sachgegenstand
- Wahrscheinlichkeit wird über relative Häufigkeiten definiert.
- Es ist nicht möglich, die Wahrscheinlichkeit einer Hypothese bzw. eines Werts in der Population (eines Parameters) anzugeben.
- Stattdessen wird angegeben, wie häufig eine vergleichbare Datenlage zu erwarten ist, wenn der Versuch sehr häufig (unendlich oft) wiederholt ist.
- Ein Großteil der Forschung (in den Sozialwissenschaften) verwendet (aktuell) diesen Ansatz.
Bayesianische Inferenz
- Ziel ist es, die Wahrscheinlichkeit einer Hypothese korrekt zu bemessen.
- Vorwissen (Priori-Wissen) fließt explizit in die Analyse ein (zusammen mit den Daten).
- Wenn das Vorwissen gut ist, wird die Vorhersage durch das Vorwissen genauer, ansonsten ungenauer.
- Die Wahl des Vorwissens muss explizit (kritisierbar) sein.
- In der Bayes-Inferenz sind Wahrscheinlichkeitsaussagen für Hypothesen möglich.
- Die Bayes-Inferenz erfordert mitunter viel Rechenzeit und ist daher erst in den letzten Jahren (für gängige Computer) komfortabel geworden.
2.5.1 Frequentistische Inferenz und der p-Wert
Der zentrale Kennwert der Frequentistische Inferenz (synonym: Frequentismus) ist der p-Wert.
Der p-Wert ist so definiert, vgl. Wasserstein & Lazar (2016):
Wie hoch ist die Wahrscheinlichkeit eines empirischen Befunds (oder noch extremere Werte), vorausgesetzt die Nullhypothese
gilt und man wiederholt den Versuch unendlich oft (mit gleichen Bedingungen, aber zufällig verschieden und auf Basis unseres Modells)?
Einfacher gesagt:
Der p-Wert ist die Wahrscheinlichkeit, ein Ergebnis zu erhalten, das mindestens so extrem ist wie das beobachtete, unter der Annahme, dass es keinen Effekt gibt.
Noch einfacher:
Man nimmt an, dass es keinen Effekt gibt (z.B. kein Zusammenhang zwischen den untersuchten Variablen)
Dann fragt man: Wie überraschend wären meine Daten unter dieser Annahme?
Der p-Wert gibt genau diese Überraschungs-Wahrscheinlichkeit an.
Übungsaufgabe 2.8 🏋 Recherchieren Sie eine Definition des p-Werts und lesen Sie sie einem Freund. Beobachten sie die Reaktionen auf Ihre Erklärung.
Der p-Wert wird oft falsch verstanden (Badenes-Ribera et al., 2016). Aber er ist auch nicht leicht zu verstehen, meint Meister Yoda, s. Abbildung 2.14. Hier sind einige FALSCHE Interpretationen zum p-Wert laut der Autoren:
- 🙅♀ Der p-Wert würde die Wahrscheinlichkeit der Nullhypothese oder der Forschungshypothese angeben. 🙊 FALSCH!
- 🙅♀ Der p-Wert würde ein inhaltlich bedeutsames, praktisch signifikantes Ergebnis anzeigen. 🙊 FALSCH!
Ein frequentistisches Konfidenzintervall macht keine Aussage zur Wahrscheinlichkeit eines Werts in der Population (eines Parameters). Stattdessen wird eine Aussage über das Ergebnis einer sehr häufig wiederholten Stichprobenziehung berichtet. Ob ein bestimmtes (unseres, Ihres) den wahren Wert enthält, bzw. mit welcher Wahrscheinlichkeit es den wahren Wert enthält, darüber macht das frequentistische Konfidenzintervall keine Aussagen.
2.5.2 Bayes-Inferenz
Die zentrale Statistik der Bayes-Inferenz bzw. (synonym) Bayes-Statistik ist die Posteriori-Verteilung.
Die Posteriori-Verteilung beantwortet uns die Frage: “Wie wahrscheinlich ist die Forschungshypothese (oder Varianten von ihr), jetzt, nachdem wir die Daten kennen, auf Basis unseres Modells?”
In der Bayes-Statistik sind Aussagen folgender Art erlaubt:
Mit einer Wahrscheinlichkeit von 95% ist der neue Webshop besser als der alte. Mit einer Wahrscheinlichkeit von 89% liegt die Wirksamkeit des neuen Medikaments zwischen 0.1 und 0.4.
2.5.3 Statistische Signifikanz
Im Frequentismus spricht man von statistischer Signifikanz, wenn der p-Wert kleiner ist als 5%:
In der Bayes-Statistik ist der Begriff der Signifikanz nicht einheitlich definiert. Mit Bezug auf Gelman et al. (2021) (S. 57) wird in diesem Buch der Begriff wie folgt definiert - mit Gültigkeit sowohl für Bayes-Statistik als auch für Frequentistische Statistik.
Definition 2.10 (Statistische Signifikanz) Ist der Wert Null nicht im Schätzbereich enthalten, so liegt ein statistisch signifikantes Ergebnis vor.
Oft werden 95%-Konfidenzintervalle verwendet, obwohl das nur eine Konvention ist. Die Signifikanzaussage bezieht sich immer auf ein Schätzbereich bestimmter Größe, z.B. 95% (und des Modells inklusive Daten).
Liegt ein statistisch signifikantes Ergebnis vor, so verwirft man die Nullhypothese und akzeptiert die Alternativhypothese (synonym: Effekthypothese).
Definition 2.11 (Exakte Nullhypothese) Die exakte Nullhypothese (meist kurz nur als Nullhypothese bezeichnet),
Definition 2.12 (Alternativhypothese (Effekthypothese)) Eine Hypothese, die besagt, dass es einen (substanziellen) Effekt gibt. Das kann z.B. ein Unterschied zwischen den untersuchten Gruppen sein oder ein Zusammenhang zwischen den untersuchten Variablen. Logisch betrachtet ist die Alternativhypothese meist das Gegenteil der Nullhypothese.
Beispiel 2.8 (Beispiele für Effekthypothesen)
- Die Trefferquote der Münze ist
- Der Unterschied im mittleren Gewicht zwischen den Gruppen beträgt ca. 500-600 g.
- Der Korrelationskoeffizient
- Der standardisierte Regressionskoeffizient
- Der Unterschied in Gestimmtheit vor vs. nach der Induktion von Einsamkeit liegt bei
Beispiel 2.9 (Beispiele für Nullhypothesen)
- H₀: μ = 100 (Der Populationsmittelwert beträgt 100)
- H₀: μ₁ = μ₂ (Es gibt keinen Unterschied zwischen den Mittelwerten zweier Gruppen)
- H₀: ρ = 0 (Es besteht kein linearer Zusammenhang zwischen zwei Variablen)
- H₀: π = 0.5 (Die Wahrscheinlichkeit für “Erfolg” beträgt 50%; die Münze ist “fair”)
- H₀: μ₁ = μ₂ = μ₃ = μ₄ (Alle Gruppenmittelwerte sind gleich; bei ANOVA)
- H₀: β₁ = 0 (Der Regressionskoeffizient ist null; kein Effekt des Prädiktors)
- H₀: σ₁² = σ₂² (Die Varianzen zweier Populationen sind gleich)
Statistische Signifikanz im Frequentismus (nicht in der Bayes-Statistik) ist auch eine Funktion der Stichprobengröße: Wenn die Stichprobe groß genug ist, wird jeder Test signifikant. Daher hat ein signifikantes Ergebnis zwei mögliche Ursachen: Der Effekt ist groß oder (auch) die Stichprobe ist groß, s. Abbildung 2.15.
Übrigens sollte man nicht nur von “Signifikanz”, sondern von “statistischer Signifikanz” sprechen, um klar zu machen, dass man nicht ein Alltagsverständnis von Signifikanz (“groß”, “bedeutsam”) meint, sondern einen wohl definierten statistischen Begriff. Das ist wichtig, weil es sonst leicht zu Fehlinterpretationen kommt.
Makowski et al. (2019) schlagen vor, welche Kennwerte der Bayes-Statistik analog zum
Übungsaufgabe 2.9 (Abhängigkeit vom Handy) Die Studie von Kabadayi (2024) untersucht den Zusammenhang von Smartphone-Abhängigkeit mit gesundheitlichen Problemen wie Depression, Stress, Einsamkeit und Schlafschwierigkeiten bei Heranwachsenden.
Lesen Sie den Abstract der Studie und Tabelle 2 (sowie alle Teile, die Sie benötigen, um Tabelle 2 zu verstehen).
- Was ist der stärkste Zusammenhang bzgl. Smartphone-Abhängigkeit? Wie hoch ist er? Wie groß ist die erklärte Varianz des Zusammenhangs?
- Zwischen welchen Variablen findet sich ein “statistisch signifikanter” Zusammenhang?
- Erklären Sie, was ein “statistisch signifikanter Zusammenhang” hier bedeutet?
2.5.4 Frequentist und Bayesianer
Im Cartoon 1132 von xkcd wird sich über das Nicht-Berücksichtigen von Vorab-Informationen (Prior-Verteilung) lustig gemacht, s. Abbildung 2.16.
Übungsaufgabe 2.10 (Peer Instruction: p-Wert) Der p-Wert ist der zentrale Kennwert der frequentistischen Statistik. Aber er wird immer wieder missverstanden. Welche Aussage zum p-Wert ist korrekt?
- Ein p-Wert von 0,04 bedeutet, dass die Nullhypothese mit 96 % Wahrscheinlichkeit falsch ist.
- Ein p-Wert größer als 0,05 beweist, dass die Nullhypothese wahr ist.
- Ein kleiner p-Wert bedeutet, dass ein großer Effekt vorliegt.
- Ein p-Wert von 0,01 bedeutet, dass sich bei Wiederholung der Studis mit 99% wieder ein signifikantes Ergebnis finden wird.
- Keine der oben genannten.
2.6 Vertiefung
2.6.1 Vertiefung – Frequentistische Konfidenzintervalle werden oft falsch verstanden (Vertiefung10)
Frequentistische Konfidenzintervalle werden oft falsch verstanden, wie die folgende Studie zeigt. Das liegt aber nicht daran, dass die Menschen zu dumm sind, sondern dass frequentistische Konfidenzintervalle für viele Menschen kontraintuitiv sind.
Hoekstra et al. (2014) berichten von einer Studie, in der
Den Versuchpersonen wurde folgender Fragebogen vorgelegt, s. Abbildung 2.17.
Kurz gesagt war die Frage, die die Befragten beantworten sollten:
In einem Experiment wird ein 95%-Konfidenzintervall mit dem Bereich von 0.1 bis 0.4 beichtet. Welcher der folgenden sechs Aussagen sind richtig bzw. falsch?
Mit “Konfidenzintervall” meinen die Forschenden ein frequentistisches Konfidenzintervall.
Alle diese sechs Aussagen sind FALSCH. Die Aussagen lauten:
Die Wahrscheinlichkeit, dass der wahre Mittelwert größer als 0 ist, beträgt mindestens 95 %.
Die Wahrscheinlichkeit, dass der wahre Mittelwert gleich 0 ist, ist kleiner als 5 %.
Die „Nullhypothese“, dass der wahre Mittelwert gleich 0 ist, ist wahrscheinlich falsch.
Es gibt eine 95%ige Wahrscheinlichkeit, dass der wahre Mittelwert zwischen 0,1 und 0,4 liegt.
Wir können mit 95%iger Sicherheit sagen, dass der wahre Mittelwert zwischen 0,1 und 0,4 liegt.
Wenn wir das Experiment immer wieder wiederholen würden, dann liegt der wahre Mittelwert in 95 % der Fälle zwischen 0,1 und 0,4.
Aussagen 1-4 weisen den Hypothesen bzw. den Parametern eine Wahrscheinlichkeit zu, was im Frequentismus nicht erlaubt ist. Aussagen 5-6 spezifizieren die Grenzen des Schätzintervalls, allerdings kann das Konfidenzintervall nur Aussagen zu den zugrundeliegenden Stichproben, nicht zum Schätzintervall, machen.
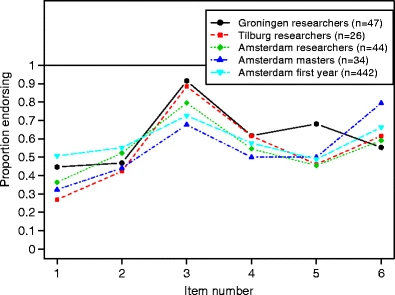
Die Ergebnisse zeigen, dass die Aussagen mehrheitlich falsch verstanden wurden, also mit “stimmt” angekreuzt wurden, s. Abbildung 2.18.
2.6.2 Zielart Erklären – Kausalinferenz
Mittels Kausalinferenz können wir schließen, welche Variablen Ursachen und welche Wirkung sind – und welche Variablen Scheinkorrelation erzeugen. Das ist wichtig, denn nur wenn man die Ursache kennt, weiß man, was man tun muss, um eine Wirkung zu erzielen.
2.6.2.1 Studie A: Östrogen
Medikament einnehmen? Oder lieber nicht? Mit Blick auf Tabelle 12.1: Was raten Sie dem Arzt? Medikament einnehmen, ja oder nein?
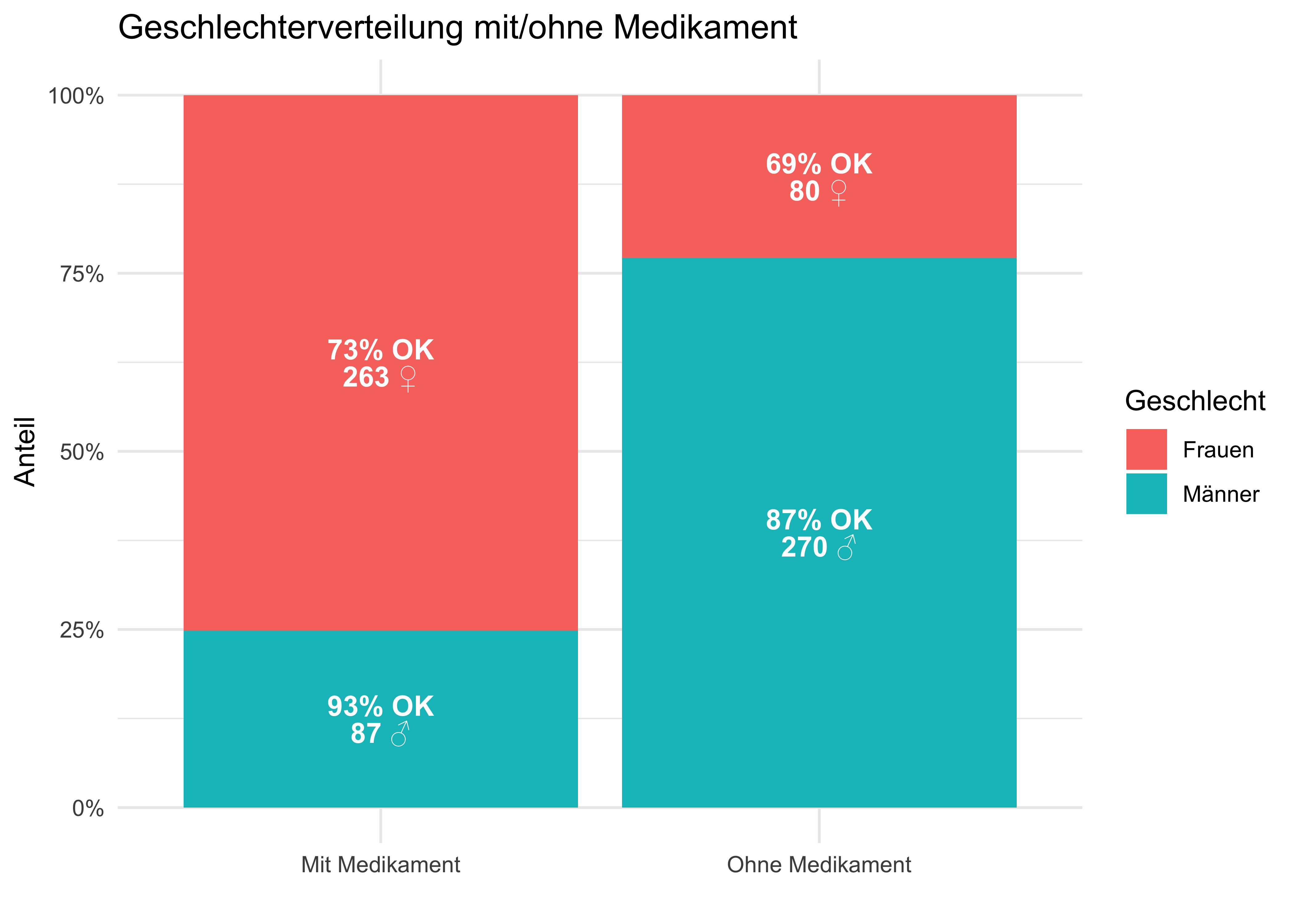
Abbildung 2.19 zeigt die Daten aus Tabelle 12.1 in einem Balkendiagram.
Die Daten stammen aus einer (fiktiven) klinischen Studie,
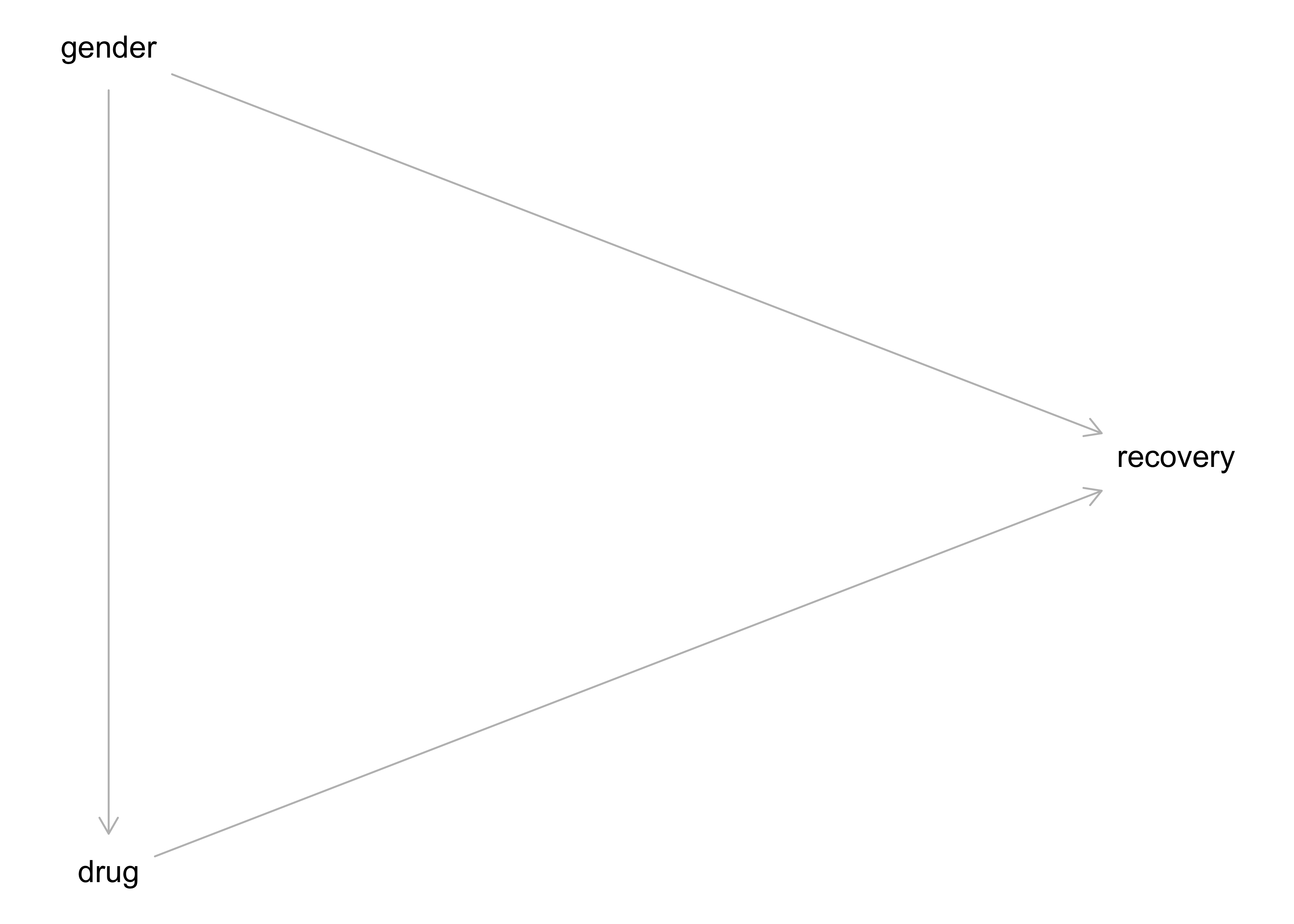
In Wahrheit sehe die kausale Struktur so aus: Das Geschlecht (Östrogen) hat einen positiven (+) Einfluss auf Einnahme des Medikaments und negativen Einfluss (-) auf Heilung. Das Medikament hat einen positiven (+) Einfluss auf Heilung. Betrachtet man die Gesamt-Daten zur Heilung, so ist der Effekt von Geschlecht (Östrogen) und Medikament vermengt (konfundiert, confounded). Die kausale Struktur, also welche Variable beeinflusst bzw. nicht, ist in Abbildung 12.1 dargestellt.
Betrachtung der Gesamtdaten zeigt in diesem Fall einen konfundierten Effekt: Geschlecht konfundiert den Zusammenhang von Medikament und Heilung.
Aufteilen in Teilgruppen (Männer bzw. Frauen) ist also in diesem Fall der korrekte, richtige Weg. Achtung: Das Stratifizieren ist nicht immer und nicht automatisch die richtige Lösung. Stratifizieren bedeutet, den Gesamtdatensatz in Gruppen oder “Schichten” (“Strata”). Würde man die Gesamzahl an Patienten mit vs. ohne Medikatment vergleichen, käme man zu einem falschen Schluss.
2.6.2.2 Studie B: Blutdruck
Medikament einnehmen? Oder lieber nicht?
Mit Blick auf Tabelle 12.2: Was raten Sie dem Arzt? Medikament einnehmen, ja oder nein?
Die Daten stammen aus einer (fiktiven) klinischen Studie,
Kausalmodell zur Studie B
Das Medikament hat einen (absenkenden) Einfluss auf den Blutdruck. Gleichzeitig hat das Medikament einen (toxischen) Effekt auf die Heilung. Verringerter Blutdruck hat einen positiven Einfluss auf die Heilung. Sucht man innerhalb der Leute mit gesenktem Blutdruck nach Effekten, findet man nur den toxischen Effekt: Gegeben diesen Blutdruck ist das Medikament schädlich aufgrund des toxischen Effekts. Der positive Effekt der Blutdruck-Senkung ist auf diese Art nicht zu sehen.
Das Kausalmodell von Studie B ist in Abbildung 12.2 dargestellt.
Betrachtung der Teildaten zeigt nur den toxischen Effekt des Medikaments, nicht den nützlichen (Reduktion des Blutdrucks).
Betrachtung der Gesamtdaten zeigt in diesem Fall den wahren, kausalen Effekt. Stratifizieren wäre falsch, da dann nur der toxische Effekt, aber nicht der heilsame Effekt sichtbar wäre.
2.6.2.3 Studie A und B: Gleiche Daten, unterschiedliches Kausalmodell
Vergleichen Sie die DAGs Abbildung 12.1 und Abbildung 12.2, die die Kausalmodelle der Studien A und B darstellen: Sie sind unterschiedlich. Aber: Die Daten sind identisch.
Kausale Interpretation - und damit Entscheidungen für Handlungen - war nur möglich, da das Kausalmodell bekannt ist. Die Daten alleine reichen nicht (bei Beobachtungsstudien).
2.6.2.4 Sorry, Statistik: Du allein schaffst es nicht
Datenanalyse alleine reicht nicht für Kausalschlüsse. 🧟
Kausalinferenz 📚 plus Datenanalyse 📊 erlaubt Kausalschlüsse. 📚➕📊 🟰 🤩
Für Entscheidungen (“Was soll ich tun?”) braucht man kausales Wissen. Kausales Wissen basiert auf einer Theorie (Kausalmodell) plus Daten.
2.7 Fazit
Kontinuierliches Lernen ist der Schlüssel zum Erfolg.
Wenn Sie an einer (nicht prüfungsrelevanten) Vertiefung interessiert sind, lesen Sie die Einführung zum Thema Modellieren bei Poldrack (2022) (Kap. 5.1).
2.8 Aufgaben
Schauen Sie sich die Aufgaben mit dem Tag inference auf dem Datenwerk an.
2.8.1 Paper-Pencil-Aufgaben
2.8.2 Aufgaben, für die man einen Computer braucht
2.9 —
Ziele existieren nicht “in echt” in der Welt. Wir denken sie uns aus. Ziele haben also keine ontologische Wirklichkeit, sie sind epistemologische Dinge (existieren nur in unserem Kopf). Das heißt, dass man sich nach Belieben Ziele ausdenken kann. Allerdings hilft es, wenn man andere Menschen vom Nutzen der eigenen Ideen überzeugen kann.↩︎
MeistensManchmal darf man bei der Statistik nicht nach einem tieferen Sinn suchen. Ist Statistik eine Art moderne Kunst?↩︎Manch einer hätte mit mehr gerechnet; andere mit weniger…↩︎
Das ist natürlich nur ein fiktives, komplett unrealistisches Beispiel, das auch unklaren Ursachen den Weg auf diese Seite gefunden hat.↩︎
Wie Jonas Kristoffer Lindeløv uns erklärt, sind viele statistische Verfahren, wie der sog. t-Test Spezialfälle der Regression.↩︎
Der Datensatz
mtcarswird gerne als Studienobjekt verwendet, da er einfach ist und für viele Beispiele geeignet. Wenn Sie sich einen Sachverhalt an einem einfachen Datensatz vergegenwärtigen wollen, bietet sich auch der Datensatzmtcarsan. Zudem ist er “fest in R eingebaut”; mitdata(mtcars)können Sie ihn verfügbar machen.↩︎Tatsächlich gibt es mehrere Synonyme oder ähnliche Begriffe für Konfidenzintervall. Wir kommen später darauf detaillierter zu sprechen.↩︎
nicht prüfungsrelevant↩︎