9  Einfache lineare Modelle

9.1 Lernsteuerung

9.1.1 Position im Modulverlauf

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

9.1.2 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können …

• Das Zusammenspiel von Apriori-Verteilungen und linearem Modell zur Berechnung der Likelihood erläutern
• die Post-Verteilung für einfache lineare Modelle in R berechnen
• zentrale Informationen zu Modellparametern des Regressionsmodells – wie Lage– oder Streuungsmaße und auch Schätzintervalle - aus der Post-Verteilung herauslesen

9.1.3 Begleitliteratur

Der Stoff dieses Kapitels orientiert sich an McElreath (2020), Kap. 4.4.

9.1.4 Vorbereitung im Eigenstudium

• Statistik1, Kap. “Geradenmodelle 1”
• Statistik1, Abschnitt “z-Transformation”

9.1.5 Benötigte R-Pakete

In diesem Kapitel benötigen Sie folgende R-Pakete.

library(tidyverse)
library(easystats)
library(rstanarm)  # Bayes-Golem
library(ggpubr)  # Datenvisualisierung

Da wir in diesem Kapitel immer mal wieder eine Funktion aus dem R-Paket {easystats} verwenden: Hier finden Sie eine Übersicht aller Funktionen des Pakets.¹

9.1.6 Benötigte Daten

In diesem Kapitel benötigen wir den Datensatz zu den !Kung-Leuten, aus der Datei Howell1a.csv, McElreath (2020).

Kung_path <- "https://raw.githubusercontent.com/sebastiansauer/Lehre/main/data/Howell1a.csv"

kung <- read.csv(Kung_path)

kung_erwachsen <- kung %>% filter(age > 18)

1

Pfad zum Datensatz; Sie müssen online sein, um die Daten herunterzuladen.

2

Daten einlesen

3

Auf Erwachsene Personen begrenzen (d.h. Alter > 18)

9.1.7 Einstieg

Übungsaufgabe 9.1 (Grundkonzepte der linearen Regression) Fassen Sie die Grundkonzepte der linearen Regression kurz zusammen! $◻$

Übungsaufgabe 9.2 (Was ist eine Post-Verteilung und wozu ist sie gut?) Erklären Sie kurz, was eine Post-Verteilung ist – insbesondere im Zusammenhang mit den Koeffizienten einer einfachen Regression – und wozu sie gut ist. $◻$

9.1.8 Überblick

Dieses Kapitel stellt ein einfaches Regressionsmodell vor, wo die Körpergröße auf das Gewicht zurückgeführt wird; also ein sehr eingängiges Modell.
Neu (im Vergleich zu einer Frequentistischen Regression mit lm) ist dabei lediglich, dass die drei Parameter des Modells – ${\beta }_0$, ${\beta }_1$, $\sigma$ – jetzt über eine Post-Verteilung verfügen. Die Post-Verteilung ist der Zusatznutzen der Bayes-Statistik. Die “normale” Regression hat uns nur einzelne Werte für die Modellparameter geliefert (“Punktschätzer”). Mit Bayes haben wir eine ganze Verteilung pro Parameter; das ist informationsreicher als mit der Frequentistischen Regressionsanalyse.

9.2 Den Datensatz verstehen

9.2.1 Statistiken zum !Kung-Datensatz

Tabelle 9.1 zeigt die zentralen deskriptiven Statistiken zum !Kung-Datensatz.

Kung_path <- "data/Howell1a.csv"  
kung <- read_csv(Kung_path)  

kung_erwachsen <- kung %>% filter(age > 18)

describe_distribution(kung_erwachsen)

Tabelle 9.1: Verteiung der (metrischen) Variablen im !Kung-Datensatz

Variable	Mean	SD	IQR	Range	Skewness	Kurtosis	n	n_Missing
height	154.64	7.77	12.06	(136.53, 179.07)	0.14	-0.50	346	0
weight	45.05	6.46	9.14	(31.52, 62.99)	0.14	-0.53	346	0
age	41.54	15.81	22.00	(19.00, 88.00)	0.68	-0.20	346	0
male	0.47	0.50	1.00	(0.00, 1.00)	0.10	-2.00	346	0

Wie aus Tabelle 9.1 abzulesen ist, beträgt das mittlere Körpergewicht (weight) liegt ca. 45kg (sd ca 7 kg).

Wir brauchen explorative Datenanalyse (EDA) nicht wirklich, um einfache Bayes-Regressionen zu verstehen. Aber EDA hilft, die Daten zu verstehen, was essenziell ist, wenn man Erkenntnisse aus den Daten gewinnen will. Das Paket DataExplorer hat ein paar nette Hilfen zur explorativen Datenanalyse.

library(DataExplorer)

Was man im Rahmen einer EDA stets prüfen sollte, sind fehlende Werte. Gibt es in diesem Datensatz fehlende Werte? Nein, s. Abb. Abbildung 9.1.

kung_erwachsen %>% plot_missing()

Abbildung 9.1: Fehlende Werte - fehlen.

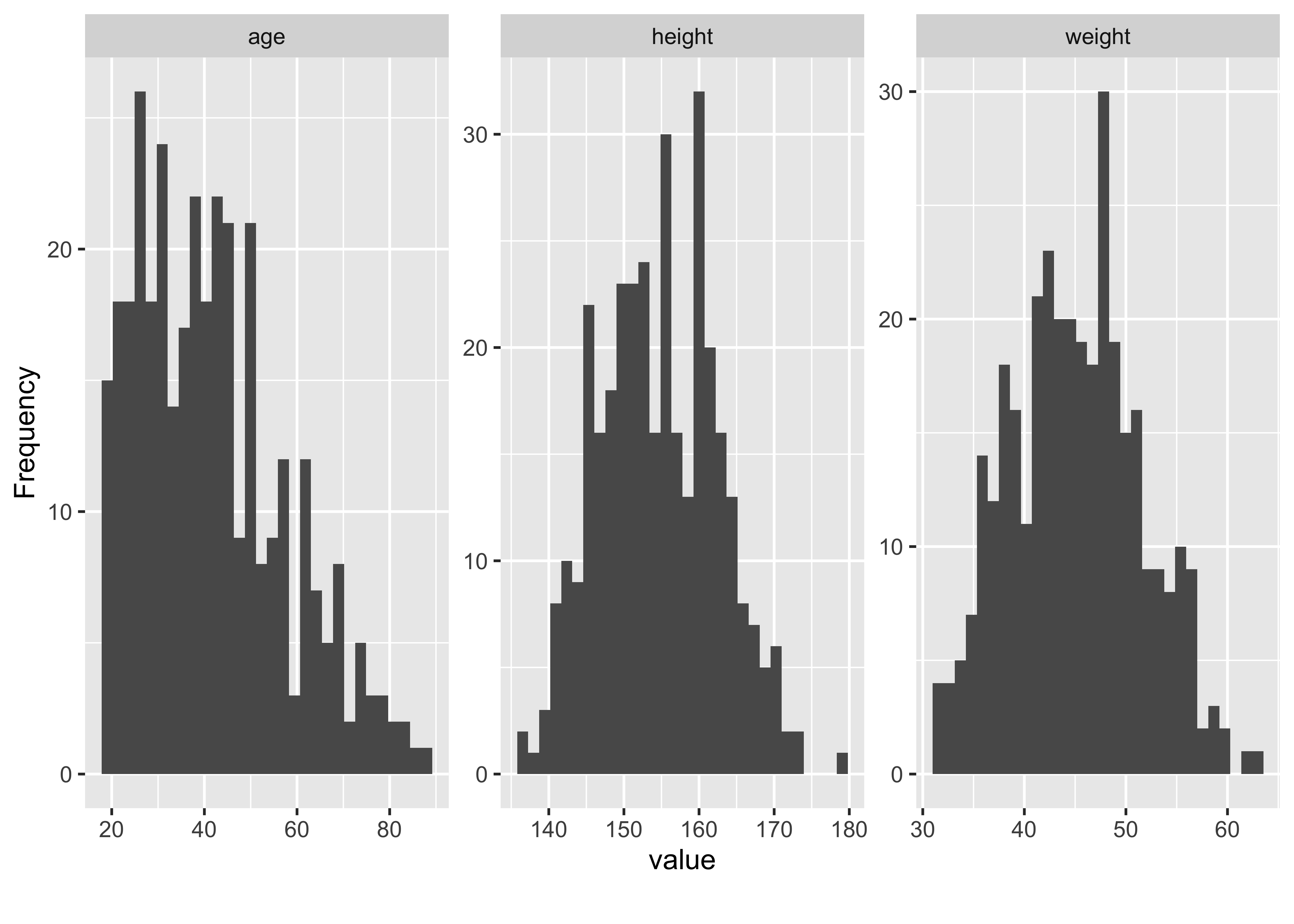
Betrachten wir als Nächstes die Verteilung der numerischen Variablen des Datensatzes, s. Abbildung 9.2.

kung_erwachsen %>% plot_histogram()

Abbildung 9.2: Verteilung (als Histogramme dargestellt) der numerischen Variablen des Datensatzes

Wie man in Abbildung 9.2 sieht, ist Alter (age) rechtsschief verteilt, wohingegen Größe (height) und Gewicht (weight) deutlich symmetrischer oder sogar normalverteilt sind. height ist bimodal (zweigipflig), vermutlich auf Grund der Vermischung der Verteilung der beiden Geschlechter.

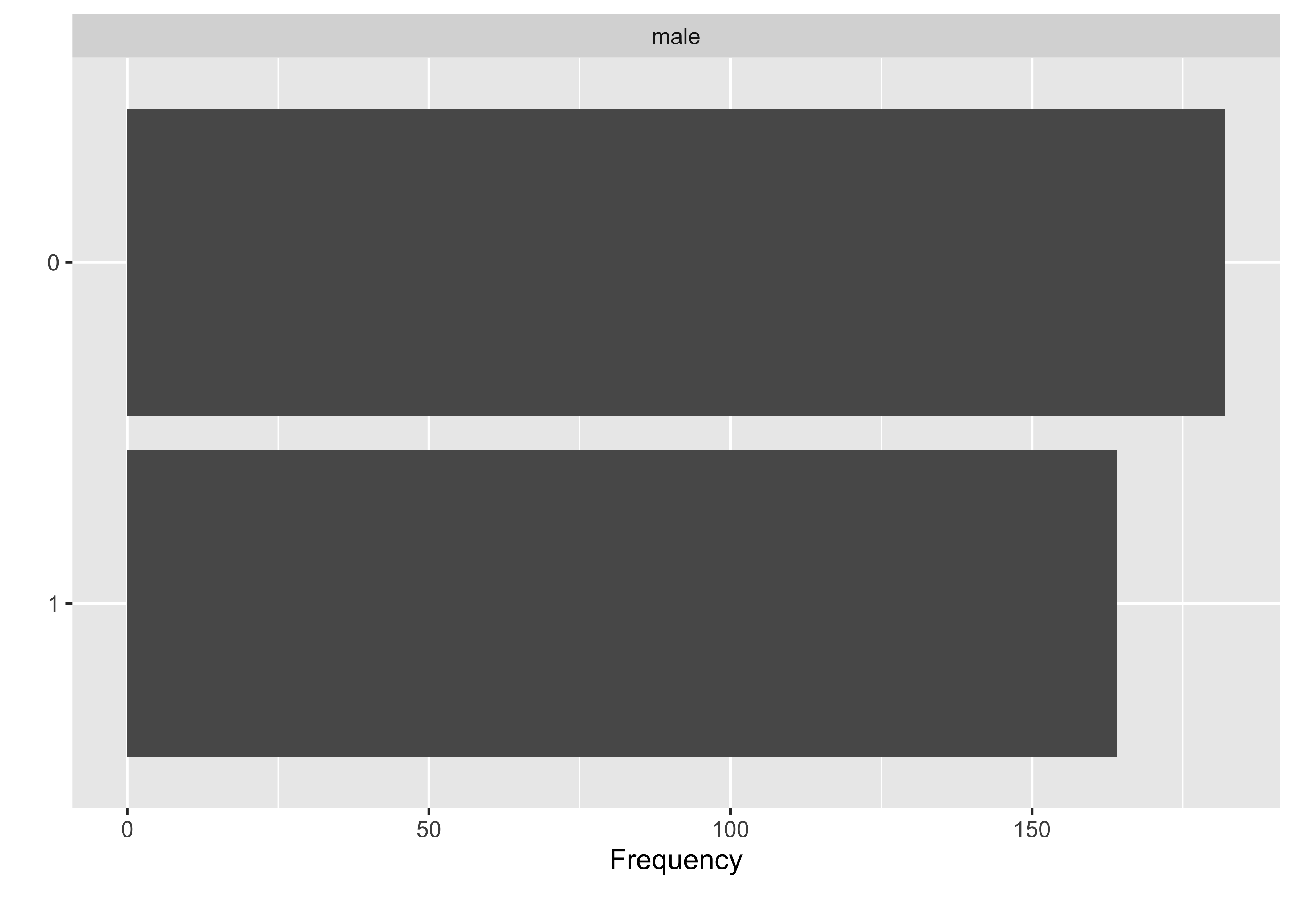
Betrachten wir nin die Verteilung der kategorialen Variablen des Datensatzes, s. Abbildung 9.3. Es gibt etwas mehr Männer als Frauen im Datensatz.

kung_erwachsen |> 
  count(male) |> 
  mutate(Anteil_maenner = n / sum(n))

ABCDEFGHIJ0123456789

male <dbl>	n <int>	Anteil_maenner <dbl>
0	182	0.53
1	164	0.47

2 rows

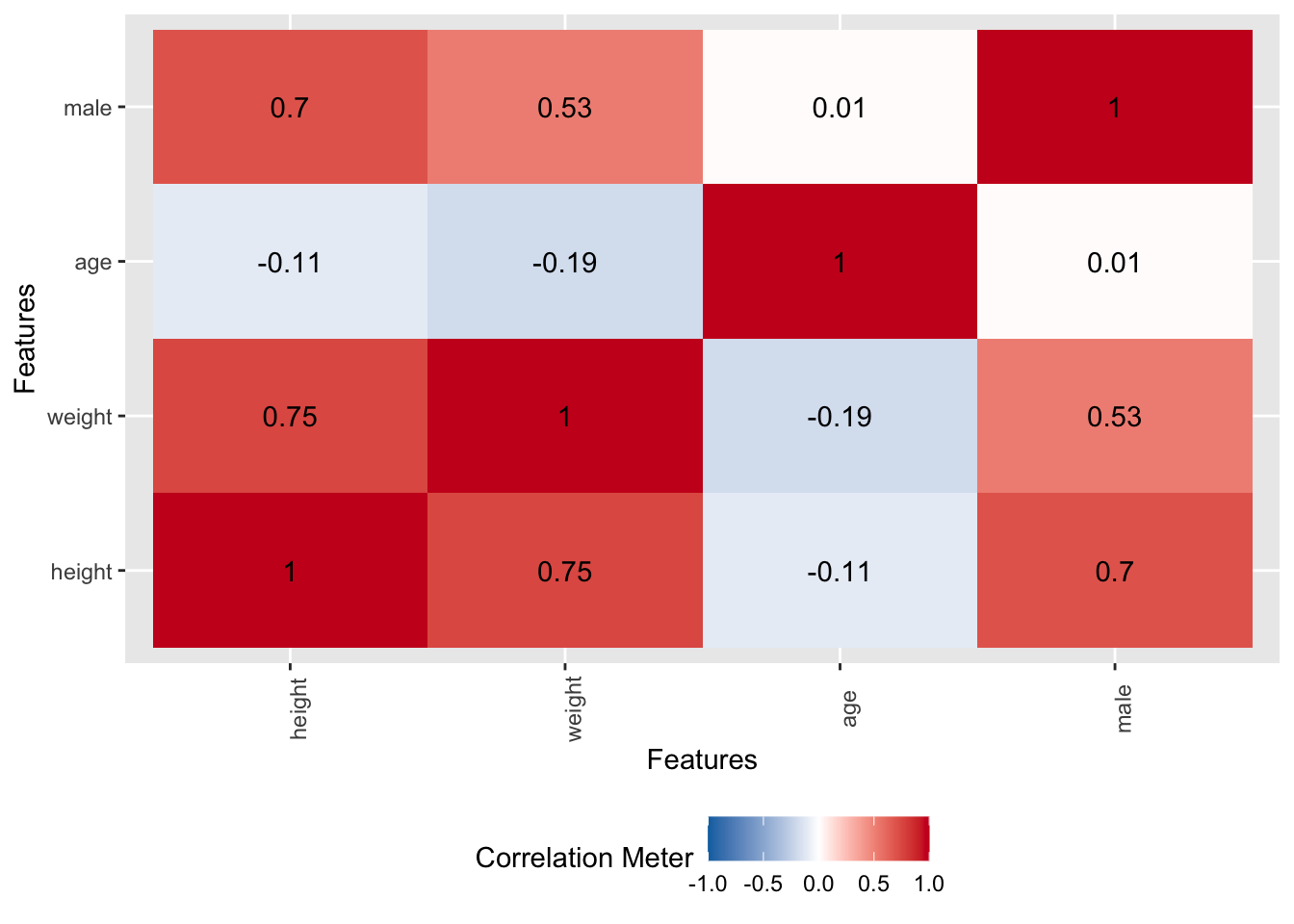
kung_erwachsen %>% plot_bar()

Abbildung 9.3: Verteilung (als Balkendiagramme dargestellt) der kategorialen Variablen des Datensatzes

Korrelationen sind, ähnlich wie Regressionen, eine Methode, um Zusammenhänge zwischen Variablen darzustellen. Allerdings sind Korrelationen nur für zwischen zwei Variablen definiert; Regressionsanalysen können komfortabel mehrere Variablen berücksichtigen. Die Korrelationen der (numerischen) Variablen sind in Abbildung 9.4 dargestellt.

kung_erwachsen %>% plot_correlation()

Abbildung 9.4: Korrelationsmatrix

Starke Zusammenhänge finden sich (wenig überraschend) zwischen Größe und Gewicht sowie zwischen Geschlecht und Größe/Gewicht.

Übungsaufgabe 9.3 (Vertiefung: EDA-Bericht) Probieren Sie mal die folgende Funktion aus, die Ihnen einen Bericht zur EDA erstellt: create_report(kung_erwachsen). $◻$

9.2.2 Der Zusammenhang von Gewicht und Größe

Die (einfache) Regression prüft, inwieweit zwei Variablen, $Y$ und $X$ linear zusammenhängen. Je mehr sie zusammenhängen, desto besser kann man $X$ nutzen, um $Y$ vorherzusagen (und umgekehrt). Hängen $X$ und $Y$ zusammen, heißt das nicht (unbedingt), dass es einen kausalen Zusammenhang zwischen $X$ und $Y$ gibt. Linear ist ein Zusammenhang, wenn der Zuwachs in $Y$ relativ zu $X$ konstant ist: wenn $X$ um eine Einheit steigt, steigt $Y$ immer um $b$ Einheiten (nicht kausal, sondern deskriptiv gemeint).²

Laden wir die !Kung-Daten und visualisieren wir uns den Zusammenhang zwischen Gewicht (X, UV) und Größe (Y, AV), Abbildung 9.5.

Mit ggplot2

kung_erwachsen %>% 
  ggplot(
       aes(x = weight, y = height)) +
  geom_point(alpha = .7) +
  geom_smooth(method = "lm")

Mit ggpubr

ggscatter(kung_erwachsen,
          x = "weight", y = "height",
          add = "reg.line") 

Abbildung 9.5: Der Zusammenhang zwischen Gewicht (X) und Größe (Y)

Wie man sieht in Abbildung 9.5, gibt es einen deutlichen linearen Zusammenhang zwischen Gewicht und Größe: Je schwerer (je höher das Gewicht einer Person), desto größer (dest höher ihr Wert in der Körpergröße).

9.2.3 Prädiktor zentrieren

Hinweis

Wenn Sie mit der z-Transformation nicht vertraut sind, macht es Sinn, das Thema (jetzt) zu lernen, s.B. hier. $◻$

Zieht man von jedem Gewichtswert den Mittelwert ab, so bekommt man die Abweichung des Gewichts vom Mittelwert; der Prädiktor ist dann zentriert, (engl. to center). Wenn man den Prädiktor Gewicht (weight) zentriert hat, ist der Achsenabschnitt, ${\beta }_0$, einfacher zu verstehen: In einem Modell mit zentriertem Prädiktor (weight) gibt der Achsenabschnitt die Größe einer Person mit durchschnittlichem Gewicht an. Würde man weight nicht zentrieren, gibt der Achsenabschnitt die Größe einer Person mit weight=0 an, was nicht wirklich sinnvoll zu interpretieren ist; vgl. Gelman et al. (2021), Kap. 10.4, 12.2. Man zentriert eine Variable $X$, indem man von $x_i$ den Mittelwert $\overline{x}$ abzieht: $x_i-\overline{x}$. Im Folgenden zentrieren wir Gewicht (weight); die resultierende Variable nennen wir weight_c (c wie “centered”).

kung_zentriert <-
  kung_erwachsen %>% 
  mutate(weight_c = weight - mean(weight))

Mit Hilfe der Funktion center() aus {easystats} kann man sich das Zentrieren erleichtern.

kung_zentriert <- 
  kung_erwachsen %>% 
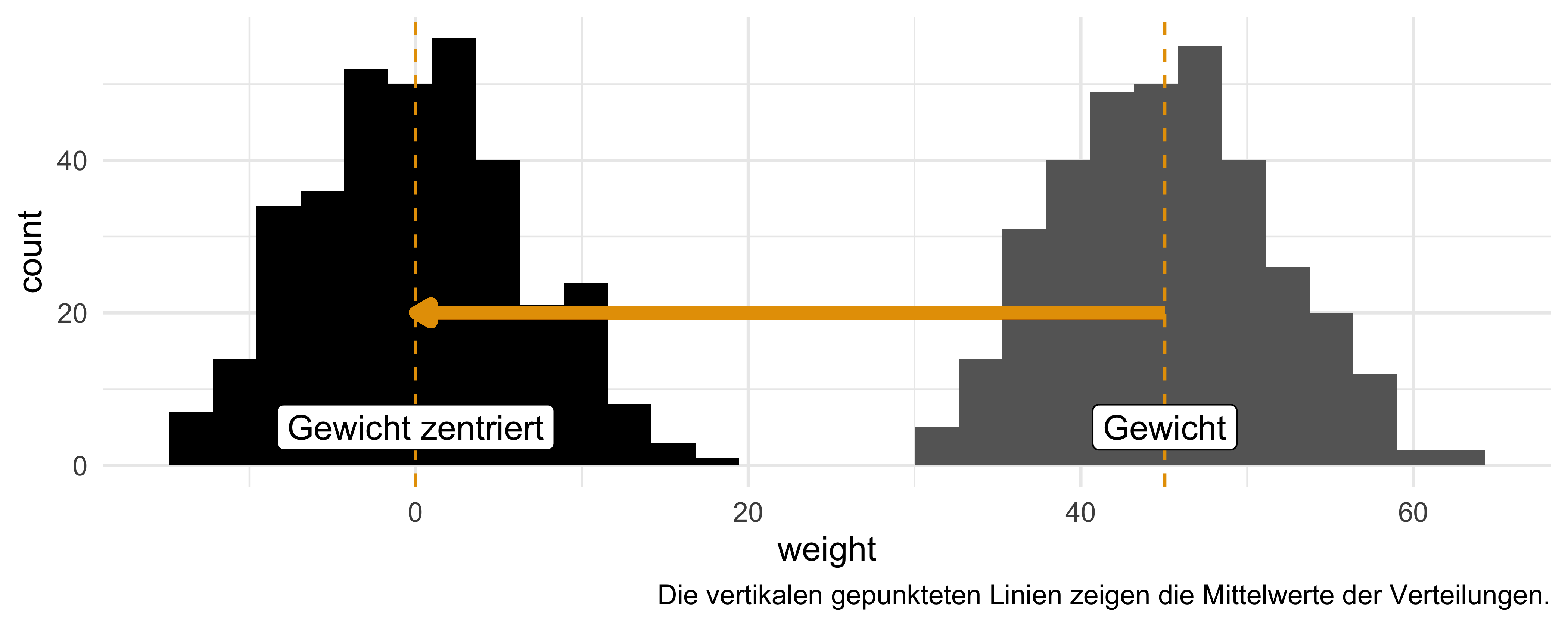
  mutate(weight_c = as.numeric(center(weight)))

Tabelle 9.2: Gewicht (weight) und zentriertes Gewicht (weight_c): Zentrierte Gewichtswerte zeigen, wie viele Kilogramm eine Person vom Mittelwert entfernt ist. So ist die Person mit der ID 1 drei Kilogramm schwerer als der Mittelwert von 45 kg.

id	weight	weight_c	height	age	male
1	48	3	152	63	1
2	36	−9	140	63	0
3	32	−13	137	65	0

Wie man sieht, wird die Verteilung von weight durch die Zentrierung “zur Seite geschoben”: Der Mittelwert von weight_c (das zentrierte Gewicht) liegt jetzt bei 0, s. Abbildung 9.6.

Abbildung 9.6: Das Zentrieren ändert die Verteilungsform nicht, sondern “schiebt” die Verteilung nur zur Seite. Der resultierende Mittelwert ist dann Null. Dier zentrierten Werte zeigen, wie weit ein Messwert vom Mittelwert entfernt ist (hier in der Einheit kg).

Das Schwierigste ist dabei nur, nicht zu vergessen, dass kung_zentriert die Tabelle mit zentriertem Prädiktor ist, nicht kung_erwachsen.

9.3 Modell m_kung_gewicht_c: zentrierter Prädiktor

📺 Prädiktoren zentrieren

Erstellen wir nun ein Regressionsmodell mit dem zentrierten Prädiktor, Gewicht. Die Forschungsfrage lautet: “Wie stark ist der lineare Zusammenhang von Größe und Gewicht?”. Anders formuliert: “Um wiele Zentimeter Körpergröße unterscheiden sich zwei erwachsene Kung, wobei die eine Person um 1 kg leichter ist als die andere?”.

Einige Regressionskoeffizienten, wie der Achsenabschnitt (engl. intercept) sind schwer zu interpretieren: Bei einem (erwachsenen) Menschen mit Gewicht 0, was wäre wohl die Körpergröße? Hm, Philosophie steht heute nicht auf der Tagesordnung. Da wäre es schön, wenn wir die Daten so umformen könnten, dass der Achsenabschnitt eine sinnvolle Aussage macht. Zum Glück geht das leicht: Wir zentrieren den Prädiktor (Gewicht)!

Wichtig

Durch Zentrieren kann man die Ergebnisse einer Regression einfacher interpretieren.

Zuerst stellen wri die Modelldefinition von m_kung_gewicht_c auf.

Für jede Ausprägung des Prädiktors Gewicht zentriert (weight_centered), $w{c}_i$, wird eine Post-Verteilung für die abhängige Variable Größe (height, $h_i$) berechnet. Der Mittelwert $\mu$ für jede Post-Verteilung ergibt sich aus dem linearen Modell (unserer Regressionsformel). Die Post-Verteilung berechnet sich auf Basis der Priori-Werte und des Likelihoods (Bayes-Formel). Wir brauchen Priori-Werte für die Steigung ${\beta }_1$ und den Achsenabschnitt ${\beta }_0$ der Regressionsgeraden. Außerdem brauchen wir einen Priori-Wert, der die Streuung $\sigma$ der Größe (height) angibt; dieser Wert wird als exponentialverteilt angenommen. Der Likelihood gibt an, wie wahrscheinlich ein bestimmter Wert height ist, gegeben $\mu$ und $\sigma$. Theorem 9.1 stellt die Modelldefinition dar. Abbildung 9.7 zeigt, wie die drei Parameter zusammen die Likelihood definieren.

Abbildung 9.7

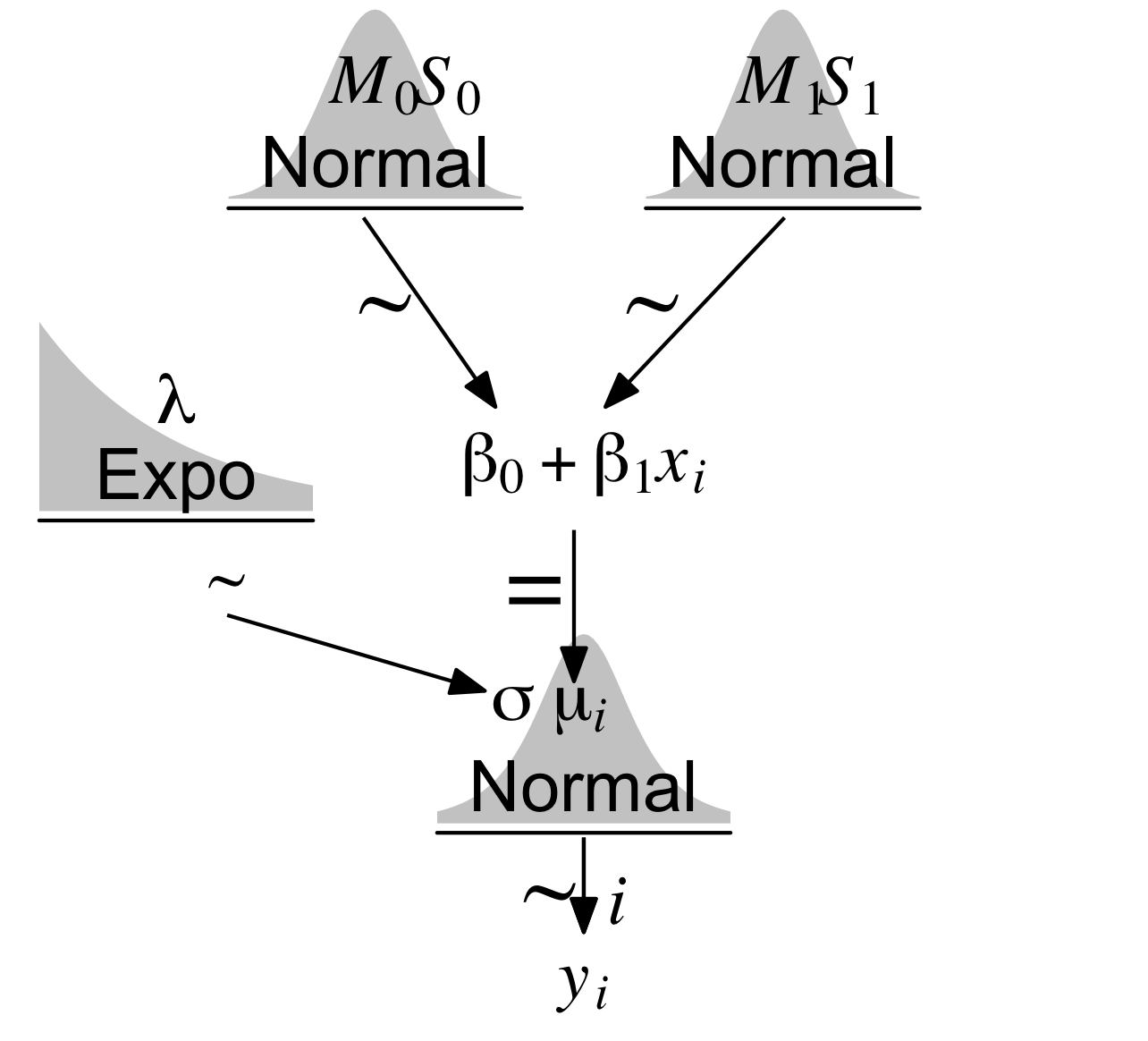
Theorem 9.1 stellt Abbildung 9.7 als Modellgleichung dar. Abbildung 9.8 zeigt anhand der Regressionsgerade, wie die vorhergesagten Körpergrößen zustande kommen: $\mu$ (vorhergesagte Körpergröße) beruht auf dem jeweiligen $X$-Wert (d.h. Gewicht, UV); zusammen mit der Streuung der Körpergrößen um den Mittelwert ($\sigma$) ergibt sich dann die Normalverteilung der Körpergrößen, $y_i$ (AV).

Abbildung 9.8: Die Körpergrößen, $Y$ (AV) sind abhängig vom Wert des Körpergewichts, $X$, (UV)

Theorem 9.1 (Modelldefinition m_kung_gewicht_c) $$\begin{array}{rlrl}{\text{height}}_i& \sim \mathrm{Normal}({\mu }_i,\sigma )& & \text{Likelihood}\\ {\mu }_i& ={\beta }_0+{\beta }_1\cdot {\text{weightcentered}}_i& & \text{Lineares Modell, Regressionsformel}\\ {\beta }_0& \sim \mathrm{Normal}(178,20)& & \text{Priori}\\ {\beta }_1& \sim \mathrm{Normal}(0,10)& & \text{Priori}\\ \sigma & \sim \mathrm{Exp}(0.1)& & \text{Priori}\end{array}◻$$

$$\begin{array}{rlrl}{\text{height}}_i& \sim \mathrm{Normal}({\mu }_i,\sigma )& & \text{Likelihood}\end{array}$$

Der Likelihood von m_kung_gewicht_c ist ähnlich zu den vorherigen Modellen (m_kung). Nur gibt es jetzt ein kleines “Index-i” am $\mu$ und am $h$ (h wie heights). Es gibt jetzt nicht mehr nur einen Mittelwert $\mu$, wie in m_kung, sondern für jede Beobachtung (Zeile) einen Mittelwert ${\mu }_i$. Lies etwa so:

“Die Wahrscheinlichkeit, eine bestimmte Größe $h$ bei Person $i$ zu beobachten, gegeben $\mu$ und $\sigma$ ist normalverteilt (mit Mittelwert $\mu$ und Streuung $\sigma$)”.

Betrachten wir als nächstes die Regressionsformel, m_kung_gewicht_c:

$$\begin{array}{rlrl}{\mu }_i& ={\beta }_0+{\beta }_1\cdot {\text{weightcentered}}_i& & \text{Lineares Modell}\end{array}$$

$\mu$ ist jetzt nicht mehr ein Parameter, der (stochastisch) geschätzt werden muss (wie in m_kung). $\mu$ wird jetzt (deterministisch) berechnet. Gegeben ${\beta }_0$ und ${\beta }_1$ ist $\mu$ also ohne Ungewissheit bekannt. ${\text{weight}}_i$ ist der Gewichtswert (weight) der $i$ten Beobachtung, also einer !Kung-Person (Zeile $i$ im Datensatz). Lies etwa so:

“Der vorhergesagte mittlere Wert der Körpergröße, ${\mu }_i$, der $i$ten Person berechnet sich als Summe von ${\beta }_0$ und ${\beta }_1$ mal ${\text{weight}}_i$”.

${\mu }_i$ ist eine lineare Funktion von weight. ${\beta }_1$ gibt den Unterschied in height zweier Beobachtung an, die sich um eine Einheit in weight unterscheiden (Steigung der Regressionsgeraden). ${\beta }_0$ gibt an, wie groß $\mu$ ist, wenn weight Null ist (Achsenabschnitt, engl. intercept).

Was sind unsere Priori-Verteilung des Modells m_kung_gewicht_c? Sie gleichen denen von m_kung, allerdings haben wir jetzt zusätzlich ${\beta }_1$. Dieser Parameter gibt die Steigung der Regressionsgeraden an (auch als “Regressiongsgewicht” bezeichnet). Damit wird die Stärke des (linearen) Zusammenhangs zwischen UV (X) und AV (Y) festgelegt. Hier definieren wir den Zusammenhang als normalverteilt mit Mittelwert 0 und Streuung 10 cm. Damit liegt der Bereich plausibler Werte für den Zusammenhang von Gewicht und Größe zwischen -20 cm bis +20 cm Unterschied in der Körpergröße pro Kilogramm Unterschied im Körpergewicht. Das ist ein recht informationsarmer Wert: Viele Werte sind möglich, auch unerwartete. Man kann argumentieren, dass diese Apriori-Verteilung biologisch nicht realistisch ist. Dazu später mehr.

$$\begin{array}{rlrl}{\beta }_0& \sim \mathrm{Normal}(178,20)& & \text{Priori Achsenabschnitt}\\ {\beta }_1& \sim \mathrm{Normal}(0,10)& & \text{Priori Regressionsgewicht}\\ \sigma & \sim \mathrm{Exp}(0.1)& & \text{Priori Sigma}\end{array}$$

Parameter sind hypothetische Kreaturen: Man kann sie nicht beobachten, sie existieren nicht wirklich. Ihre Verteilungen nennt man Priori-Verteilungen. ${\beta }_0$ wurde in m_kung als $\mu$ bezeichnet, da wir dort eine “Regression ohne Prädiktoren” berechnet haben. $\sigma$ ist uns schon als Parameter bekannt und behält seine Bedeutung aus dem letzten Kapitel. Da height nicht zentriert ist, der Mittelwert von ${\beta }_0$ bei 178 und nicht 0. ${\beta }_1$ fasst unser Vorwissen, ob und wie sehr der Zusammenhang zwischen Gewicht und Größe positiv (gleichsinnig) ist. ${\beta }_1$ ist hier schwach informativ: Im Schnitt, behauptet diese Apriori-Verteilunng, sei der Zusammenhang gleich Null. Aber die Apriori-Verteilung akzeptiert auch recht starke positive und negative (!) Werte. Diese Wahl an Apriori-Werten ist nicht unbedingt ideal. Wir sollten uns künftig noch andere (bessere) Parameter für die Apriori-Verteilung von ${\beta }_1$ überlegen. Die Anzahl der Prioris entspricht übrigens der Anzahl der Parameter des Modells.

Jetzt sind wir bereit, das Model bzw. die Post-Verteilung zu berechnen. Erinnern wir uns: “Prioris plus Daten gleich Post”. Los, Stan, an die Arbeit! Berechne uns die Post-Verteilung. Nennen wir das Modull m_kung_gewicht_c.

m_kung_gewicht_c <-
  stan_glm(
    height ~ weight_c,  # Regressionsformel
    prior = normal(0, 10),  # Regressionsgewicht (beta 1)
    prior_intercept = normal(178, 20),  # beta 0
    prior_aux = exponential(0.1),  # sigma
    refresh = 0,  # zeig mir keine Details
    data = kung_zentriert)

parameters(m_kung_gewicht_c)

parameters(m_kung_gewicht_c) |> display()

Tabelle 9.3: Parameter von m_kung_gewicht_c

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	154.65	(154.11, 155.19)	100%	1.000	3778	Normal (178 +- 20)
weight_c	0.91	(0.83, 0.99)	100%	1.001	4030	Normal (0 +- 10)

Wie man in Tabelle 9.3 sieht, wird der Zusammenhang von Gewicht und Größe, d.h. ${\beta }_1$, die Steigung der Regressionsgeraden, auf einen Wert zwischen ca. 0.8 bis 1.0 kg Unterschied in der Körpergröße geschätzt (wenn sich die Personen um 1 kg Körpergewicht unterscheiden). Es gibt also einen Zusammenhang zwischen Gewicht und Größe (laut unserem Modell). Danke, Stan!

Übungsaufgabe 9.4 (Peer-Instruction: Wie leitet sich der Wert der Körpergrößen $h_i$ her?) Welche Aussage zur Herleitung der Körpergrößen, $h_i$, ist korrekt?

• Die Körpergrößen sind gleich mit dem um das Regressionsgewicht gewichteten Wert des jeweiligen Körpergewichts (d.h. $h_i={\beta }_1\cdot w{c}_i$).
• Die Körpergrößen sind apriori normalverteilt mit dem Mittelwert 178 cm (in diesem Modell).
• Die Körpergrößen sind apriori normalverteilt mit dem Mittelwert, der sich aus dem Regressionsmodell ergibt für jede Beobachtung $i$.
• Die Körpergrößen sind das Resultat zweier Parameter: Der mittleren Körpergröße, $\mu$, sowie der Streuung in der Population, $\sigma$. $◻$

9.4 Die Post-Verteilung befragen

📺 Post-Verteilung auslesen 1

📺 Post-Verteilung auslesen 2

9.4.1 m_kung_starkes_beta1

Mit der Apriori-Verteilung von $bet{a}_1$ in m_kung_gewicht_c sind wir nicht zufrieden. Sagen wir stattdessen, auf Basis gut geprüfter Evidenz haben wir folgendes Modell festgelegt: height ~ weight_c, s. Gleichung 9.1. Dabei haben wir folgende Apriori-Verteilungen gewählt:

$$\begin{gathered} \begin{array}{}\text{(9.1)}& {\beta }_1\sim N(5,3); \\ {\beta }_0\sim N(178,20); \\ \sigma \sim E(0.1)\end{array} \end{gathered}$$

Dieses Mal haben wir für ${\beta }_1$ durchaus “meinungsstarke” Werte ausgewählt. Im Schnitt gehen wir von einem Zusammenhang aus, so dass es einen Unterschied von 5 cm in der AV (Größe) gibt, wenn sich die UV (Gewicht) um 1 Einheit (1 kg) unterscheidet zwischen zwei Personen. Wir nennen das Modell m_kung_starkes_beta1³, s. Listing 9.1.

Listing 9.1: Modelldefinition von m_kung_starkes_beta1 in R

m_kung_starkes_beta1 <-
  stan_glm(
    height ~ weight_c,  # Regressionsformel
    prior = normal(5, 3),  # Regressionsgewicht (beta 1)
    prior_intercept = normal(178, 20),  # beta 0
    prior_aux = exponential(0.1),  # sigma
    refresh = 0,  # zeig mir keine Details
    data = kung_zentriert)

Hinweis

Mit seed kann man die Zufallszahlen fixieren, so dass jedes Mal die gleichen Werte resultieren. So ist die Nachprüfbarkeit der Ergebnisse (“Reproduzierbarkeit”) sichergestellt⁴. Welche Wert für seed man verwendet, ist egal, solange alle den gleichen verwenden. Der Autor verwendet z.B. oft den Wert 42. Zur Erinnerung: Der Golem zieht Zufallszahlen, damit erstellt er Stichproben, die die Postverteilung schätzen. Das Argument seed ist nur relevant, wenn man die Ergebnisse von Stan zwischen zwei Durchläufen vergleichen möchte. Ansonsten hat es keine Bedeutung.

9.4.2 Mittelwerte von ${\beta }_0$ und ${\beta }_1$ aus der Post-Verteilung

Betrachten wir die ersten paar Zeilen aus der Post-Verteilung, s. Tabelle 9.4. Dazu wandeln wir das Ergebnis-Objekt von stan_glm, d.h. m_kung_starkes_beta1 in eine Tablle (einen “Tibble”) um.

Listing 9.2: Die Post-Verteilung bekommen wir, indem wir das Ergebnisobjekt von stan_glm in einen Tibble (Dataframe) umwandeln.

m_kung_starkes_beta1_post <- 
m_kung_starkes_beta1 %>% 
  as_tibble() %>% 
  head()

Tabelle 9.4: Die ersten paar Zeilen der Post-Verteilung von m_kung_starkes_beta1

id	(Intercept)	weight_c	sigma
1	155.1	0.9	5.0
2	155.5	0.8	5.1
3	155.5	0.9	5.1

Tabelle 9.5 zeigt die Zusammenfassung der Stichproben aus der Post-Verteilung; komfortabel zu erhalten mit dem Befehle parameters(m_kung_starkes_beta1).

Tabelle 9.5: Parameter von m_kung_starkes_beta1

Parameter	Median	95% CI	pd	Rhat	ESS	Prior
(Intercept)	154.65	(154.14, 155.19)	100%	0.999	3214	Normal (178 +- 20)
weight_c	0.91	(0.82, 0.99)	100%	1.001	4134	Normal (5 +- 3)

Definition 9.1 (Effektwahrscheinlichkeit) Die Kennzahl pd (propability of direction) gibt die Effektwahrscheinlichkeit an: Die Wahrscheinlichkeit, dass der Effekt positiv (also größer als Null) oder negativ ist (je nachdem ob der Median des Effekts positiv oder negativ ist). pd gibt aber nicht an, wie stark der Effekt ist, nur ob er klar auf einer Seite der Null liegt. Damit ist er so etwas (grob!) Ähnliches wie der p-Wert in der Frequentistischen Statistik (Makowski et al., 2019). $◻$

Am besten das Diagramm zur Effektwahrscheinlichkeit (pd) anschauen, s Abbildung 9.9. Rhat und ESS sind Kennzahlen, die untersuchen, ob mit der Stichprobenziehung im Bayes-Modell alles gut funktioniert hat. Bei einfachen Modellen (die wir hier berechnen) sollte da in der Regel alles in Ordnung sein. Rhat sollte nicht (viel) größer als 1 oder 1,01 sein. ESS (effective sample size) gibt die Anzahl der effektiv nutzbaren Stichproben an (im Standard werden 4000 berechnet). Die Zahl sollte nicht deutlich geringer sein. Wir werden uns aber mit diesen beiden Kennwerten nicht weiter beschäftigen in diesem Kurs.

plot(p_direction(m_kung_starkes_beta1))

Abbildung 9.9: Diagramm zur Probability of Direction, Modell m_kung_starkes_beta1

9.4.3 Visualisieren der “mittleren” Regressiongeraden

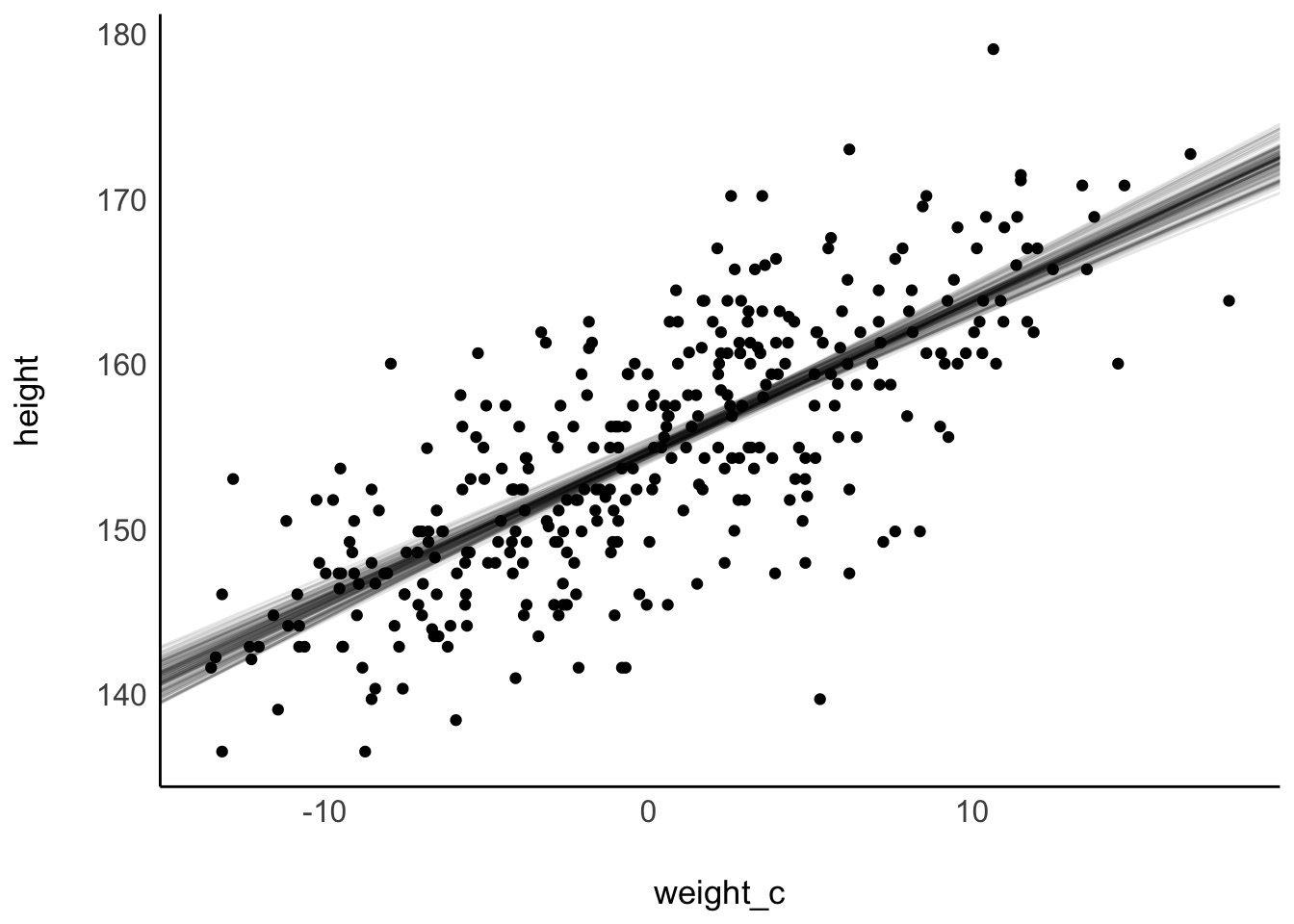
Zur Erinnerung: Die Bayes-Analyse liefert uns viele Stichproben zu den gesuchten Parametern, hier ${\beta }_0$, ${\beta }_1$ und $\sigma$. Überzeugen wir uns mit einem Blick in die Post-Verteilung von m_kung_starkes_beta1, s. Tabelle 9.4. Wir können z.B. ein Lagemaß wie den Median hernehmen, um die “mittlere” Regressionsgerade zu betrachten, s. Abbildung 9.10.

kung_zentriert %>% 
  ggplot() +
  aes(x = weight_c, y = height) +
  geom_point() +
  geom_abline(
    slope = 0.9,  # Median beta 1
    intercept = 154,  # Median beta 0
    color = "blue")

Abbildung 9.10: Die mittlere Regressionsgerade, unser ‘Best-Guess’ zum Zusammenhang von Gewicht und Größe

9.4.4 Zentrale Statistiken zu den Parametern

In diesem Modell gibt es drei Parameter: ${\beta }_0,{\beta }_1,\sigma$.⁵ Hier folgen einige Beispiele an Fragen, die wir an unser Modell bzw. die Post-Verteilung stellen können.

9.4.4.1 Lagemaße zu den Parametern

• Was ist die mittlere Größe der erwachsenen Kung? (Das war die Forschungsfrage des letzten Kapitels; ${\beta }_0$)
• Was ist der Schätzwert für den Zusammenhang von Gewicht und Größe? (${\beta }_1$)
• Was ist der Schätzwert für Ungewissheit in der Schätzung der Größe? ($\sigma$)
• Was ist der wahrscheinlichste und der mediane Wert für ${\beta }_1$?

Eine nützliche Zusammenfassung der Post-Verteilung bekommt man mit parameters(modell), s. Tabelle 9.5. Wandelt man das Ausgabe-Objekt der Bayes-Regression, d.h. m_kung_starkes_beta1, mit as_tibble() in eine Tabelle um, so bekommt man eine Tabelle mit den Stichproben der Post-Verteilung, s. Tabelle 9.4.

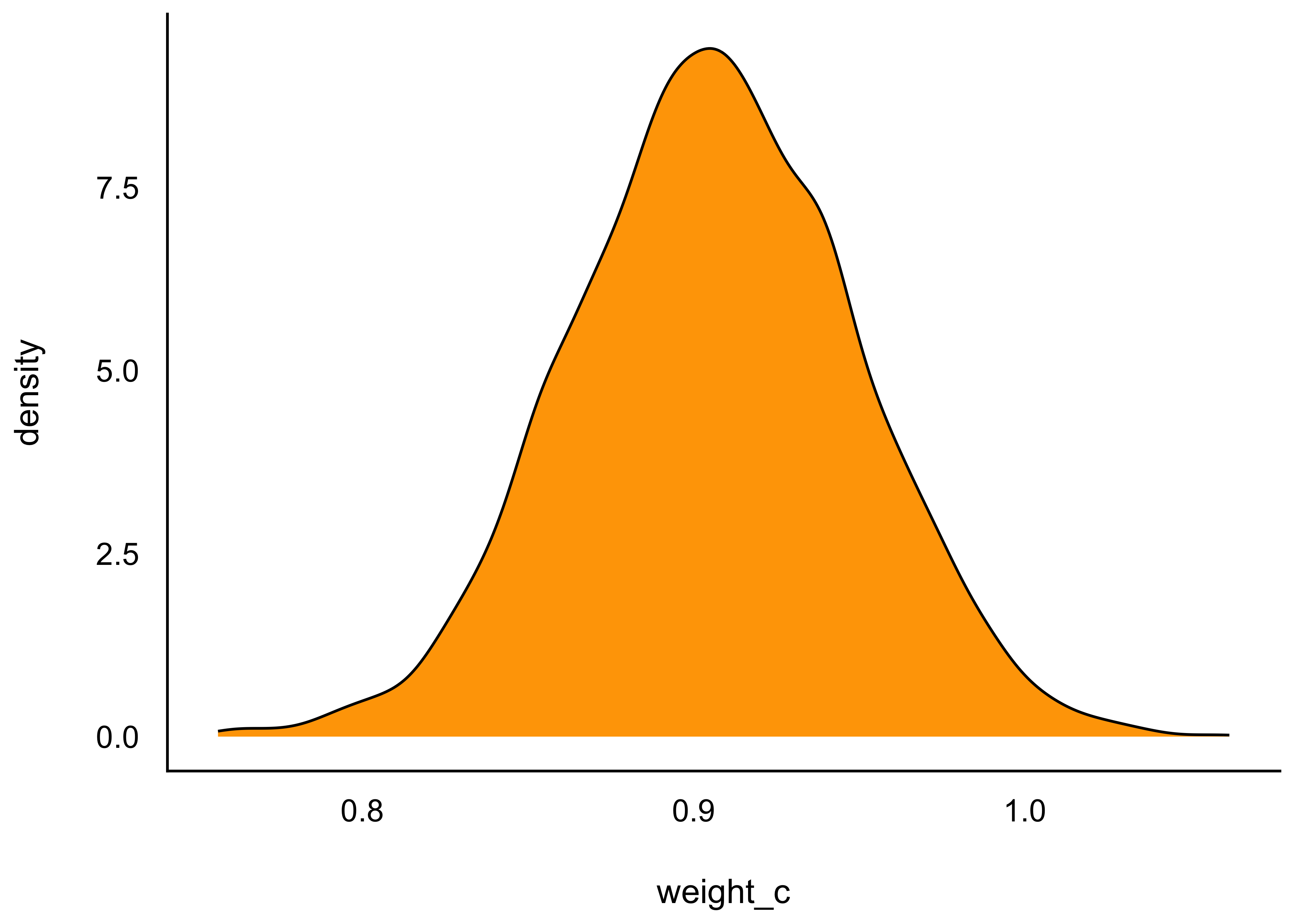
Wie wir gesehen haben, nutzen wir diese Tabelle der Post-Verteilung immer wieder. Daher haben wir sie uns als ein Objekt abgespeichert, m_kung_starkes_beta1_post, s. Listing 9.2. Jetzt haben wir wieder eine schöne Tabelle mit Stichproben aus der Post-Verteilung, die wir wie gewohnt befragen können. Oder man erstellt selber ein Diagramm mit ggplot oder ggpubr, s. Abbildung 9.11, um einen Überblick über Lage- und Streuungsmaße der Post-Verteilung zu bekommen.

m_kung_starkes_beta1_post %>% 
  ggplot(aes(x = weight_c)) +
  geom_density(fill = "orange")

Abbildung 9.11: Die Postverteilung für den Parameter Gewicht (zentriert); die plausiblen Werte liegen zwischen 0.8 und 1.0 cm pro Kilogramm Gewicht

Abbildung 9.11 zeigt, dass Mittelwert, Median und Modus eng zusammenliegen. Zur Erinnerung: Der Modus gibt den häufigsten, d.h. hier also den wahrscheinlichsten, Wert an. Der Modus wird hier auch Maximum a Posteriori (MAP) genannt, daher:

m_kung_starkes_beta1_post %>% 
  summarise(map_b1 = map_estimate(weight_c))

Hier ist die Verteilung von $\sigma$ visualisiert, s. Abbildung 9.12. Interessanterweise ist die Post-Verteilung von $\sigma$ normalverteilt und nicht mehr exponentialverteilt, wie in der Apriori-Verteilung: Die Daten haben die Apriori-Verteilung “überstimmt”.

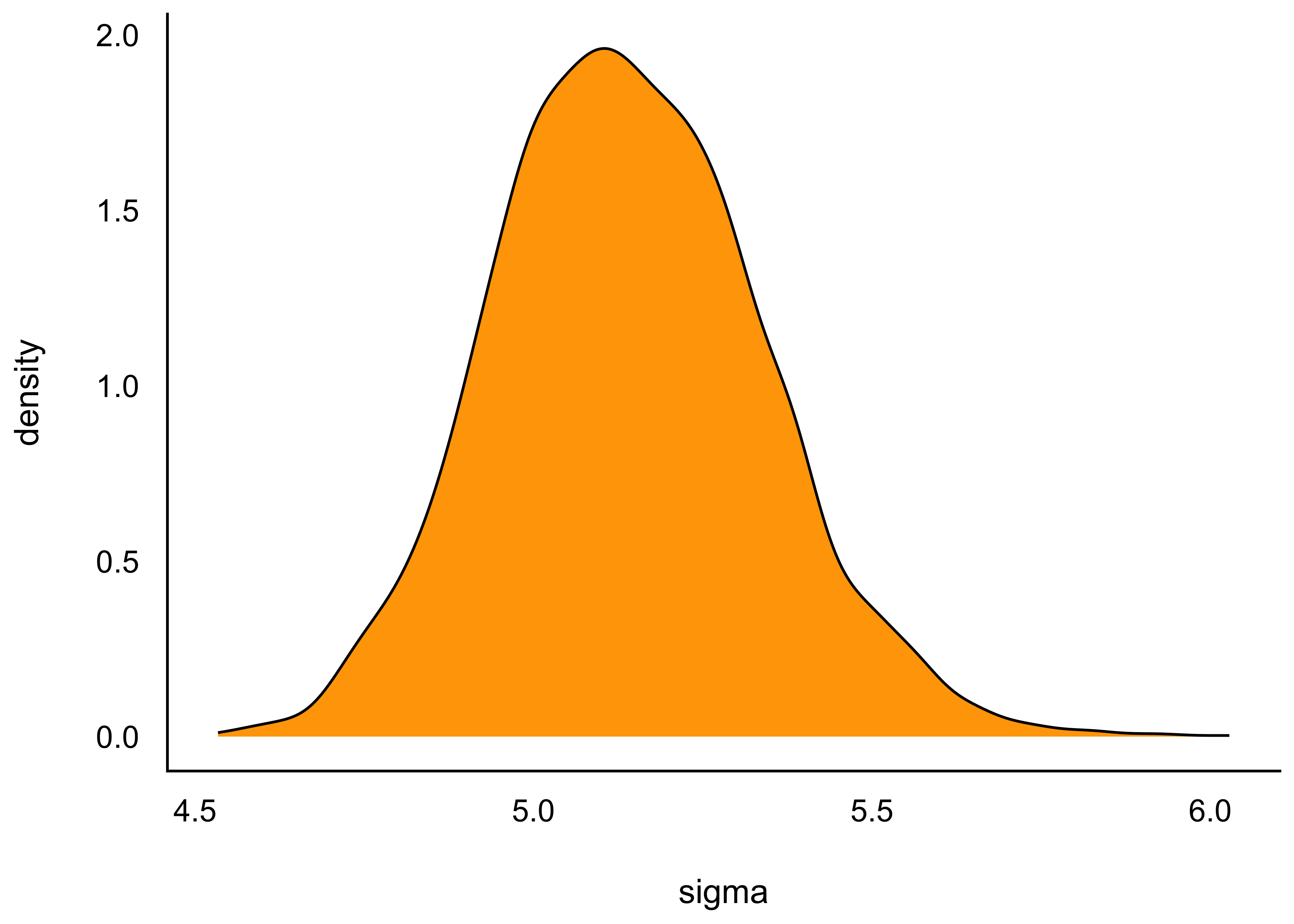
m_kung_starkes_beta1_post %>% 
  ggplot(aes(x = sigma)) +
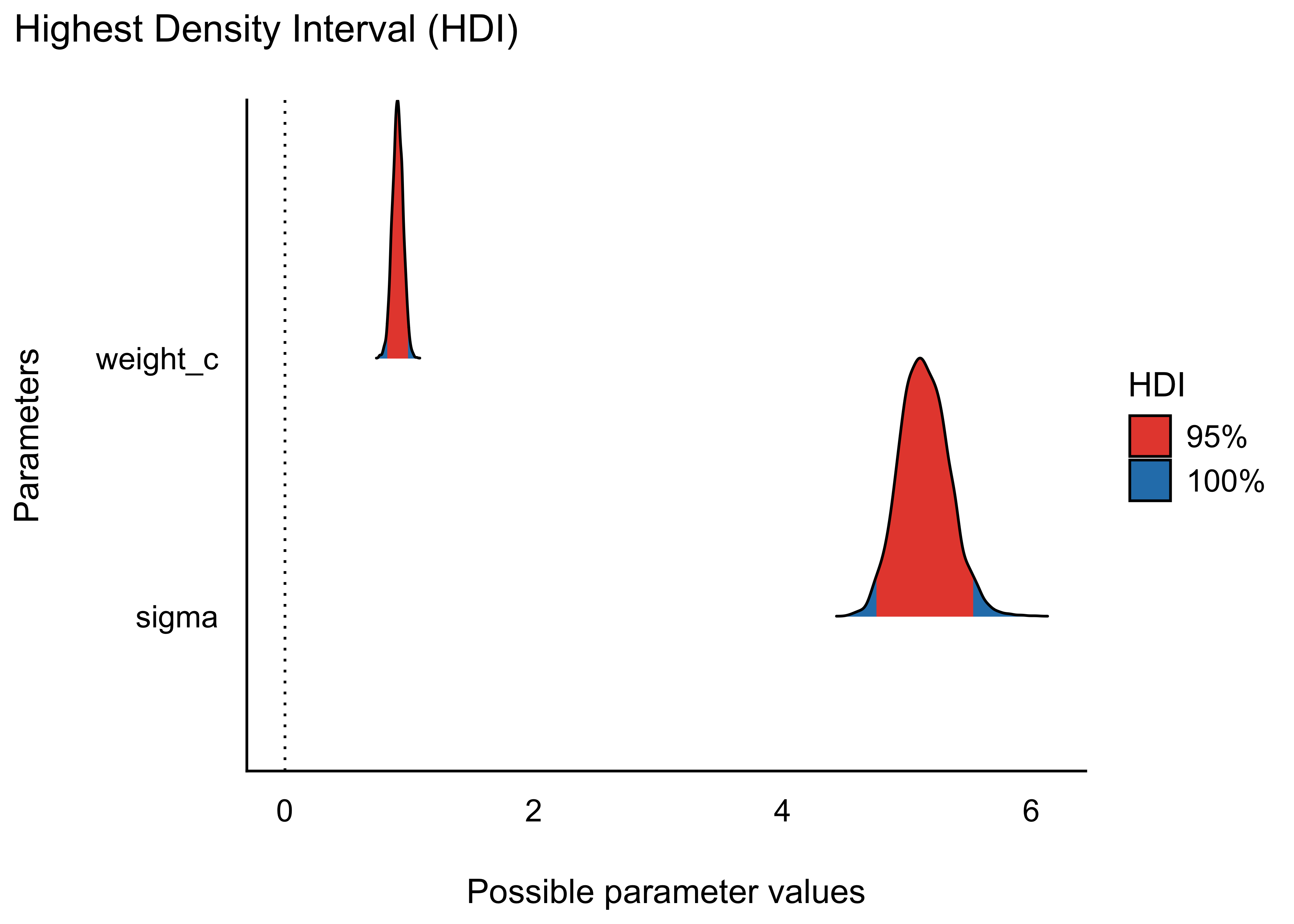
  geom_density(fill = "orange")

Abbildung 9.12: Die Post-Verteilung für den Parameter sigma, m_kung_starkes_beta1; die plausiblen Werte liegen zwischen 4.7 cm und 5.5 cm.

Alternativ kann man sich die Verteilung eines Parameters auch so ausgeben lassen, gleich mit Intervallgrenzen, z.B. 95%, s. Abbildung 9.13.

m_kung_starkes_beta1_hdi <- 
  m_kung_starkes_beta1_post |> 
  select(weight_c) |>  # analog für `select(sigma)`
  hdi()   # analog mit eti()

plot(m_kung_starkes_beta1_hdi, data = m_kung_starkes_beta1_post)

Abbildung 9.13: Die Parameter Gewicht (zentriert) Modells m_kung_starkes_beta1

Ergänzt man bei plot() noch show_intercept = TRUE wird auch der Achsenabschnitt angezeigt. Den Parameter der Vorhersage-Genauigkeit, $\sigma$ bekommt man mit get_sigma:

get_sigma(m_kung_starkes_beta1)
## [1] 5.1
## attr(,"class")
## [1] "insight_aux" "numeric"

9.4.5 Streuungsmaße zu den Parametern

• Wie unsicher sind wir uns in den Schätzungen der Parameter?

Diese Frage wird durch die Ungewissheitsintervalle in der Ausgabe beantwortet.

Hinweis

An einigen Stellen wird empfohlen, anstelle eines (gebräuchlichen) 95%-Intervalls auf ein 90%- oder 89%-Intervall auszuweichen, aufgrund der besseren numerischen Stabilität.

9.4.6 Ungewissheit von ${\beta }_0$ und ${\beta }_1$ aus der Post-Verteilung visualisiert

Abbildung 9.14 stellt die Ungewissheit der Post-Verteilung dar, in dem einige Stichproben aus der Post-Verteilung visualisiert werden.

10

Die ersten 10 Stichproben:

kung_zentriert %>% 
  ggplot(aes(x = weight_c, 
             y = height)) +
  geom_point() +
  geom_abline(
    data = m_kung_starkes_beta1_post %>% 
      slice_head(n = 10),
    aes(slope = weight_c,
        intercept = `(Intercept)`),
    alpha = .3)

100

Die ersten 100 Stichproben:

kung_zentriert %>% 
  ggplot(aes(x = weight_c, 
             y = height)) +
  geom_point() +
  geom_abline(
    data = m_kung_starkes_beta1_post %>% 
      slice_head(n = 100),
     aes(slope = weight_c,
        intercept = `(Intercept)`),
    alpha = .1)

1000

Die ersten 1e3 Stichproben:

kung_zentriert %>% 
  ggplot(aes(x = weight_c, 
             y = height)) +
  geom_point() +
  geom_abline(
    data = m_kung_starkes_beta1_post %>% 
      slice_head(n = 1e3),
     aes(slope = weight_c,
        intercept = `(Intercept)`),
    alpha = .01)

1000000

Die ersten 1000000⁶ … okay, lassen wir es gut sein⁷.

Abbildung 9.14

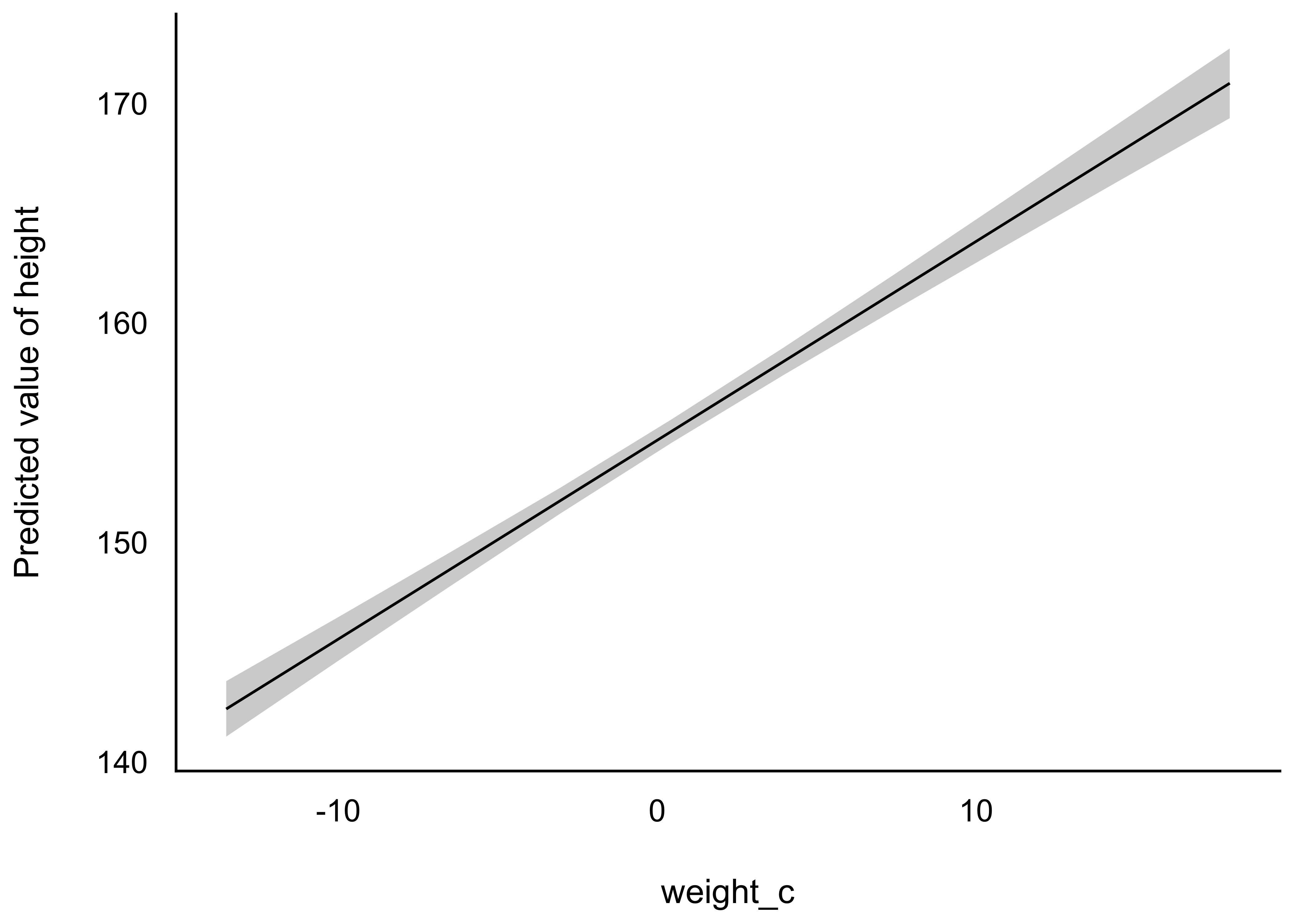
Einfacher ist die Visualisierung mit estimate_expectation, s. Abbildung 9.15.

estimate_expectation(m_kung_starkes_beta1, by = "weight_c") %>%  # Regressionsgerade
  plot() +
  geom_point(data = kung_zentriert, aes(x = weight_c, y = height)) # Punkte

Abbildung 9.15: Schätzbereich für die bedingten mittleren Körpergröße, also die Regressionsgerade mit Unsicherheitsintervall

9.4.7 Fragen zu Quantilen des Achsenabschnitts

Hinweis

Zur Erinnerung: Bei einem zentrierten Prädiktor misst der Achsenabschnitt die mittlere Größe⁸.

• Welche mittlere Größe wird mit einer Wahrscheinlichkeit von 50%, 90% bzw. 95% Wahrscheinlichkeit nicht überschritten?
• Welche mittlere Größe mit Wahrscheinlichkeit von 95% nicht unterschritten?
• Von wo bis wo reicht der innere 50%-Schätzbereich (ETI) der mittleren Körpergröße?

Quantile:

m_kung_starkes_beta1_post %>% 
  summarise(
    q_50 = quantile(`(Intercept)`, prob = .5),
    q_90 = quantile(`(Intercept)`, prob = .9),
    q_05 = quantile(`(Intercept)`, prob = .95))

ABCDEFGHIJ0123456789

q_50 <dbl>	q_90 <dbl>	q_05 <dbl>
155	155	155

1 row

50%-ETI:

m_kung_starkes_beta1 %>% 
  eti(ci = .5)

ABCDEFGHIJ0123456789

	Parameter <chr>	CI <dbl>	CI_low <dbl>	CI_high <dbl>	Effects <chr>	Component <chr>
1	(Intercept)	0.5	154.46	154.84	fixed	conditional
2	weight_c	0.5	0.88	0.94	fixed	conditional

2 rows

9.4.8 Fragen zu Wahrscheinlichkeitsmassen des Achsenabschnitts

Wie wahrscheinlich ist es, dass die mittlere Größe bei mind. 155 cm liegt?

m_kung_starkes_beta1_post %>% 
  count(gross = `(Intercept)` >= 155) %>% 
  mutate(prop = n / sum(n))

ABCDEFGHIJ0123456789

gross <lgl>	n <int>	prop <dbl>
FALSE	3593	0.9
TRUE	407	0.1

2 rows

Die Wahrscheinlichkeit beträgt 0.1.

Wie wahrscheinlich ist es, dass die mittlere Größe höchstens 154.5 cm beträgt?

m_kung_starkes_beta1_post %>% 
  count(klein = (`(Intercept)` <= 154.5)) %>% 
  mutate(prop = n / sum(n))

ABCDEFGHIJ0123456789

klein <lgl>	n <int>	prop <dbl>
FALSE	2833	0.71
TRUE	1167	0.29

2 rows

Die Wahrscheinlichkeit beträgt 0.29.

Beispiel 9.1 (Typischer Bayes-Nutzer in Aktion)  

Typischer Bayes-Nutzer, der ein Ungewissheitsintervall berechnet. Bildquelle: Easystats, bayestestR

Quelle $◻$

9.5 Post-Verteilung bedingt auf einen Prädiktorwert

9.5.1 Bei jedem Prädiktorwert eine Post-Verteilung für $\mu$

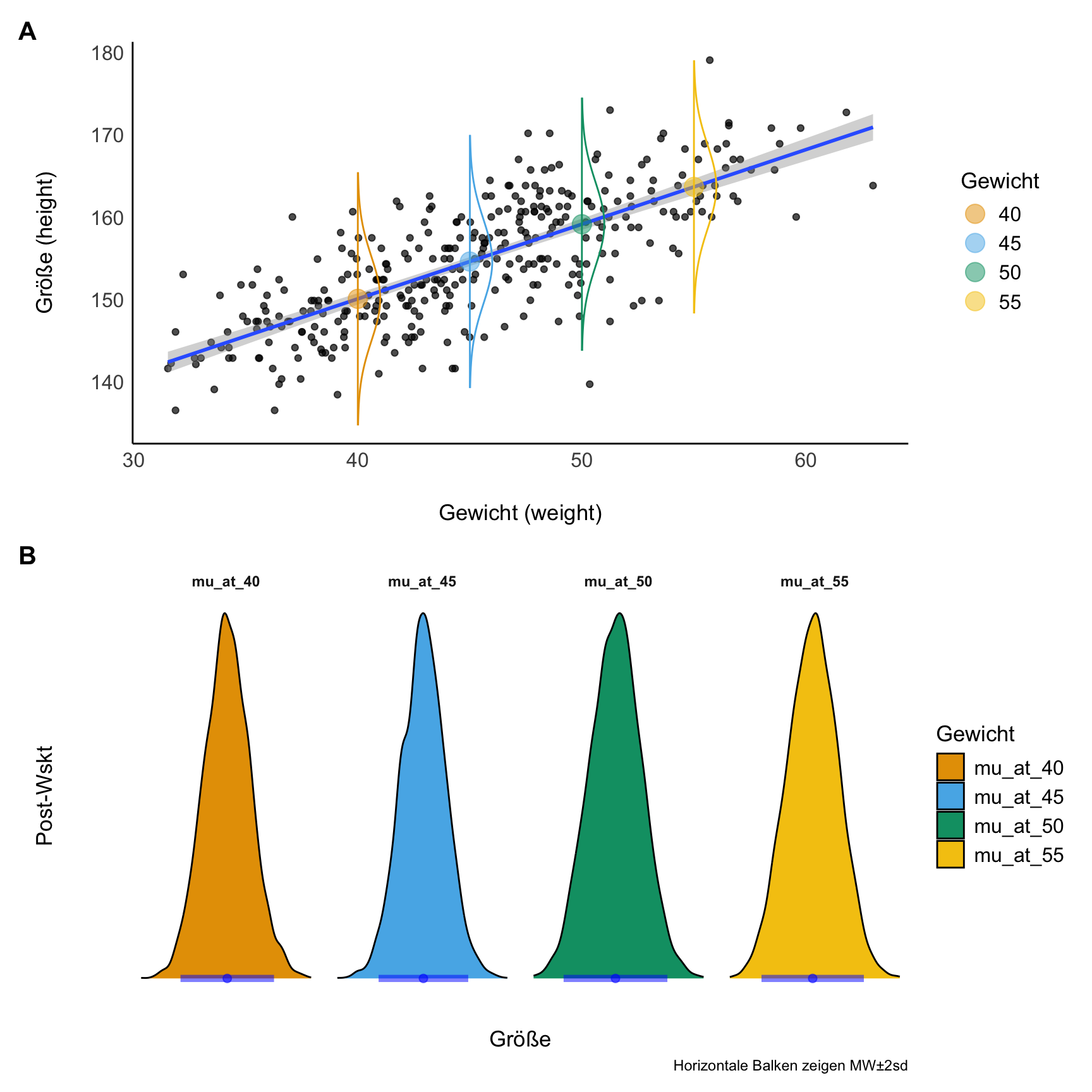
Komfort pur: Unser Modell erlaubt uns für jeden beliebigen Wert des Prädiktors eine Post-Verteilung (von $\mu$) zu berechnen. Hier am Beispiel von m_kung_post, s. Abbildung 9.16.

Abbildung 9.16: Für jeden beliebigen Prädiktorwert kann man eine Post-Verteilung bekommen. A: Regressionsmodell mit einigen ausgewählten Gewichtswerten. Es ist jeweils die Wahrscheinlichkeitsverteilung für den vorhergesagten Y-Wert dargestellt (hier sind die Verteilungen zu groß dargestellt zur besseren Sichtbarkeit). B: Für jeden beliebigen Gewichtswert (Y) bekommt man eine (auf den jeweiligen X-Wert bedingten) Post-Verteilung.

9.5.2 Visualisierung

Was ist wohl die Wahrscheinlichkeit der Körpergröße bei einem bestimmten Gewicht? Angenommen wir wissen, dass das Gewicht bei, sagen wir 45 kg liegt. Welche Körpergröße ist (im Schnitt) zu erwarten? Wie unsicher sind wir uns über diesen Mittelwert? Etwas formaler ausgedrückt: $\mu |\text{weight}=45$

45 kg entspricht genau dem Mittelwert von weight. Geht man von zentrierten Prädiktorwerten aus, gilt in dem Fall weight_c = 0. Erstellen wir uns dazu eine Tabelle, Und plotten diese, s. Abbildung 9.17.

mu_at_45 <-
  m_kung_gewicht_c_post %>% 
  mutate(mu_at_45 = `(Intercept)`)

mu_at_45 %>% 
  ggplot(aes(x = mu_at_45)) +
  geom_density()

Abbildung 9.17: Post-Verteilung der Größe (laut unserem Modell) bei einem Gewicht von 45kg

Analog können wir fragen, wie groß wohl eine Person mit 50 kg im Mittelwert sein wird und wie (un)gewiss wir uns über diesen Mittelwert sind. 50 kg, das sind 5 über dem Mittelwert, in zentrierten Einheiten ausgedrückt also weight_c = 5. Auch dazu erstellen wir uns eine Tabelle, s. Tabelle 9.6. Die Verteilung der mittleren Größe bei einem Gewicht von 50kg ist weiter “rechts” (Richtung höhere Größe) lokalisiert, s. Abbildung 9.18. Dazu addieren wir zum Wert des Achsenabschnitts (intercept) das Fünffache des Regressionsgewichts, ${\beta }_1$ (weight_c): mu_at_50 = (Intercept)m + 5 * weight_c. Das Diagramm erhält man mit ggplot(mu_at_50, aes(x = mu_at_50)) + geom_density().

mu_at_50 <-
  mu_at_45 %>% 
  mutate(mu_at_50 = `(Intercept)` + 5 * weight_c)

head(mu_at_50)

Tabelle 9.6: Die Verteilung von mu bedingt auf ein Gewicht von 50kg.

ABCDEFGHIJ0123456789

(Intercept) <dbl>	weight_c <dbl>	sigma <dbl>	mu_at_45 <dbl>	mu_at_40 <dbl>	mu_at_50 <dbl>	mu_at_55 <dbl>
155	0.90	5.4	155	150	159	164
155	0.91	5.0	155	150	159	164
155	0.92	5.2	155	150	159	164
155	0.90	5.0	155	150	159	164
155	0.89	5.2	155	150	159	164

Next

12

Previous

1-5 of 6 rows

Abbildung 9.18: Post-Verteilung der mittleren Größe (laut unserem Modell) bedingt auf ein Gewicht von 50 kg

9.5.3 Lagemaße und Streuungen

Befragen wir die bedingte Post-Verteilung. Eine erste Frage zielt nach den typischen deskriptiven Statistiken, also nach Lage und Streuung der Verteilung der Körpergröße.

Was ist das 90% ETI für $\mu |w=50$? Man erhält es mit dem Befehl mu_at_50 %>% eti(ci = .9)

#|echo: false
mu_at_50 %>% 
  eti(ci = .9)

ABCDEFGHIJ0123456789

Parameter <chr>	CI <dbl>	CI_low <dbl>	CI_high <dbl>
(Intercept)	0.9	154.19	155.09
weight_c	0.9	0.84	0.98
sigma	0.9	4.83	5.46
mu_at_45	0.9	154.19	155.09
mu_at_40	0.9	149.54	150.68

Next

12

Previous

1-5 of 7 rows

Die mittlere Größe – gegeben $w=50$ – liegt mit 90% Wahrscheinlichkeit zwischen den beiden Werten (ca.) 159 cm und 160 cm.

Welche mittlere Größe wird mit 95% Wahrscheinlichkeit nicht überschritten, wenn die Person 45kg wiegt? Dazu berechnen wir das gefragte Quantil (also bei 95%).

mu_at_45 %>% 
  summarise(q_95 = quantile(mu_at_45, prob = .95))

ABCDEFGHIJ0123456789

q_95 <dbl>
155

1 row

9.6 Fazit

9.6.1 Ausstieg

Beispiel 9.2 (Fassen Sie das Wesentliche zusammen!) Schreiben Sie 5-10 Sätze zum Wesentlichen Stoff dieses Kapitels und reichen Sie bei der von Lehrkraft vorgegebenen Stelle ein! $◻$

9.6.2 Vertiefung

McElreath (2020) bietet eine tiefere Darstellung von linearen Modellen auf Basis der Bayes-Statistik, insbesondere Kapitel 4 daraus vertieft die Themen dieses Kapitels. Kurz (2021) greift die R-Inhalte von McElreath (2020) auf und setzt sie mit Tidyverse-Methoden um; ein interessanter Blickwinkel, wenn man tiefer in die R-Umsetzung einsteigen möchte. Gelman et al. (2021) bieten ebenfalls viele erhellende Einblicke in das Thema Regressionsanalyse, sowohl aus einer frequentistischen als auch aus einer Bayes-Perspektive.

9.7 Aufgaben

9.7.1 Papier-und-Bleistift-Aufgaben

1. Bayes-Ziel1
2. Bayesmod-bestimmen01
3. mtcars-post2a
4. Bed-Post-Wskt1
5. mtcars-post3a
6. regression1a
7. regression1b
8. Regression2
9. Priorwahl1
10. Bayesmod-bestimmen02
11. Aussagen-einfache-Regr
12. Likelihood-identifizieren
13. Priorwahl2
14. Likelihood2
15. interpret-koeff
16. bed-post-wskt1

9.7.2 Computer-Aufgaben

1. Post-befragen1
2. penguins-stan-01

9.8 —

Gelman, A., Hill, J., & Vehtari, A. (2021). Regression and Other Stories. Cambridge University Press.

Kurz, S. (2021). Statistical Rethinking with Brms, Ggplot2, and the Tidyverse: Second Edition. https://bookdown.org/content/4857/

Makowski, D., Ben-Shachar, M. S., Chen, S. H. A., & Lüdecke, D. (2019). Indices of Effect Existence and Significance in the Bayesian Framework. Frontiers in Psychology, 10. https://www.frontiersin.org/article/10.3389/fpsyg.2019.02767

McElreath, R. (2020). Statistical Rethinking: A Bayesian Course with Examples in R and Stan (2. Aufl.). Taylor and Francis, CRC Press.

---

1. Da es viele Funktionen sind, bietet es sich an mit Strg-F auf der Webseite nach Ihrem Lieblingsbefehl zu suchen.

2. Datenquelle, McElreath (2020).

3. Wer ist hier für die Namensgebung zuständig? Besoffen oder was?

4. oder zumindest besser sichergestellt

5. In manchen Lehrbüchern wird ${\beta }_0$ auch als $\alpha$ bezeichnet.

6. 1e6

7. Im Standard beschert uns stan_glm() 4000 Stichproben.

8. $\mu$