4 Rechnen mit Wahrscheinlichkeiten

4.1 Lernsteuerung

4.1.1 Position im Modulverlauf

Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.

4.1.2 Überblick

Dieses Kapitel stellt uns einige grundlegenden Rechengesetze für Wahrscheinlichkeiten vor: Wann man die Wahrscheinlichkeiten zweier Ereignisse addiert oder multipliziert. Außerdem lernen wir den Begriff der Unabhängkeit kennen.

4.1.3 Lernziele

Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.

Sie können …

die Grundbegriffe der Wahrscheinlichkeitsrechnung erläuternd definieren
typische Relationen (Operationen) von Ereignissen anhand von Beispielen veranschaulichen
mit Wahrscheinlichkeiten rechnen

4.1.4 Begleitliteratur

Lesen Sie zur Begleitung dieses Kapitels Bourier (2011), Kap. 2-4.

4.1.5 Prüfungsrelevanter Stoff

Der Stoff dieses Kapitels deckt sich (weitgehend) mit Bourier (2011), Kap. 2-4. Weitere Übungsaufgaben finden Sie im dazugehörigen Übungsbuch, Bourier (2022).

Hinweis

In Ihrer Hochschul-Bibliothek kann das Buch als Ebook verfügbar sein. Prüfen Sie, ob Ihr Dozent Ihnen weitere Hilfen im geschützten Bereich (Moodle) eingestellt hat. $◻$

4.2 Überblick

Die Rechenregeln der Wahrscheinlichkeit erlauben es, für bestimmte Situationen eine Wahrscheinlichkeit hzu berechnen. Das hört sich vielleicht wild an, ist aber oft ganz einfach.

Beispiel 4.1 (Wahrscheinlichkeit für eine gerade Zahl beim Würfelwurf) Ein (normaler) Würfel wird geworfen. Was ist die Wahrscheinlichkeit für eine gerade Zahl, also für das Ereignis $A = {2, 4, 6}$ ? Diese Wahrscheinlichkeit beträgt $P r (gerade Zahl) = 1 / 6 + 1 / 6 + 1 / 6 = 3 / 6 = 1 / 2$ . $◻$

Beispiel 4.2 (Gezinkter Würfel) Ein gezinkter Würfel hat eine erhöhte Wahrscheinlichkeit für das Ereignis $A =$ “6 liegt oben”, und zwar gelte $P r (A) = 1 / 3$ . Was ist die Wahrscheinlichkeit, keine 6 zu würfeln? $◻$ ¹

4.3 Additionssatz

Der Additionssatz wird verwendet, wenn wir an der Wahrscheinlichkeit interessiert sind, dass mindestens eines der Ereignisse A und B eintritt. “Mindestens eines der Ereignisse A und” schreibt man $A \cup B$ und sagt “A vereinigt B”.

4.3.1 Addition disjunkter Ereignisse

Gegeben sei $Ω = 1, 2, 3, 4, 5, 6$ beim normalen Würfelwurf. Als Sinnbild: $1 2 3 4 5 6$ . Gesucht sei die Wahrscheinlichkeit des Ereignis $A = {1, 2}$ , das also eine 1 oder
eine 2 geworfen wird. Man beachte, dass die beiden Ergebnisse disjunkt sind, s. Abbildung 3.6: Wenn man eine 1 wirft, hat man keine 2 geworfen.

$1 2 3 4 5 6$

Die Wahrscheinlichkeit für $A$ ist die Summe der Wahrscheinlichkeiten der einzelnen Ereignisse (1 und 2):

$P r (1 \cup 2) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6}$

Definition 4.1 (Additionssatz für disjunkte Ereignisse) Die Wahrscheinlichkeit, dass mindestens eines der beiden Ereignisse eintritt, ist die Summe der Einzelwahrscheinlichkeiten, s. Theorem 4.1.

Theorem 4.1 (Additionssatz für disjunkte Ereignisse) $P r (A \cup B) = P (A) + P (B) ◻$

Beispiel 4.3 Was ist die Wahrscheinlichkeit, an einem Samstag oder Sonntag geboren zu sein? Unter der (vereinfachten) Annahme, dass alle Jahre zu gleichen Teilen aus allen Wochentagen bestehen und dass an allen Tagen gleich viele Babies geworden werden², ist die Antwort $P r (A) = 1 / 7 + 1 / 7 = 2 / 7$ . $◻$

4.3.2 Addition allgemeiner Ereignisse

Unter allgemeinen Ereignissen verstehen wir hier sowohl disjunkte als auch nicht disjunkte. Bei der Addition der Wahrscheinlichkeiten für $A$ und $B$ wird der Schnitt $A \cap B$ (der Überlappungsbereich) doppelt erfasst – sofern sie nicht disjunkt sind, aber wenn sie disjunkt sind, so ist der Schnitt gleich Null und wir machen auch dann nichts falsch. Der Überlappungsbereich muss daher noch abgezogen werden, s. Abbildung 4.1.

Definition 4.2 (Allgemeiner Additionssatz) Die Wahrscheinlichkeit, dass mindestens eines der beiden Ereignisse $A$ und $B$ eintritt, ist gleich der Summe ihrer Wahrscheinlichkeiten minus ihrer gemeinsamen Wahrscheinlichkeit, s. Theorem 4.2 und Abbildung 4.1. $◻$

Theorem 4.2 (Allgemeiner Additionssatz) $P r (A \cup B) = P (A) + P (B) - P (A \cap B) ◻$

Abbildung 4.1: Der allgemeine Additionssatz gibt die Wahrscheinlichkeit, dass mindestens eines der beiden Ereignisse eintritt.

Beispiel 4.4 (Lernen und Klausur bestehen) In einem Psychologie-Studiengang sind die Studis verdonnert, zwei Statistik-Module ( $S 1, S 2$ ) zu belegen. Die meisten bestehen ( $B$ ), einige leider nicht ( $N$ ), s. Tabelle 4.1.

Ereignis $S_{1} B$ sei “Klausur Statistik 1 bestanden” Ereignis $S_{2} B$ ist analog für “Klausur Statistik 2”.

Wir suchen die Wahrscheinlichkeit des Ereignisses A, d.h. mindestens eine der beiden Klausuren zu bestehen: $P r (A) = P r (S_{1} B \cup S_{2} B)$ .

Tabelle 4.1: Daten von 100 Studis; L: Lerner, B: Bestanden, N: Negation/Nicht

.	S1_B	S1_NB	Summe
S2_B	85	9	94
S2_NB	5	1	6
Summe	90	10	100

\begin{aligned} P r (A) & = P r (S_{1} B \cup S_{2} B) \\ = P r (S 1_{B}) + P r (S_{2} B) - P r (S_{1} B \cap S_{2} B) \\ = (90 + 94 - 85) / 100 = 99 / 100 \end{aligned}

Die Wahrscheinlichkeit, mindestens eine der beiden Klausuren zu bestehen liegt bei 99%.

Übungsaufgabe 4.1 (Peer Instruction: Keine Klausur bestanden) Wie hoch ist die Wahrscheinlichkeit, keine der beiden Klausuren zu bestehen?

1%
5%
6%
9%
10%
16% $◻$

4.4 Bedingte Wahrscheinlichkeit

4.4.1 Illustration zur bedingten Wahrscheinlichkeit

Definition 4.3 (Bedingte Wahrscheinlichkeit) Die bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass $A$ eintritt, gegeben dass $B$ schon eingetreten ist. $◻$

Man schreibt: $P r (A | B) .$ Lies: “A gegeben B” oder “A wenn B”.

Übungsaufgabe 4.2 Schauen Sie sich mal diese Animation von Victor Powell an zu bedingten Wahrscheinlichkeiten an. Sehenswert.

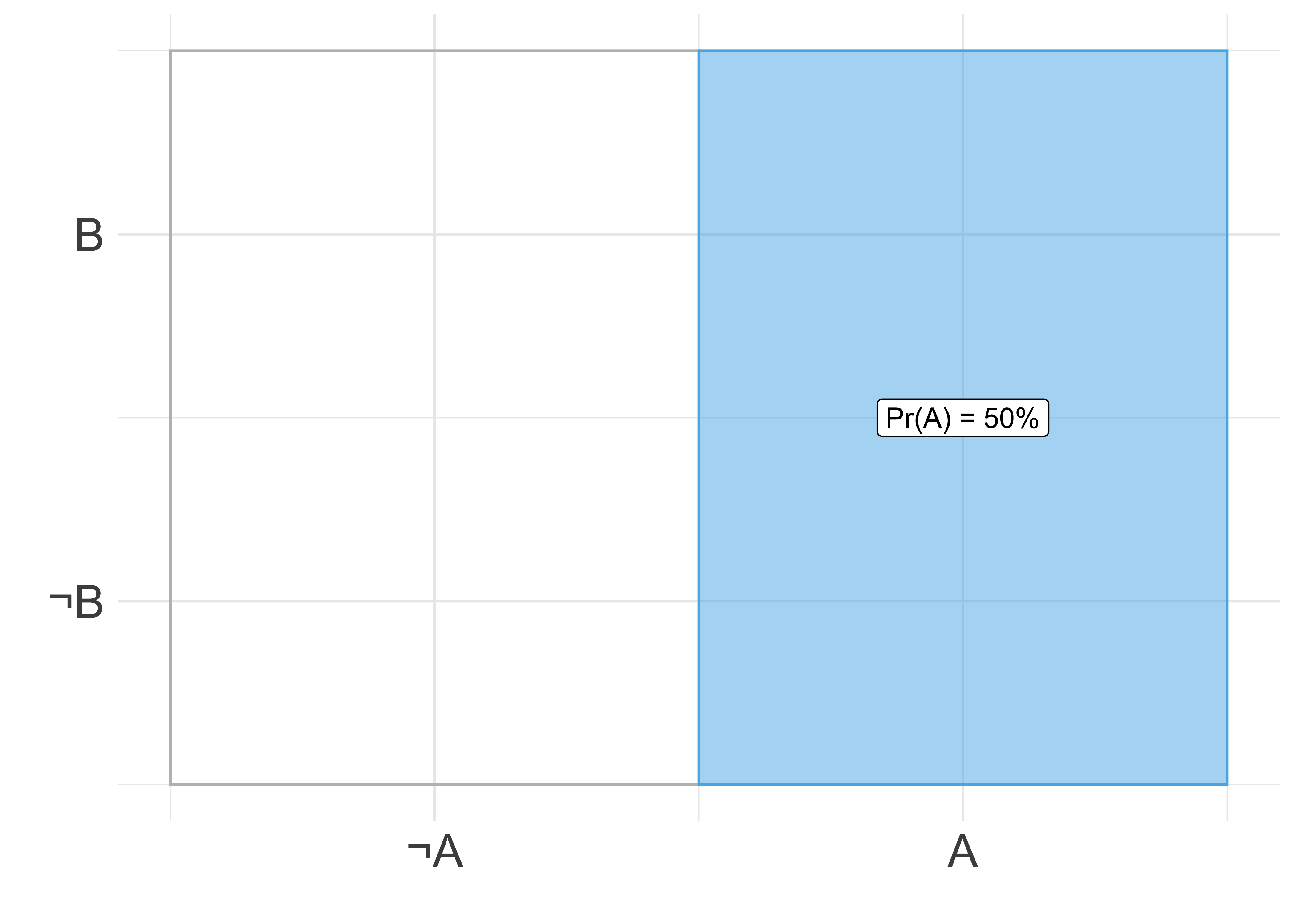
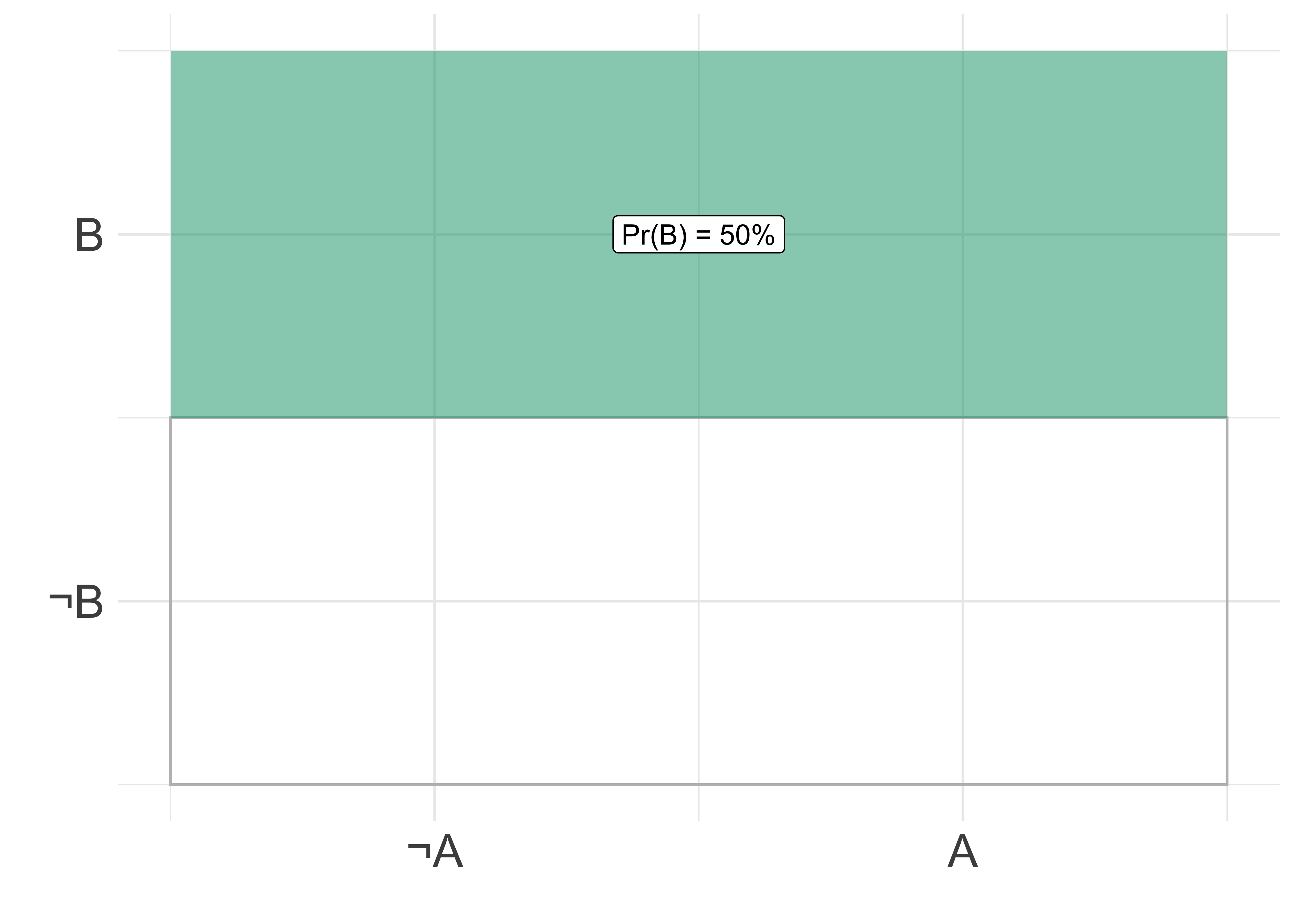
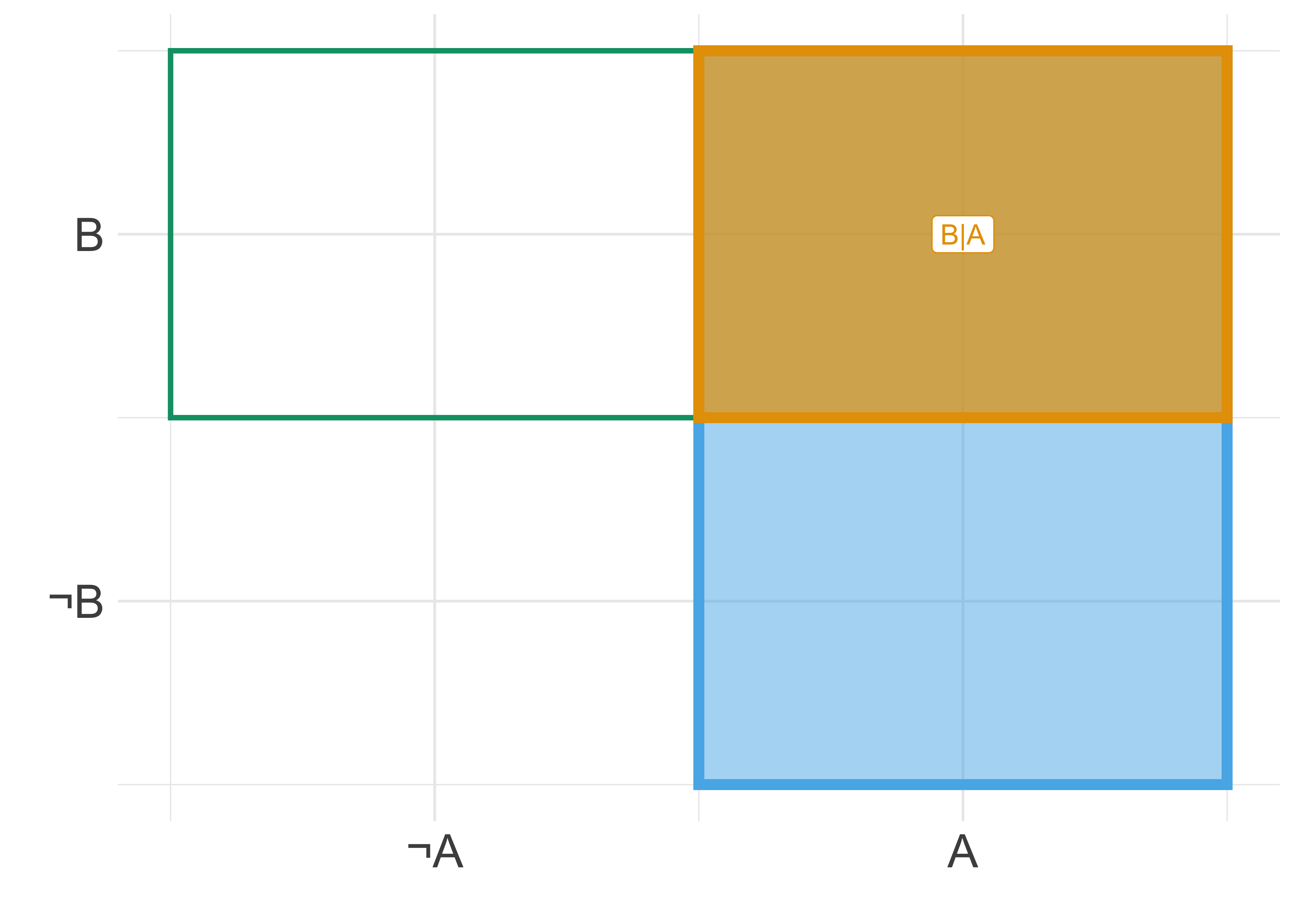
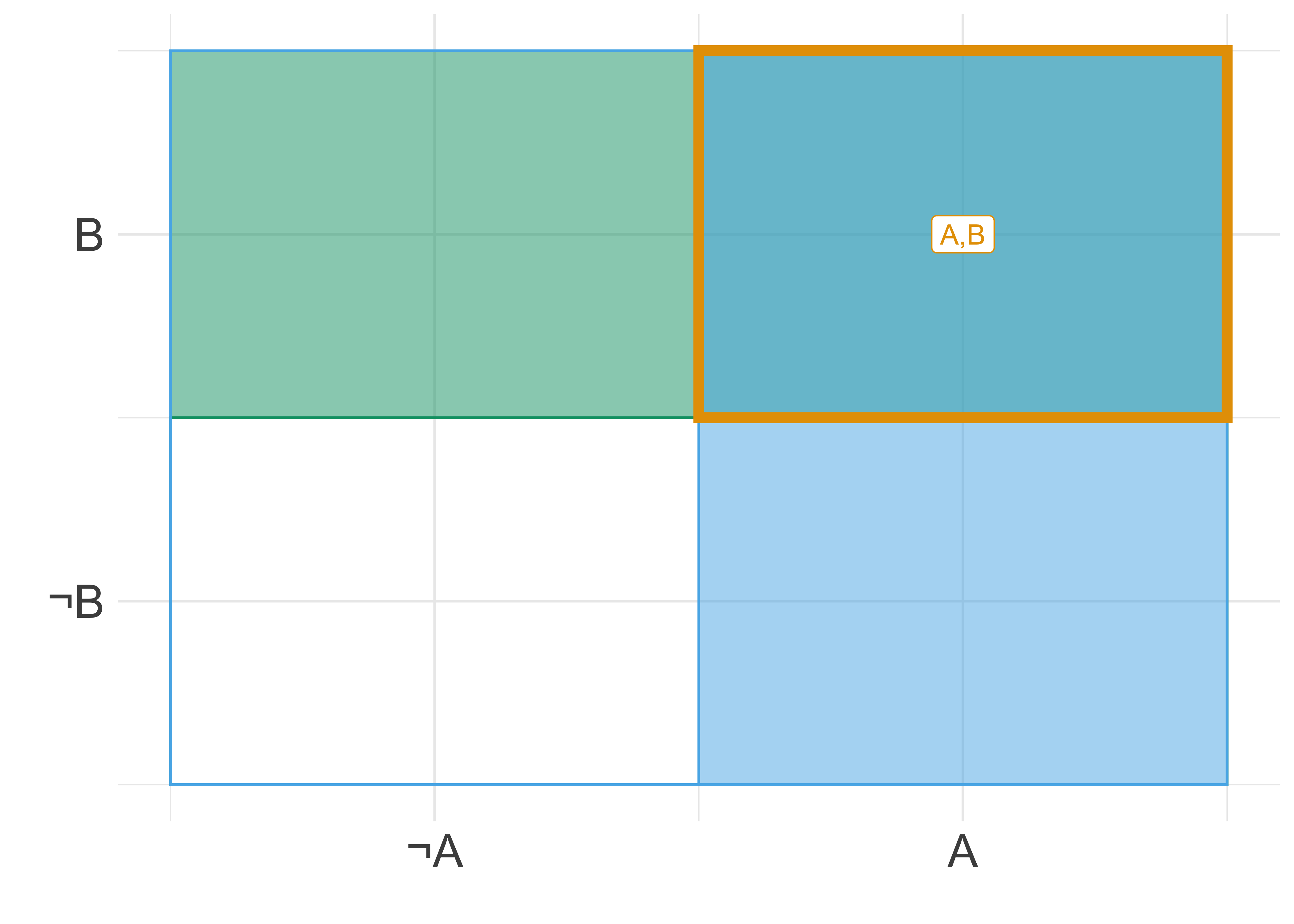
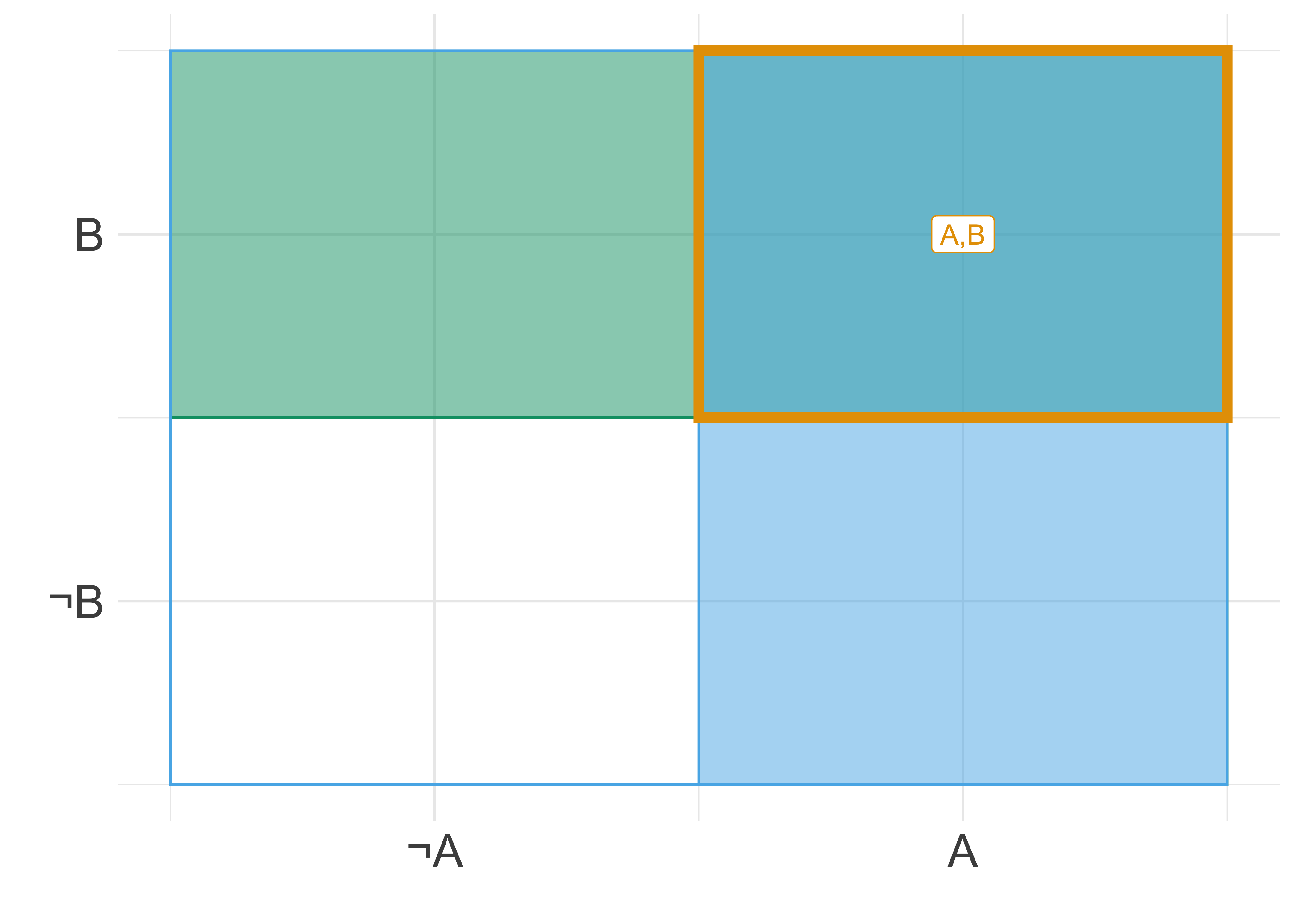
Abbildung 4.2 illustriert unbedingte Wahrscheinlichkeit, $P r (A), P r (B)$ , gemeinsame Wahrscheinlichkeit $P r (A \cap B)$ , und bedingte Wahrscheinlichkeit, $P r (A | B)$ .

(a) Unbedingte Wahrscheinlichkeit für Ereignis A: 50%=1/2

Beispiel 4.5 (Bedingte Wahrscheinlichkeit) Sei $A$ “Schönes Wetter” und $B$ “Klausur steht an”. Dann meint $P r (A | B)$ die Wahrscheinlichkeit, dass das Wetter schön ist, wenn gerade eine Klausur ansteht. $◻$

Beispiel 4.6 (Von Päpsten und Männern) Man(n) beachte, dass die Wahrscheinlichkeit, Papst $P$ zu sein, wenn man Mann $M$ ist etwas anderes ist, als die Wahrscheinlichkeit, Mann zu sein, wenn man Papst ist: $P r (P | M) \neq P r (M | P)$ . Das hört sich erst verwirrend an, aber wenn man darüber nachdenkt, wird es plausibel. $◻$

Beispiel 4.7 Gustav Groß-Gütz verkauft eine Tinktur³, die schlau machen soll, “Gützis Gehirn Grütze”.⁴ Gustav trinkt die Grütze und sagt schlaue Dinge. Was schließen wir daraus? Sei $H$ (wie Hypothese) “Gützis Grütze macht schlau”; sei $D$ (wie Daten) die Beobachtung, dass Gustav schlaue Dinge gesagt hat. Ohne exakte Zahlen zu suchen, wie hoch ist wohl $P r (D | H)$ ? In Worten: “Wie wahrscheinlich ist es, schlaue Dinge gesagt zu haben, wenn die Grütze wirklich schlau macht?”. Vermutlich ist diese Wahrscheinlichkeit sehr hoch. Aber wie hoch ist wohl $P r (H | D)$ ? In Worten: “Wie wahrscheinlich ist es, dass die Grütze wirklich schlau macht, gegeben, dass wir gesehen hat, dass jemand etwas schlaues gesagt hat, nachdem er besagte Grütze getrunken hat?” Skeptische Geister werden der Meinung sein, $P r (H | D)$ ist gering. Das Beispiel zeigt u.a. $P r (H | D) \neq P r (D | H) . ◻$

4.4.2 Bedingte Wahrscheinlichkeit als Filtern einer Tabelle

Betrachten wir Tabelle 4.2. Dort sind sind vier Tage aufgelistet, mit jeweils Regen (oder kein Regen) bzw. an denen es kalt ist (oder nicht). Filtern wir z.B. die Tabelle so, dass nur kalte Tage übrig bleiben, dann gibt der Anteil der Zeilen, die “Regen” anzeigen, die bedingte Wahrscheinlichkeit $P r (Regen | kalt)$ an.

Tabelle 4.2: Die Tabelle zeigt vier Tage, an denen es jeweils kalt ist (oder nicht) bzw. regnet (oder nicht). Die bedingte Wahrscheinlichkeit

P r (Regen | kalt)

entspricht dem Anteil der Zeilen mit Regen, wenn für ‘kalt’ ein Filter in der Tabelle gesetzt ist.

Show entries

Search:

	id	kalt	Regen
1	1	nein	nein
2	2	nein	ja
3	3	ja	nein
4	4	ja	ja

Showing 1 to 4 of 4 entries

Previous1Next

Also: Das Berechnen einer bedingten Wahrscheinlichkeit, $P r (A | B)$ , ist vergleichbar zum Filtern einer Tabelle, s. Tabelle 4.3.

Tabelle 4.3: Eine bedingte Wahrscheinlichkeit kann man als gefilterte Tabelle verstehen

id	kalt	Regen
1	0	0
2	0	1
3	1	0
4	1	1
SUMME	2	2

Es ergeben sich folgende Wahrscheinlichkeiten:

$P r (A) = 2 / 4; P r (B) = 2 / 4; P r (A \cap B) = 1 / 4; P r (A | B) = 1 / 2$

Die Wahrscheinlichkeit für $A$ , wenn $B$ schon eingetreten ist, berechnet sich so, s. Theorem 4.3 und Abbildung 4.2 (c).

Theorem 4.3 (Bedingte Wahrscheinlichkeit) $P r (A | B) = \frac{P r (A \cap B)}{P r (B)}$

Außerdem gilt analog

$P r (B | A) = \frac{P r (B \cap A)}{P r (A)} ◻$

Beispiel 4.8 (Lernen und Klausur bestehen) Sie bereiten sich gerade auf die Klausur bei Prof. Süß vor. Das heißt: Sie überlegen, ob Sie sich auf die Klausur vorbereiten sollten. Vielleicht lohnt es sich ja gar nicht? Vielleicht ist die Wahrscheinlichkeit zu bestehen, wenn man nicht gelernt hat, sehr groß? Aber da Sie nun mal auf Fakten stehen, haben Sie sich nach einiger Recherche folgende Zahlen besorgen können, s. Tabelle 4.4. In der Tabelle sind die Daten von 100 Studis ausgewiesen. Ein Teil hat sich vorbereitet, ordentlich gelernt, nenen wir sie die “Lerner”. Ein anderer Teil hat nicht gelernt, $N L$ bzw. $\neg L$ . Ein Teil hat bestanden, $B$ , ein Teil nicht $N B$ oder $\neg B$ .

Wir suchen die Wahrscheinlichkeit, zu bestehen, wenn man nicht gelernt hat: $P r (B | \neg L)$ .

Tabelle 4.4: Daten von 100 Studis; L: Lerner, B: Bestanden, N: Negation/Nicht

.	L	NL	Summe
B	80	1	81
NB	5	14	19
Summe	85	15	100

\begin{aligned} P r (B | \neg L) & = \frac{P r (B \cap \neg L)}{P r (\neg L)} \\ = \frac{1 / 100}{15 / 100} = 1 / 15 \end{aligned}

Die Wahrscheinlichkeit, zu bestehen, wenn man nicht gelernt hat, liegt bei 1 von 15, also ca. 7%.⁵ $◻$

Beispiel 4.9 (Kalt und Regen) Die Wahrscheinlichkeit, dass es kalt ist, wenn es regnet, ist gleich der Wahrscheinlichkeit, dass es gleichzeitig kalt ist und regnet, geteilt durch die Wahrscheinlichkeit, dass es regnet. $◻$

4.5 Stochastische (Un-)Abhängigkeit

4.5.1 Unabhängigkeit

Stochastische Unabhängigkeit ist ein Spezialfall von Abhängigkeit: Es gibt sehr viele Ausprägungen für Abhängigkeit, aber nur eine für Unabhängigkeit. Können wir Unabhängigkeit nachweisen, haben wir also eine starke Aussage getätigt.

Definition 4.4 (Stochastische Unabhängigkeit) Zwei Ereignisse sind (stochastisch) unabhängig voneinander, wenn die Wahrscheinlichkeit von $A$ nicht davon abhängt, ob $B$ der Fall ist, s. Theorem 4.4. Anders gesagt:⁶

Theorem 4.4 (Stochastische Unabhängigkeit) $P r (A) = P r (A | B) = P r (A | \neg B) ◻$

In Worten: Wenn die Wahrscheinlichkeit von A sich nicht ändert, wenn B eingetreten ist, so ist A von B (stochastisch) unabhängig.

Die Unabhängigkeit von $A$ und $B$ wird manchmal so in Kurzschreibweise ausgedrückt: $⊥ ⊥ (A, B) ◻$ .

Theorem 4.5 (Stochastische Unabhängigkeit 2) Setzt man Theorem 4.3 in Theorem 4.4 (linke Seite) ein, so folgt⁷

$P r (A \cap B) = P r (A) \cdot P r (B) . ◻$

In Worten: Die Wahrscheinlichkeit, dass A und B beide der Fall sind, ist gleich dem Produkt ihrer jeweiligen Wahrscheinlichkeiten.

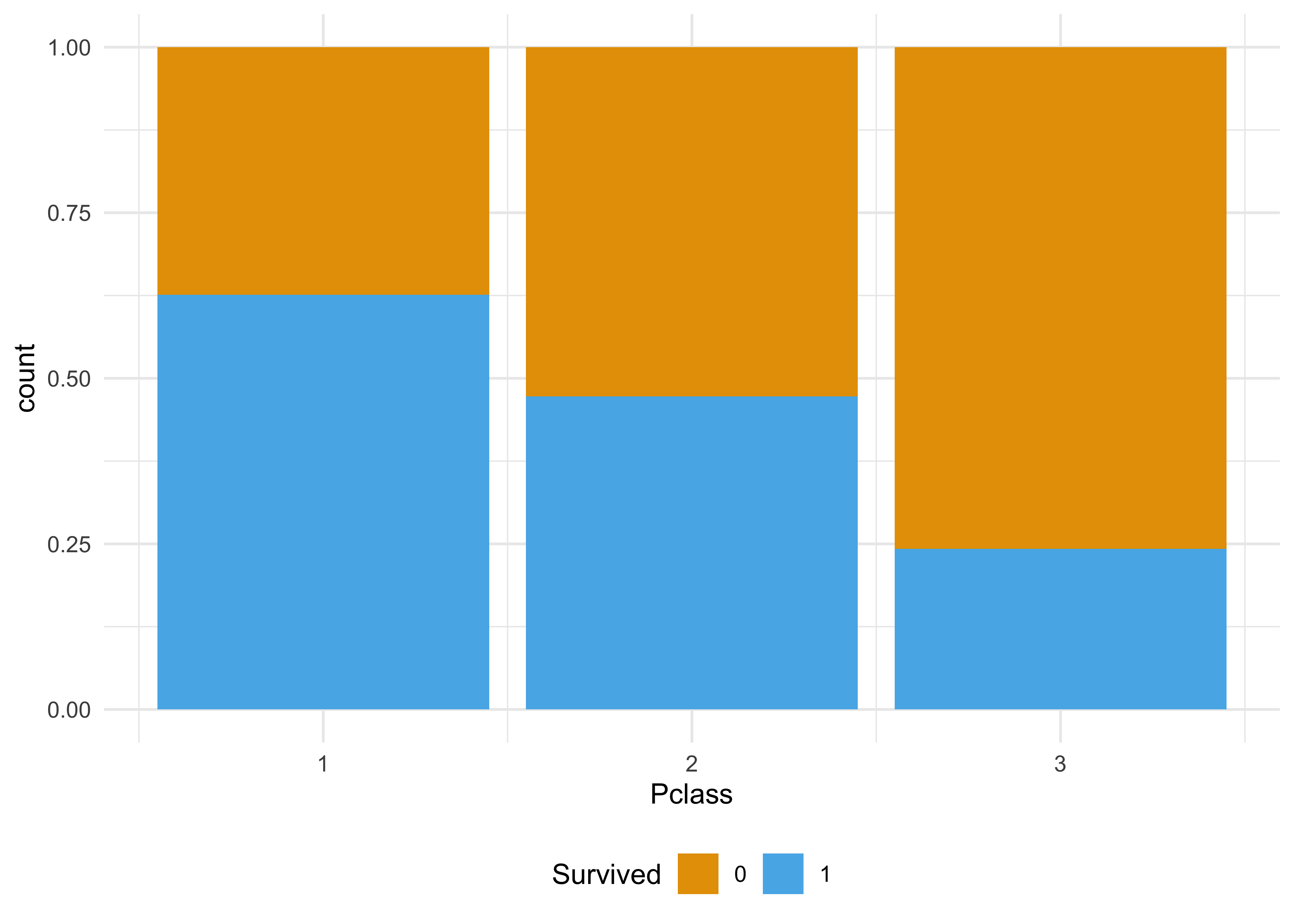
Beispiel 4.10 (Augenfarbe und Statistikliebe) Ich vermute, dass die Ereignisse $A$ , “Augenfarbe ist blau”, und $B$ , “Ich liebe Statistik”, voneinander unabhängig sind. $◻$ ⁸

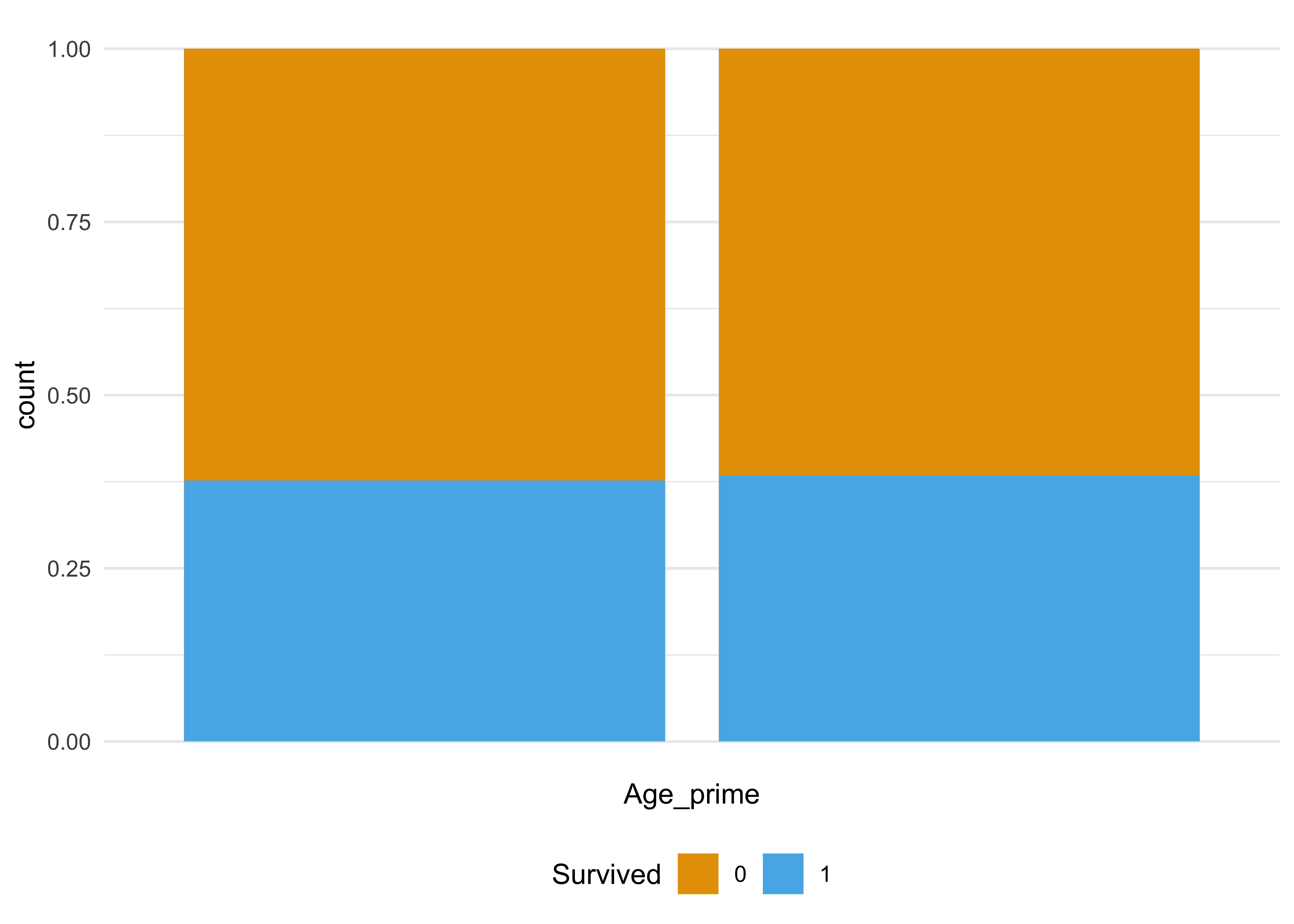
Beispiel 4.11 (Überleben auf der Titanic) S. Abbildung 4.3, links: Überleben (Ü) auf der Titanic ist offenbar abhängig von der Passagierklasse ( $K_{1}, K_{2}, K_{3}$ ). In Abbildung 4.3, links gilt also $P r (Ü | K_{1}) \neq P r (Ü | K_{2}) \neq P r (Ü | K_{3}) \neq P r (Ü)$ .

Auf der anderen Seite: Das Ereignis Überleben (Ü) auf der Titanic ist unabhängig vom Ereignis Alter ist eine Primzahl (P), s. Abbildung 4.3, rechts. Also: $P r (Ü | P) = P r (Ü | \neg P) = P r (Ü)$ , vgl. Tabelle 4.5.

Tabelle 4.5: Kontingenztablle (Häufigkeiten) für ‘Überleben auf der Titanic’ und ‘Alter ist Primzahl’. Wie man sieht, gibt es keine stochastische Abhängigkeit.

Age_prime	n	prop
0
non-prime	96	0.17
prime	453	0.83
1
non-prime	58	0.17
prime	282	0.83

(a) Überleben und Passagierklasse sind abhängig

4.5.2 Stochastische Abhängigkeit

Liegt keine Unabhängigkeit vor, so spricht man von (stochastistischer) Abhängigkeit, s. Theorem 4.6. In diesem Fall verändert sich unser Wissen über die Wahrscheinlichkeit von $A$ , wenn wir wissen, dass $B$ eingetroffen ist, s. Theorem 4.6.

Theorem 4.6 (Stochastische Abhängigkeit) $P r (A | B) \neq P r (A) \neq P r (A | \neg B) ◻$

In Worten: Ändert sich die Wahrscheinlichkeit von A, wenn B der Fall ist, so sind A und B voneinander (stochastich) abhängig.

Theorem 4.6 gilt natürlich in dieser Form für alle anderen Variablen ebenso, s. z.B. Theorem 4.7. $◻$

Theorem 4.7 (Stochastische Abhängigkeit 2) $P r (B | A) \neq P r (B) \neq P r (B | \neg A) ◻$

Beispiel 4.12 Die Ereignisse “Lernen” und “Klausur bestehen” seien voneinander abhängig. Unsere Einschätzung zur Wahrscheinlichkeit von K ändert sich, wenn wir wissen, dass L vorliegt. Genauso wird sich unsere Einschätzung zur Wahrscheinlichkeit von K ändern, wenn wir wissen, dass L nicht vorliegt. $◻$

Beispiel 4.13 (Zusammenhang von Covidsterblichkeit und Impfquote) Sind die Ereignisse Tod durch Covid bzw. Impfquote ( $A$ ) und Land⁹ ( $B$ ) voneinander abhängig (s. Abbildung 4.4)?

(a) Impfquote und Land sind voneinander abhängig

Ja, die beiden Ereignisse sind abhängig, da in beiden Diagrammen gilt: $P r (A | B) \neq P r (A) \neq P r (A | \neg B)$ . $◻$ ¹⁰

4.5.3 Unabhängigkeit ist symmetrisch

Stochastische Unabhängigkeit ist symmetrisch: Wenn $A$ unabhängig zu $B$ ist auch $B$ unabhängig zu $A$ , s. Theorem 4.8.

Theorem 4.8 (Symmetrie der Unabhängigkeit) $P r (A | B) = P r (A) \leftrightarrow P r (B | A) = P r (B)$

Man beachte, dass stochastische Unabhängigkeit und kausale Unabhängigkeit unterschiedliche Dinge sind (Henze, 2019): Stochastische Unabhängigkeit impliziert nicht kausale Unabhängigkeit. $◻$

Übungsaufgabe 4.3 (Peer Instruction: Welche Aussagen über stochastische Unabhängigkeit ist korrekt?)

Wenn X und Y unabhängig sind, dann hat X keinen Einfluss auf Y im Alltag.
Zwei Ereignisse A und B sind unabhängig, wenn sie sich nicht überschneiden.
Wenn X und Y unkorreliert sind, dann sind sie unabhängig.
Wenn X und Y abhängig sind, dann können sie nicht gleichzeitig positive Korrelation haben.
Wenn X und Y unabhängig sind, sind sie auch unkorreliert.

4.6 Multiplikationssatz

Gegeben seien die Ereignisse $A$ und $B$ . Der Multiplikationssatz wird verwendet, wenn wir an der Wahrscheinlichkeit interessiert sind, dass beide Ereignisse $A$ und $B$ der Fall sind; Abbildung 4.2 (d) verdeutlicht dies für zwei unabhängige Ereignisse. Man schreibt “A und B” als $A \cap B$ (lies “A geschnitten B” oder “A und B”) oder kurz $A B$ , um anzuzeigen, dass sowohl $A$ als auch $B$ eingetreten sind.

Beide Ereignisse A und B sind eingetreten

Beispiel 4.14 (Wieder kalt und Regen) Es ist eine Sache, zu fragen, wie wahrscheinlich ist ist, dass es kalt ist (bei Kälte), wenn es regnet (bei Regen): $P r (K | R)$ . Anders gesagt: “Wie groß ist die Wahrscheinlichkeit für Kälte, gegeben dass es regnet?” Eine andere Sache ist es, nach der Wahrscheinlichkeit zu fragen, dass es gleichzeitig kalt ist und regnet, dass also beide Ereignisse (kalt und Regen) eintreten: $P r (K \cap R), P r (K R)$ . $◻$

4.6.1 Gemeinsame Wahrscheinlichkeit unabhängiger Ereignisse

Beispiel 4.15 Wir führen das Zufallsexperiment “Wurf einer fairen Münze” zwei Mal aus (Abbildung 4.5). Wie groß ist die Wahrscheinlichkeit, 2 Mal Kopf zu werfen? Dabei vereinbaren wir, dass “Kopf” als “Treffer” zählt (und “Zahl” als “Niete”). $◻$

Abbildung 4.5: Wir werfen zwei faire Münzen: Zweifach wiederholtes Zufallsexperiment

Abbildung 4.5 zeigt ein Baumdiagramm. Jeder Kasten (Knoten) zeigt ein Ergebnis des Zufallexperiments. Die Pfeile (Kanten) symbolisieren die Abfolge des Experiments: Vom “Start” (schwarzer Kreis) führen zwei mögliche Ergebniss ab, jeweils mit Wahrscheinlichkeit 1/2. Die untersten Knoten nennt man auch Blätter (Endknoten), sie zeigen das Endresultat des (in diesem Fall) zweifachen Münzwurfs. Der Weg vom Start zu einem bestimmten Blatt nennt man Pfad. Die Anzahl der Pfade entspricht der Anzahl der Blätter. In diesen Diagramm gibt es vier Pfade (und Blätter).

Den Wurf der ersten Münze nennen wir in gewohnter Manier $A$ ; den Wurf der zweiten Münze $B$ .

Die Wahrscheinlichkeiten der resultierenden Ereignisse finden sich in Tabelle 4.6.

Tabelle 4.6: Wahrscheinlichkeiten der Ereignisse im zweimaligen Münzwurf

Ereignis	Pr
0K	1/2 * 1/2 = 1/4
1K	1/4 + 1/4 = 1/2
2K	1/2 * 1/2 = 1/4

Sei $K_{1}$ das Ereignis, mit der 1. Münze Kopf zu werfen; sei $K_{2}$ das Ereignis, mit der 2. Münze Kopf zu werfen.

Wir suchen $P r (K_{1} \cap K_{2})$ . Aufgrund der stochastischen Unabhängigkeit der beiden Ereignisse gilt: $P r (K_{1} \cap K_{2}) = P r (K_{1}) \cdot P r (K_{2})$ .

Code

Pr_K1K2 <- 1/2 * 1/2
Pr_K1K2
## [1] 0.25

Definition 4.5 (Multiplikationssatz für unabhängige Ereignisse) Die Wahrscheinlichkeit, dass zwei (oder mehr) unabhängige Ereignisse $A$ und $B$ gemeinsam eintreten, ist gleich dem Produkt ihrer jeweiligen Wahrscheinlichkeiten, s. Theorem 4.9. $◻$

Theorem 4.9 (Multiplikationssatz für unabhängige Ereignisse) $P r (A \cap B) = P r (A) \cdot P r (B)$

Man beachte, dass es egal ist, ob $A$ gemeinsam mit $B$ oder $B$ gemeinsam mit $A$ eintreten: $P r (A \cap B) = P r (B \cap A)$ . Man spricht in diesem Zusammenhang von der Symmetrie der Multiplikation. $◻$

Mit dieser App können Sie das Baumdiagramm für den zweifachen Münzwurf näher erkunden.

Wir führen das Zufallsexperiment “Wurf einer fairen Münze” drei Mal aus (Abbildung 4.6). Dabei vereinbaren wir wieder, dass “Kopf” (K) als “Treffer” gilt und “Zahl” (Z) als “Niete”.

Abbildung 4.6: Wir werfen drei faire Münzen: Das dreifach wiederholte binäre Zufallexperiment

Beim Wurf von “fairen” Münzen gehen wir davon aus, dass Kenntnis des Ergebnis des 1. Wurfes unsere Einschätzung des Ergebnis des 2. Wurfes nicht verändert etc. Anders gesagt: Wir gehen von (stochastischer) Unabhängigkeit aus.

Für z.B. das Ereignis $A = {Z Z Z}$ gilt: $P r (A) = 1 / 2 \cdot 1 / 2 \cdot 1 / 2 = (1 / 2)^{3}$ . Da jeder Endknoten (jedes Blatt) gleichwahrscheinlich ist, ist die Wahrscheinlichkeit jedes Endknotens gleich.

Allgemeiner gilt: Für ein Zufallsexperiment, das aus $k$ Wiederholungen besteht und in jeder Wiederholung die Wahrscheinlichkeit $P r (X) = p$ ist, so ist die Wahrscheinlichkeit für einen Endkonten $P r (X^{k}) = p^{k}$ .

Tabelle 4.7: Ausgewählte Wahrscheinlichkeiten von Ereignissen im dreifachen Münzwurf

Ereignis	Pr
0K	1/2 * 1/2 * 1/2 = 1/8
1K	1/8 + 1/8 + 1/8 = 3/8
2K	3 * 1/8 = 3/8
3K	1/2 * 1/2 * 1/2 = 1/8

Da die Endknoten disjunkte Elementarereignisse sind, kann man ihre Wahrscheinlichkeit addieren, um zu anderen (zusammengesetzten) Ereignissen zu kommen, vgl. Tabelle 4.7.

Abbildung 4.2 versinnbildlicht nicht nur die Bedingtheit zweier Ereignisse, sondern auch die (Un-)Abhängigkeit zweier Ereignisse, $A$ und $B$ . In diesem Fall ist die Wahrscheinlichkeit von $A$ gleich $B$ : $P r (A) = P r (B) = .5$ . Man sieht, dass die Wahrscheinlichkeit von $A$ bzw. von $B$ jeweils die Hälfte der Fläche (der Gesamtfläche, d.h von $P r (Ω) = 1$ ) ausmacht. Die Schnittmenge der Fläche von $A$ und $B$ entspricht einem Viertel der Fläche: $P r (A B) = P r (A) \cdot P r (B) = 50 % \cdot 50 % = 25 % .$ In diesem Fall sind $A$ und $B$ unabhängig. Abbildung 4.2 zeigt weiterhin, dass gilt: $P r (A \cap B) = P (A) \cdot P (B) = P (B) \cdot P (A)$ . Man beachte, dass diese Formel nur bei Unabhängigkeit (von A und B) gilt.

4.6.2 Gemeinsame Wahrscheinlichkeit allgemeiner Ereignisse

Ein Baumdiagramm bietet sich zur Visualisierung allgemeiner abhängiger Ereignisse an, s. Abbildung 4.7.

Beispiel 4.16 In einer Urne befinden sich fünf Kugeln, von denen vier rot sind und eine blau ist.

Hier ist unsere Urne:

$R, R, R, R, B$

Wie groß ist die Wahrscheinlichkeit, dass bei zwei Ziehungen ohne Zurücklegen (ZOZ) zwei rote Kugeln gezogen werden (Bourier, 2011), S. 47. Ereignis A: “Kugel im 1. Zug hat die Farbe Rot”. Ereignis B: “Kugel im 2. Zug hat die Farbe Rot”.

Und jetzt ziehen wir. Hier ist das Baumdiagramm, s. Abbildung 4.7.

Abbildung 4.7: Baumdiagramm für ein zweistufiges Zufallsereignis, wobei der 2. Zug (Stufe) abhängig ist vom 1. Zug.

Wie man in Abbildung 4.7 nachrechnen kann gilt also: $P r (A \cap B) = P (A) \cdot P (B | A) = 4 / 5 \cdot 3 / 4 = 12 / 20 = 3 / 5 ◻$

Definition 4.6 (Gemeinsame Wahrscheinlichkeit) Die Wahrscheinlichkeit, dass zwei abhängige Ereignisse $A$ und $B$ gemeinsam eintreten, ist gleich dem Produkt der Wahrscheinlichkeit von $A$ und der bedingten Wahrscheinlichkeit von $B$ gegeben $A$ , s. Theorem 4.10. $◻$

Theorem 4.10 (Gemeinsame Wahrscheinlichkeit) $P r (A \cap B) = P r (A) \cdot P r (B | A) ◻$

Beispiel 4.17 (Kalt und Regen) Von McElreath (2020) stammt diese Verdeutlichung der gemeinsamen Wahrscheinlichkeit. Was ist die Wahrscheinlichkeit für das gemeinsame Auftreten von kalt ❄ und Regen ⛈️? Die Wahrscheinlichkeit für kalt und Regen ist die Wahrscheinlichkeit von Regen ⛈, wenn’s kalt ❄ ist mal die Wahrscheinlichkeit von Kälte ❄.

Ebenfalls gilt: Die Wahrscheinlichkeit für kalt und Regen ist die Wahrscheinlichkeit von Kälte ❄, wenn’s regnet ⛈️ mal die Wahrscheinlichkeit von Regen ⛈️.

Das Gesagte als Emoji-Gleichung ist in Gleichung 4.1 dargestellt.

$\begin{matrix} (4.1) & P r (❄ ️ und ⛈ ️) = P (⛈ ️ | ❄ ️) \cdot P (❄ ️) = P (❄ ️ | ⛈ ️) \cdot P (⛈ ️) \end{matrix}$

Man kann die “Gleichung drehen”¹¹, s. Gleichung 4.2.

$\begin{matrix} (4.2) & P r (❄ ️ und ⛈ ️) = P (⛈ ️ und ❄ ️) \end{matrix}$ $◻$

Beispiel 4.18 (Bertie Botts Bohnen jeder Geschmacksrichtung)

Sei bloß vorsichtig mit denen. Wenn sie sagen jede Geschmacksrichtung, dann meinen sie es auch - Du kriegst zwar alle gewöhnlichen wie Schokolade und Pfefferminz und Erdbeere, aber auch Spinat und Leber und Kutteln. George meint, er habe mal eine mit Popelgeschmack gehabt.“

— Ron Weasley zu Harry Potter¹²

In einem Beutel liegen $n = 20$ Bertie Botts Bohnen jeder Geschmacksrichtung. Uns wurde verraten, dass fast alle gut schmecken, also z.B. nach Schokolade, Pfefferminz oder Marmelade. Leider gibt es aber auch $x = 2$ furchtbar scheußliche Bohnen (Ohrenschmalz-Geschmacksrichtung oder Schlimmeres). Sie haben sich nun bereit erklärt, $k = 2$ Bohnen zu ziehen. Und zu essen, und zwar direkt und sofort! Also, jetzt heißt es tapfer sein. Ziehen und runter damit!

Wie groß ist die Wahrscheinlichkeit, genau eine scheußliche Bohne zu erwischen?

Es gibt 2 Pfade für 1 Treffer bei 2 Wiederholungen (Züge aus dem Beutel), s. Abbildung 4.8: Man kann im ersten Zug eine scheußliche Bohne erwischen, aber nicht im zweiten Zug. Oder man man im zweiten Zug Pech haben (aber nicht im ersten). Die Summe der Wahrscheinlichkeiten beider Pfade ist die Wahrscheinlichkeit für genau eine scheußliche Bohne, das sind 19%.

Abbildung 4.8: Baumdiagramm für ein ein zweistufiges Zufallsereignis: Bertie Botts Bohnen.

Code

Pfad1 <- 2/20 * 18/19  # scheußliche Bohne im 1. Zug
Pfad2 <- 18/20 * 2/19  # scheußliche Bohne im 2. Zug


Gesamt_Pr <- Pfad1 + Pfad2 
Gesamt_Pr
## [1] 0.19

Nutzen Sie diese App, um das auszuprobieren. Sie müssen in der App noch die Zahl der Bohnen ( $n$ ) und die Zahl der scheußlichen Bohnen ( $x$ ) einstellen. $◻$

4.6.3 Kettenregel

Definition 4.7 (Kettenregel) Allgemein gesagt, spricht man von der Kettenregel der Wahrscheinlichkeitsrechnung, wenn man die gemeinsame Wahrscheinlichkeit auf die bedingte zurückführt, s. Theorem 4.11. $◻$

Theorem 4.11 (Kettenregel) $P r (A \cap B) = P (A) \cdot P (B | A) = P (B) \cdot P (A | B) ◻$

In Worten: Die Wahrscheinlichkeit von $A$ gegeben $B$ ist gleich der Wahrscheinlichkeit von $A$ mal der Wahrscheinlichkeit von $B$ gegeben $A$ .

Übungsaufgabe 4.4 (Baumdiagramm sucht Problem) Überlegen Sie sich eine Problemstellung (Aufgabenstellung), die mit dieser Baumdiagramm-App gelöst werden kann. $◻$

Übungsaufgabe 4.5 (Peer Instruction: Dreifacher Münzwurf) Fünf Studierende unterhalten sich, wie man einen dreifachen Münzwurf verstehen kann mit dem Ergebnis von drei Treffern. Welcher Studierende liegt falsch? Gehen Sie von einer faire Münze aus und Unabhängigkeit der Würfe.

Wirft man die Münze drei Mal, so gibt es 6 Ergebnisse, die alle gleich wahrscheinlich sind. Aber nur ein Ergebnis ist gesucht, nämlich 3 von 3 Treffern. Also ist die Wahrscheinlichkeit 1/6, ca. 17%.
Man kann einfach einen Computer fragen, z.B. R mit dbinom(x = 3, size = 3, prob = 1/2), da kommt ungefähr 12% raus.
Wirft man die Münze drei Mal, so gibt es 8 Ergebnisse, die alle gleich wahrscheinlich sind. Aber nur ein Ergebnis ist gesucht, nämlich 3 von 3 Treffern. Also ist die Wahrscheinlichkeit 1/8, ca. 12,5%.
Wer rechnen kann, ist klar im Vorteil ${(\frac{1}{2})}^{3} = (\frac{1}{2^{3}}) = (\frac{1}{8})$
Holt mich hier raus! $◻$

4.7 Totale Wahrscheinlichkeit

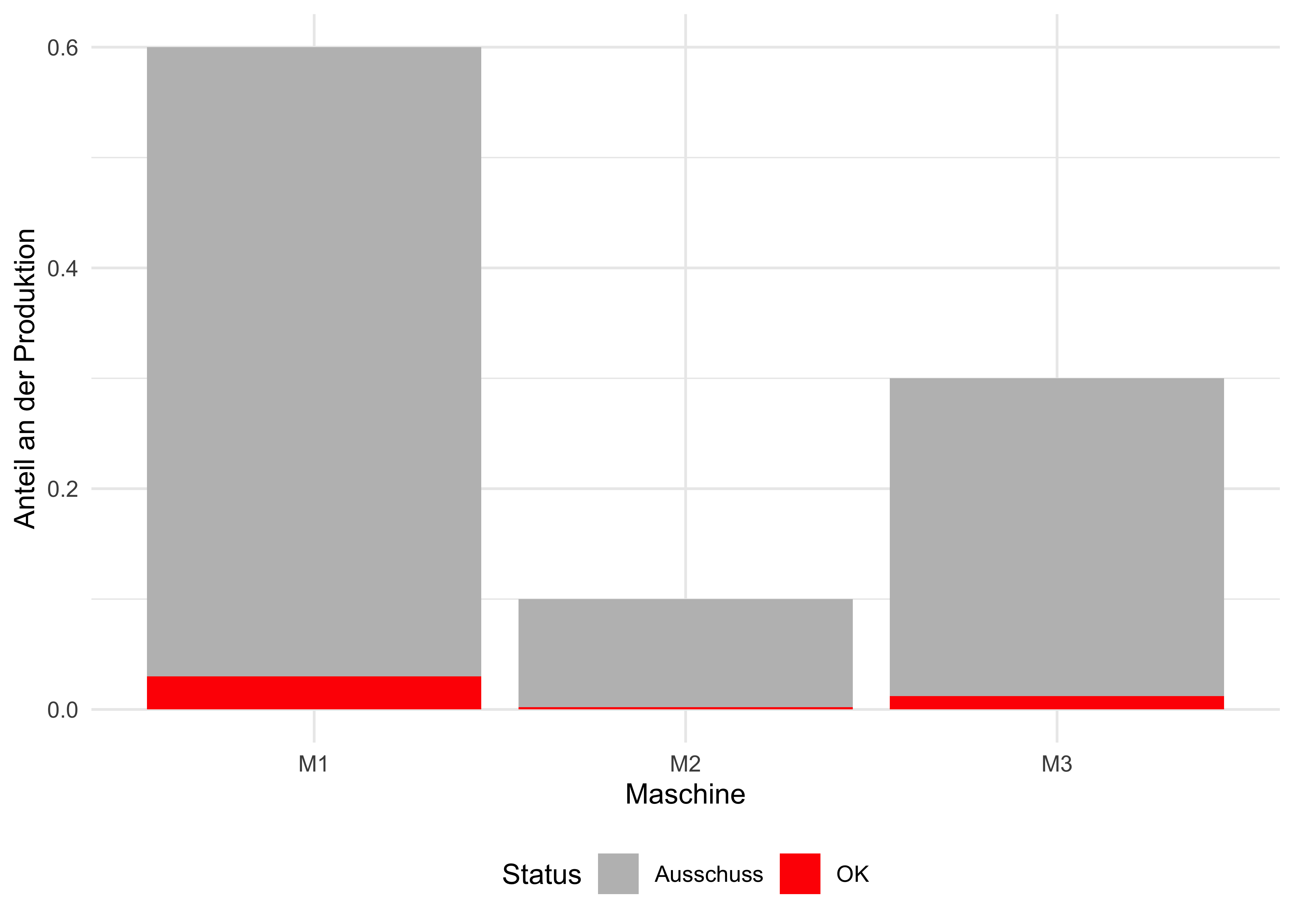
Beispiel 4.19 (Gesamter Ausschussanteil) Die folgende Aufgabe bezieht sich auf Bourier (2011), S. 56. Drei Maschinen ( $M_{1}, M_{2}, M_{3}$ ) produzieren einen Artikel. Die Maschinen haben einen Anteil an der Produktion von 60, 10 bzw. 30% und eine Ausschussquote von 5,2 bzw. 4%. Sei $M$ das Ereignis, dass ein Artikel von Maschine $M$ stammt, und $S$ (Schrott) das Ereignis, dass ein Artikel Ausschuss (Schrott) ist. Gesucht ist ist der Ausschussanteil insgesamt (über alle drei Maschinen). Anders gesagt: Wie hoch ist die Wahrscheinlichkeit $P r (S^{'})$ , dass ein zufällig gezogener Artikel Ausschuss ist? Abbildung 4.9 zeigt das Baumdiagramm für die Aufgabe. $◻$

Abbildung 4.9: Totale Wahrscheinlichkeit

Die Anteile an der Produktion und vom Ausschluss sind in Abbildung 4.10 verdeutlicht.

Code

source("R-code/plot_maschine_schrott.R")
plot_maschine_schrott

Abbildung 4.10: Anteile von Produktion und Ausschuss

Dazu addieren wir die Wahrscheinlichkeiten der relevanten Äste. Jeder Ast stellt wiederum das gemeinsame Auftreten der Ereignisse $M_{i}$ und $S$ dar.

Code

W_Ast1 <- 0.6 * 0.05  # Wahrscheinlichkeit für Ast 1
W_Ast2 <- 0.1 * 0.02  # ... Ast 2
W_Ast3 <- 0.3 * 0.04  # ... Ast 3
W_total <- W_Ast1 + W_Ast2 + W_Ast3  # totale W.
W_total
## [1] 0.044

Die totale Wahrscheinlichkeit (für Ausschuss) beträgt in diesem Beispiel also $P r (B^{'}) = 0.044 = 4.4 %$ .¹³

Definition 4.8 (Totale Wahrscheinlichkeit) Bilden die Ereignisse $M_{1}, M_{2}, . . ., M_{n}$ ein vollständiges Ereignissystem und ist $S$ ein beliebiges Ereignis dann gilt Theorem 4.12. $◻$

Theorem 4.12 (Totale Wahrscheinlichkeit) $P r (S^{'}) = \sum_{i = 1}^{n} P r (M_{i}) \cdot P r (S | M_{i}) . ◻$

In Worten: Die totale Wahrscheinlichkeit ist die Summe der gewichteten Teil-Wahrscheinlichkeiten.

In Abbildung 4.9 (Beispiel 4.19) gilt $P r (S^{'}) = 0.6 \cdot 0.05 + 0.1 \cdot 0.02 + 0.3 \cdot 0.04 = 0.03 + 0.002 + 0.012 = 0.04 . ◻$

Übungsaufgabe 4.6 (Bertie Botts Bohnen jeder Geschmacksrichtung, Teil 2) Es ist die gleich Aufgabe wie Beispiel 4.18, aber jetzt lautet die Frage: Wie groß ist die Wahrscheinlichkeit, mindestens eine scheußliche Bohne bei 3 Zügen zu erwischen?¹⁴ $◻$

4.7.1 Baumsammlung

Baumdiagramme sind ein hilfreiches Werkzeug für wiederholte Zufallsexperimente. Daher ist hier eine “Baumsammlung”¹⁵ zusammengestellt.

Sie werfen 1 Münze, Abbildung 3.2.
Sie werfen 2 Münzen, Abbildung 4.5.
Sie werfen 3 Münzen, Abbildung 4.6.
Sie werfen 4 Münzen, Abbildung 3.20.
Sie werfen 9 Münzen, 🤯 Abbildung 6.7.

4.8 Vertiefung

Bei Henze (2019) findet sich eine anspruchsvollere Einführung in das Rechnen mit Wahrscheinlichkeit; dieses Kapitel behandelt ein Teil des Stoffes der Kapitel 2 und 3 von Henze (2019).

Mit dieser App, die ein zweistufiges Baumdiagramm zeigt, können Sie das Verhalten von verschiedenen Arten von Wahrscheinlichkeiten weiter untersuchen.

Diese App lässt dich herausfinden, ob man wirklich krank ist, wenn der Arzt es bheauptet.

Das Video zu Bayes von 3b1b verdeutlicht das Vorgehen der Bayes-Methode auf einfache und anschauliche Weise.

Mittag & Schüller (2020) stellen in Kap. 11 die Grundlagen der Wahrscheinlichkeitstheorie vor. Ähnliche Darstellungen finden sich in einer großen Zahl an Lehrbüchern.

4.9 Aufgaben

Bearbeiten Sie die Aufgabe in der angegeben Literatur.

Die Webseite datenwerk.netlify.app stellt eine Reihe von einschlägigen Übungsaufgaben bereit. Sie können die Suchfunktion der Webseite nutzen, um die Aufgaben mit den folgenden Namen zu suchen:

4.9.1 Paper-Pencil-Aufgaben

4.9.2 Aufgaben, für die man einen Computer braucht

4.10 —

Die Wahrscheinlichkeit, keine 6 zu würfeln, liegt bei $2 / 3$ .↩︎
vermutlich gibt es noch mehr Annahmen, die wir uns explizit machen sollten.↩︎
genauer besehen sieht sie eher aus wie eine Grütze oder ein Brei↩︎
Sie schmeckt scheußlich.↩︎
$P r (L) .85; P r (\neg L) = .15; P r (B) = .81; P r (\neg B) = .19$ ↩︎
Exakte Gleichheit ist in dieser Welt empirisch schwer zu finden. Daher kann man vereinbaren, dass Unabhängigkeit erfüllt ist, wenn die Gleichheit “einigermaßen” oder “ziemlich” gilt, die Gleichheit gewissermaßen “praktisch bedeutsam” ist.↩︎
Vgl. Theorem 4.9 ↩︎
Wer Daten dazu hat oder eine Theorie, der melde sich bitte bei mir.↩︎
hier mit den zwei Ausprägungen DEU und USA↩︎
Daten von Our World in Data, https://ourworldindata.org/covid-deaths.↩︎
Der Multiplikationssatz ist symmetrisch↩︎
Quelle: https://harrypotter.fandom.com/de/wiki/Bertie_Botts_Bohnen_jeder_Geschmacksrichtung ↩︎
Einfacher als das Rechnen mit Wahrscheinlichkeiten ist es in solchen Fällen, wenn man anstelle von Wahrscheinlichkeiten absolute Häufigkeiten zum Rechnen verwendet.↩︎
Die Wahrscheinlichkeit keine scheußliche Bohne zu ziehen ist $17 / 20 \cdot 16 / 19 \cdot 15 / 18) \approx 0.6$ . Daher ist die gesuchte Wahrscheinlichkeit (mindestens eine scheußliche Bohne) das Komplement davon: $0.4$ .↩︎
Wald?↩︎