4 Verteilungen
4.1 Lernsteuerung
4.1.1 Position im Modulverlauf
Abbildung 1.1 gibt einen Überblick zum aktuellen Standort im Modulverlauf.
4.1.2 Lernziele
Nach Absolvieren des jeweiligen Kapitels sollen folgende Lernziele erreicht sein.
Sie können …
- den Begriff der Zufallsvariablen erläutern
- die Begriffe von Wahrscheinlichkeitsdichte und Verteilungsfunktion erläutern
- den Begriff einer Gleichverteilung erläutern
- den Begriff einer Binomialverteilung erläutern
- die Parameter einer Normalverteilung nennen und erläutern
- zentrale Konzepte in R umsetzen
4.1.3 Begleitliteratur
Der Stoff dieses Kapitels deckt sich (weitgehend) mit Bourier (2011), Kap. 6.1 und 6.3 sowie 7.1 und und 7.2.
4.1.4 Vorbereitung im Eigenstudium
Dieses Kapitel setzt einige Grundbegriffe voraus, wie im Buch Statistik1 vorgestellt, insbesondere im Kapitel “Rahmen”. Benötigt wird auch der Begriff der Normalverteilung sowie der Begriff der Quantile.
Lesen Sie selbständig, zusätzlich zum Stoff dieses Kapitels, noch in Bourier (2011) folgende Abschnitte:
- Kap. 6.1 (Zum Begriff Zufallsvariable)
- Kap. 6.3 (Stetige Zufallsvariablen)
- Kap. 7.1.1 (Binomialverteilung)
- Kap. 7.2.1 (Gleichverteilung)
- Kap. 7.2.3 (Normalverteilung)
Lösen Sie auch die Übungsaufgaben dazu.
Weitere Übungsaufgaben finden Sie im dazugehörigen Übungsbuch, Bourier (2022).
4.1.5 Prüfungsrelevanter Stoff
Beachten Sie, dass neben den Inhalten des Kapitels auch stets der vorzubereitende Stoff prüfungsrelevant ist.
4.1.6 Benötigte R-Pakete
4.1.7 Zentrale Begriffe
4.1.7.1 Eigenschaften von Zufallsvariablen
- Zufallsvariable (random variable)
- Diskret vs. stetig
- Wahrscheinlichkeitsdichte (Dichte, (probability) density, f)
- Wahrscheinlichkeitsfunktion (kumulierte Wahrscheinlichkeit, Wahrscheinlichkeitsmasse)
4.1.7.2 Verteilungen
- Gleichverteilung
- Normalverteilung
- Standardnormalverteilung
4.1.8 Begleitvideos
4.2 Zufallsvariable
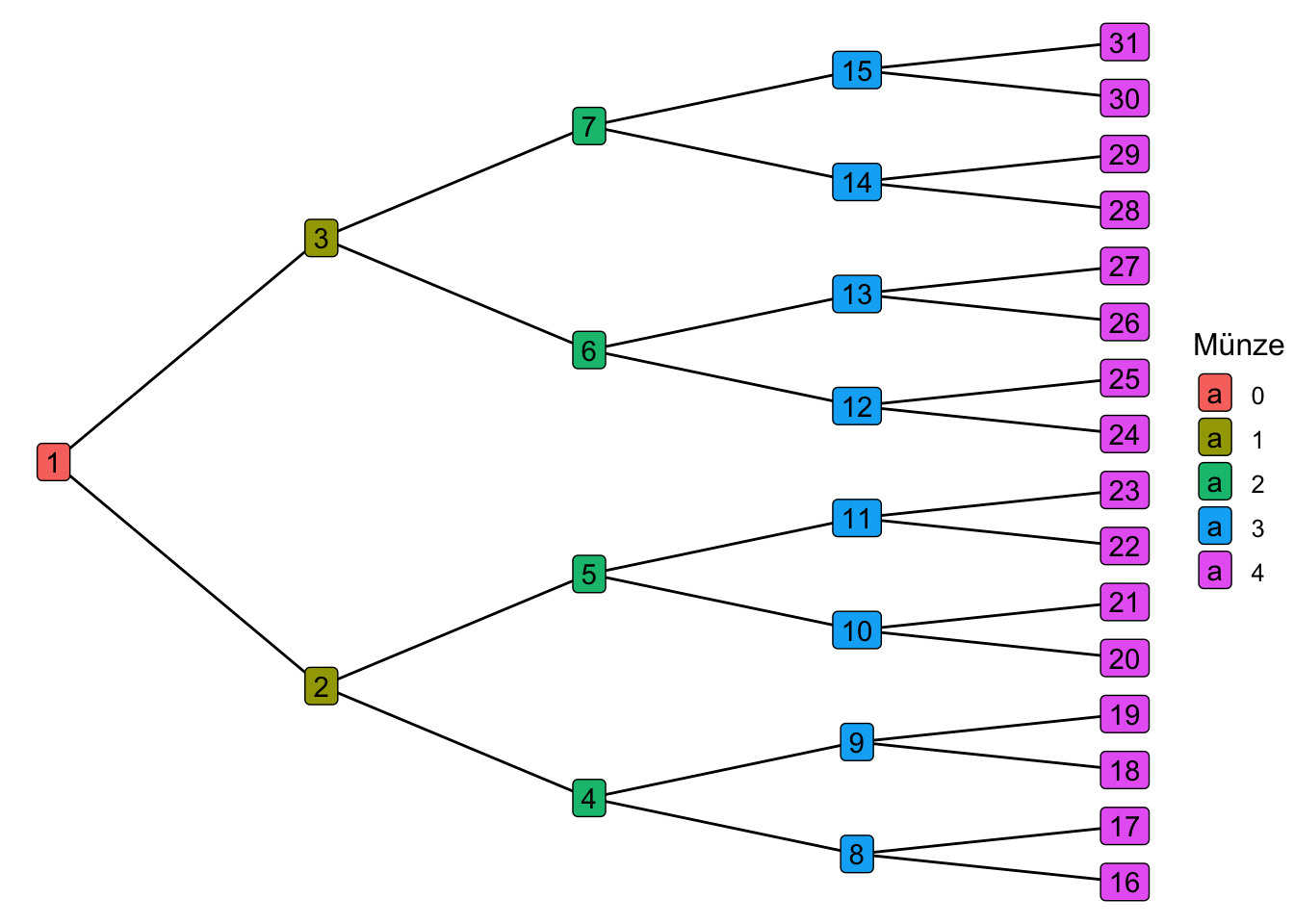
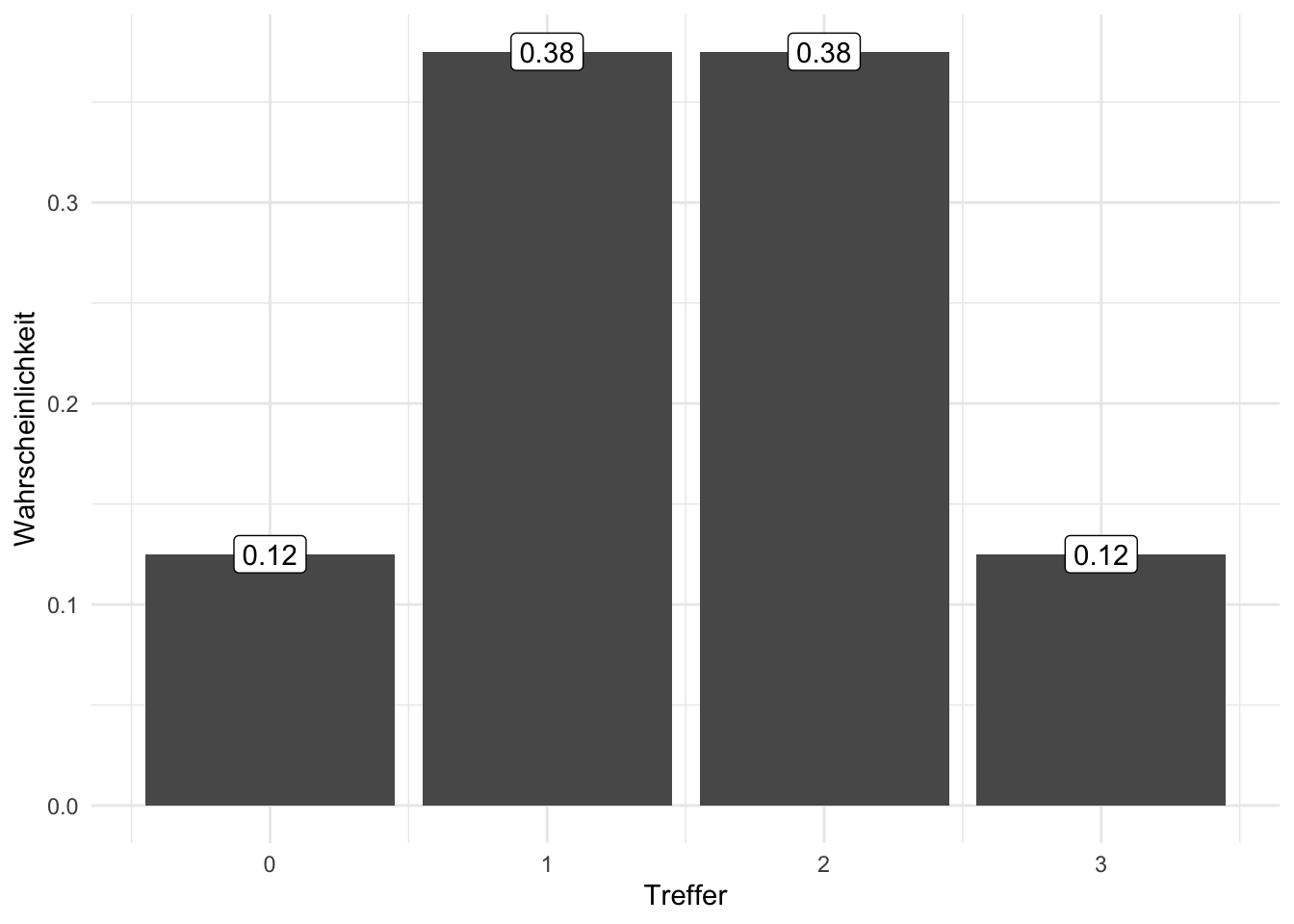
Beispiel 4.1 Schorsch sucht eine Betreuerin für seine Abschlussarbeit. An die ideale Betreuerin setzt er 4 Kriterien an: a) klare, schriftliche fixierte Rahmenbedingungen, b) viel Erfahrung, c) guten Ruf und d) interessante Forschungsinteressen. Je mehr dieser 4 Kriterien erfüllt sind, desto besser. Schorsch geht davon aus, dass die 4 Kriterien voneinander unabhängig sind (ob eines erfüllt ist oder nicht, ändert nichts an der Wahrscheinlichkeit eines anderen Kriteriums). Schorsch interessiert sich also für die Anzahl der erfüllten Kriterien, also eine Zahl von 0 bis 4. Er schätzt die Wahrscheinlichkeit für einen “Treffer” in jedem seiner 4 Kriterien auf 50%. Viel Glück, Schorsch! Sein Zufallsexperiment hat 16 Ausgänge (Knoten 16 bis 31), s. Abbildung 4.1 und Tabelle 4.1. Ganz schön komplex. Eigentlich würden ihm ja eine Darstellung mit 5 Ergebnissen, also der “Gutachter-Score” von 0 bis 4 ja reichen. Wie können wir es übersichtlicher für Schorsch?
Schorsch braucht also eine übersichtlichere Darstellung; die Zahl der Treffer und ihre Wahrscheinlichkeit würde ihm ganz reichen. In vielen Situationen ist man an der Anzahl der Treffer interessiert. Die Wahrscheinlichkeit für eine bestimmte Trefferanzahl bekommt man einfach durch Addieren der Wahrscheinlichkeiten der zugehörigen Elementarereignisse, s. Tabelle 4.1. Hier kommt die Zufallsvariable ins Spiel. Wir nutzen sie, um die Anzahl der Treffer in einem Zufallsexperiment zu zählen.
Definition 4.1 (Zufallsvariable) Die Zuordnung der Elementarereignisse eines Zufallsexperiments zu genau einer Zahl
Die den Elementarereignissen zugewiesenen Zahlen nennt man Realisationen oder Ausprägungen der Zufallsvariablen.
Beispiel 4.2 (Lotto) Ein Lottospiel hat ca. 14 Millionen Elementarereignisse. Die Zufallsvariable “Anzahl der Treffer” hat nur 7 Realisationen: 0,1,…,6.
Es hat sich eingebürgert, Zufallszahlen mit
Man schreibt für eine Zufallsvariable kurz:
Abbildung 4.2 stellt diese Abbildung dar.
Zufallsverteilungen kann im zwei Artein einteilen:
- diskrete Zufallsvariablen
- stetige Zufallsvariablen
4.2.1 Diskrete Zufallsvariable
4.2.1.1 Grundlagen
Eine diskrete Zufallsvariable ist dadurch gekennzeichnet, dass nur bestimmte Realisationen möglich sind, zumeist natürliche Zahlen, wie 0, 1, 2,…, . Abbildung 4.3 versinnbildlicht die Zufallsvariable des “Gutachter-Scores”, s. Beispiel 4.1.
Beispiel 4.3 (Diskrete Zufallsvariablen)
- Anzahl der Bewerbungen bis zum ersten Job-Interview
- Anzahl Anläufe bis zum Bestehen der Statistik-Klausur
- Anzahl der Absolventen an der HS Ansbach pro Jahr
- Anzahl Treffer beim Kauf von Losen
- Anzahl Betriebsunfälle
- Anzahl der Produkte in der Produktpalette
Beispiel 4.4 Der zweifache Würfelwurf ist ein typisches Lehrbuchbeispiel für eine diskrete Zufallsvariable. 1 Hier ist
.svg.png)
Wahrscheinlichkeitsverteilungen dienen dazu, den Realisationen einer Zufallsvariablen eine Wahrscheinlichkeit zuzuordnen.
Definition 4.2 (Diskrete Wahrscheinlichkeitsverteilung) Eine diskrete Wahrscheinlichkeitsverteilung der (diskreten) Zufallsvariablen
Beispiel 4.5 (Wahrscheinlichkeit des Geschlechts bei der Geburt) So hat die Variable Geschlecht eines Babies die beiden Ausprägungen Mädchen und Junge mit den Wahrscheinlichkeiten
Zwischen der deskriptiven Statistik und der Wahrscheinlichkeitstheorie bestehen enge Parallelen, Tabelle 4.2 stellt einige zentrale Konzepte gegenüber.
| Wahrscheinlichkeitstheorie | Desktiptive.Statistik |
|---|---|
| Zufallsvariable | Merkmal |
| Wahrscheinlichkeit | relative Häufigkeit, Anteil |
| Wahrscheinlichkeitsfunktion | einfache relative Häufigkeitsverteilung |
| Verteilungsfunktion | kumulierte relative Häufigkeitsverteilung |
| Erwartungswert | Mittelwert |
| Varianz | Varianz |
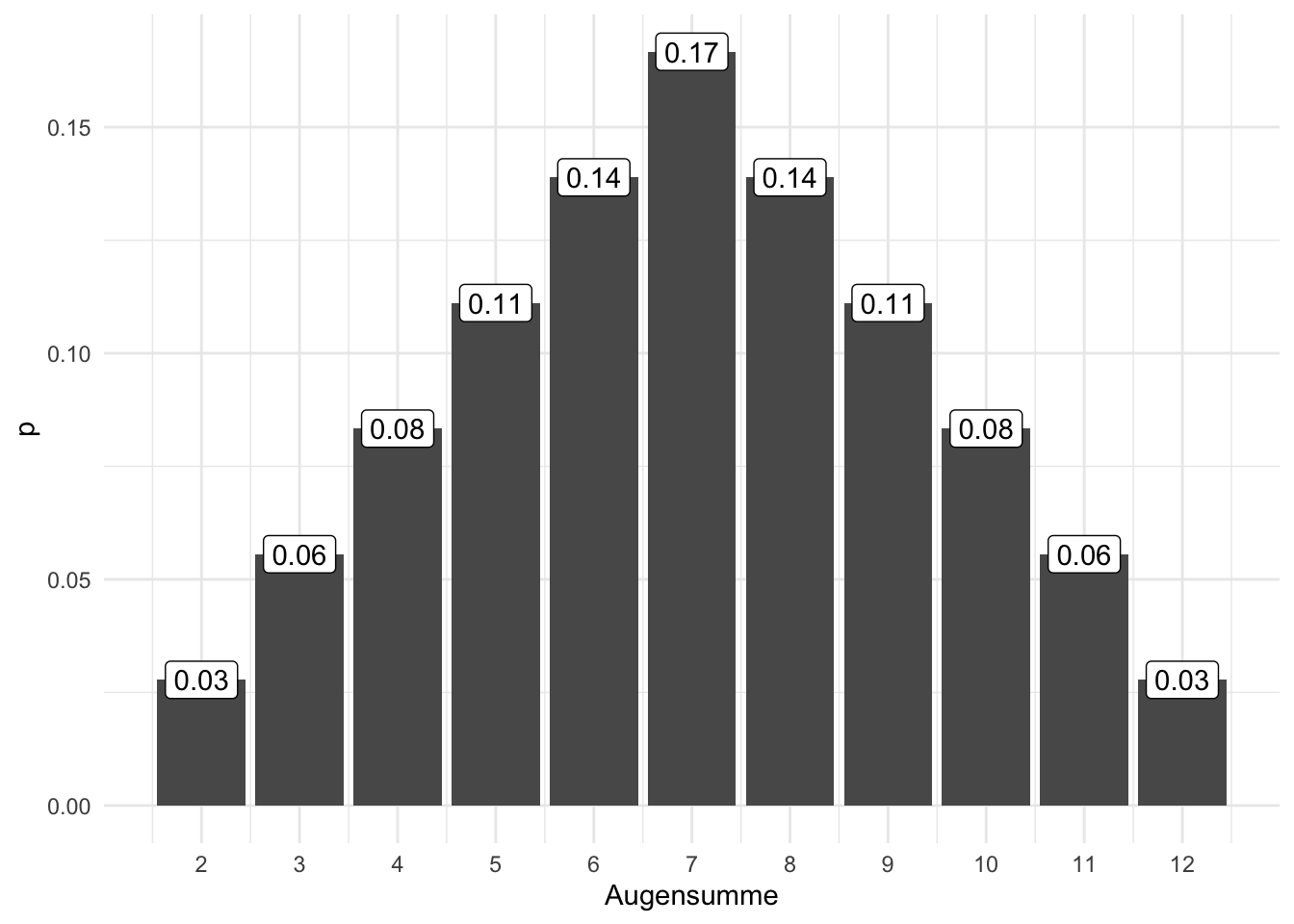
Eine Verteilung zeigt, welche Ausprägungen eine Variable aufweist und wie häufig bzw. wahrscheinlich diese sind. Einfach gesprochen veranschaulicht eine Balken- oder Histogramm eine Verteilung. Man unterscheidet Häufigkeitsverteilungen (s. Abb. Abbildung 4.6) von Wahrscheinlichkeitsverteilungen (Abb. Abbildung 4.5).
Beispiel 4.6 (Wahrscheinlichkeitsfunktion eines Würfels) Abbildung 4.7 zeigt die Wahrscheinlichkeitsfunktion eines einfachen Würfelwurfs.

Die Häufigkeitsverteilung eines diskreten Merkmals
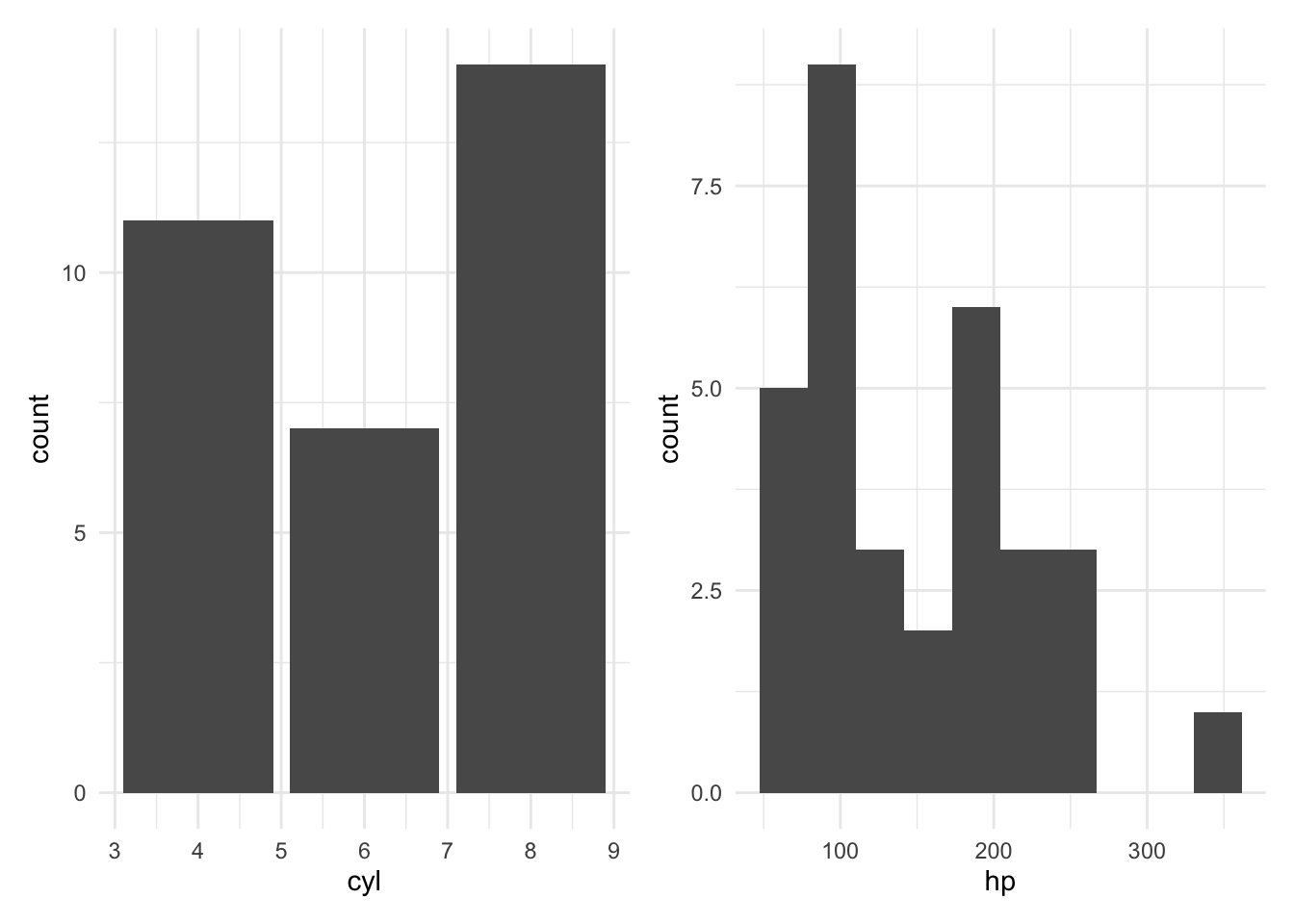
Abb. Abbildung 4.8, links, visualisiert die Häufigkeitsverteilung von cyl. Ein stetiges Merkmal, wie hp (PS-Zahl), lässt sich durch Klassenbildung in ein diskretes umwandeln (diskretisieren), s. Abb. Abbildung 4.8, rechts.
4.2.1.2 Wahrscheinlichkeitsfunktion
Definition 4.3 (Wahrscheinlichkeitsfunktion) Die Funktion
Beispiel 4.7 Die Wahrscheinlichkeitsfunktion für
Beispiel 4.8 Die Wahrscheinlichkeitsfunktion für
💡 Einfach gesprochen gibt die Wahrscheinlichkeitsfunktion die Wahrscheinlichkeit einer bestimmten Realisation einer Zufallsvariable an.
4.2.1.3 Verteilungsfunktion
Definition 4.4 (Verteilungsfunktion) Die Verteilungsfunktion
Die Berechnung von
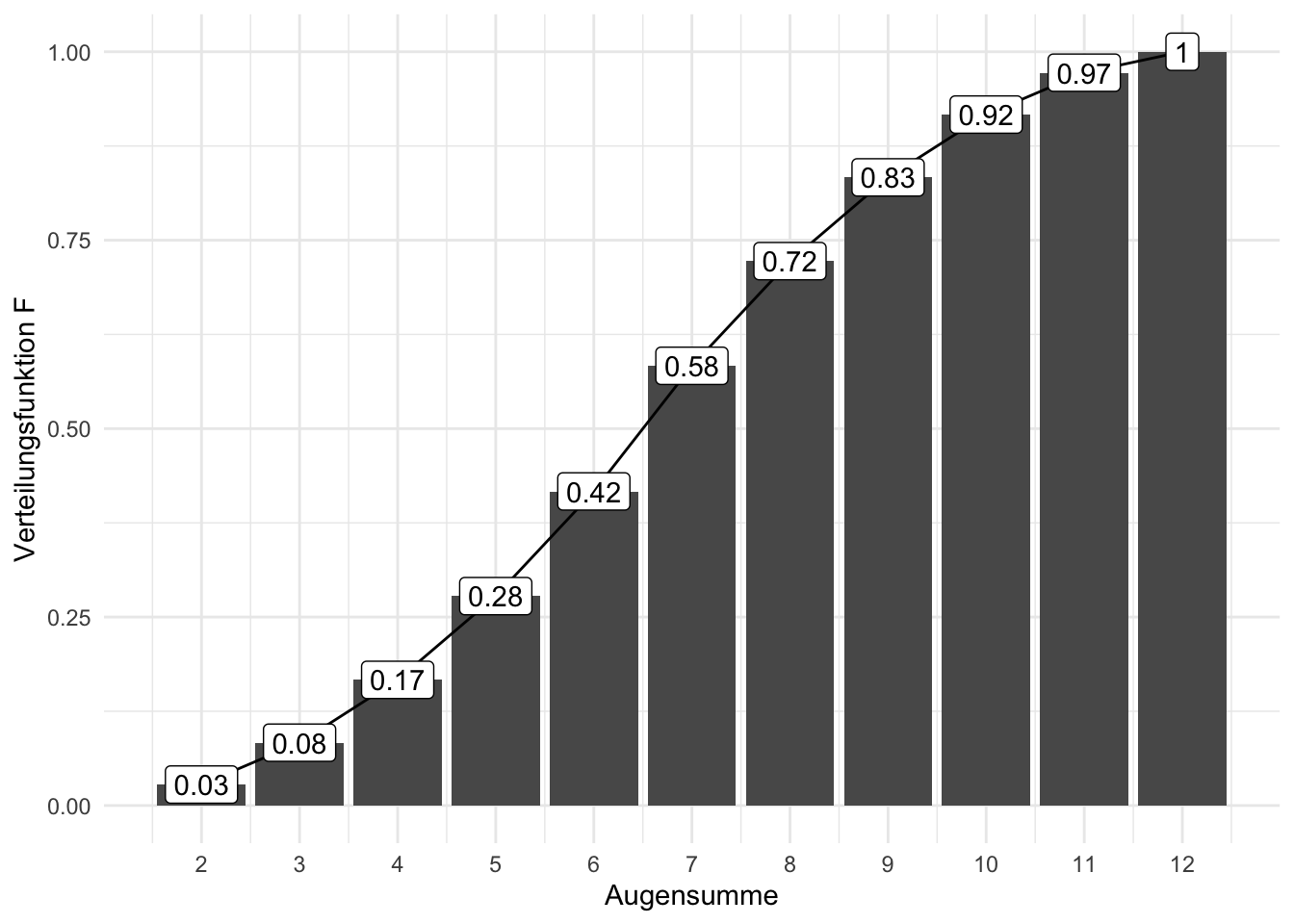
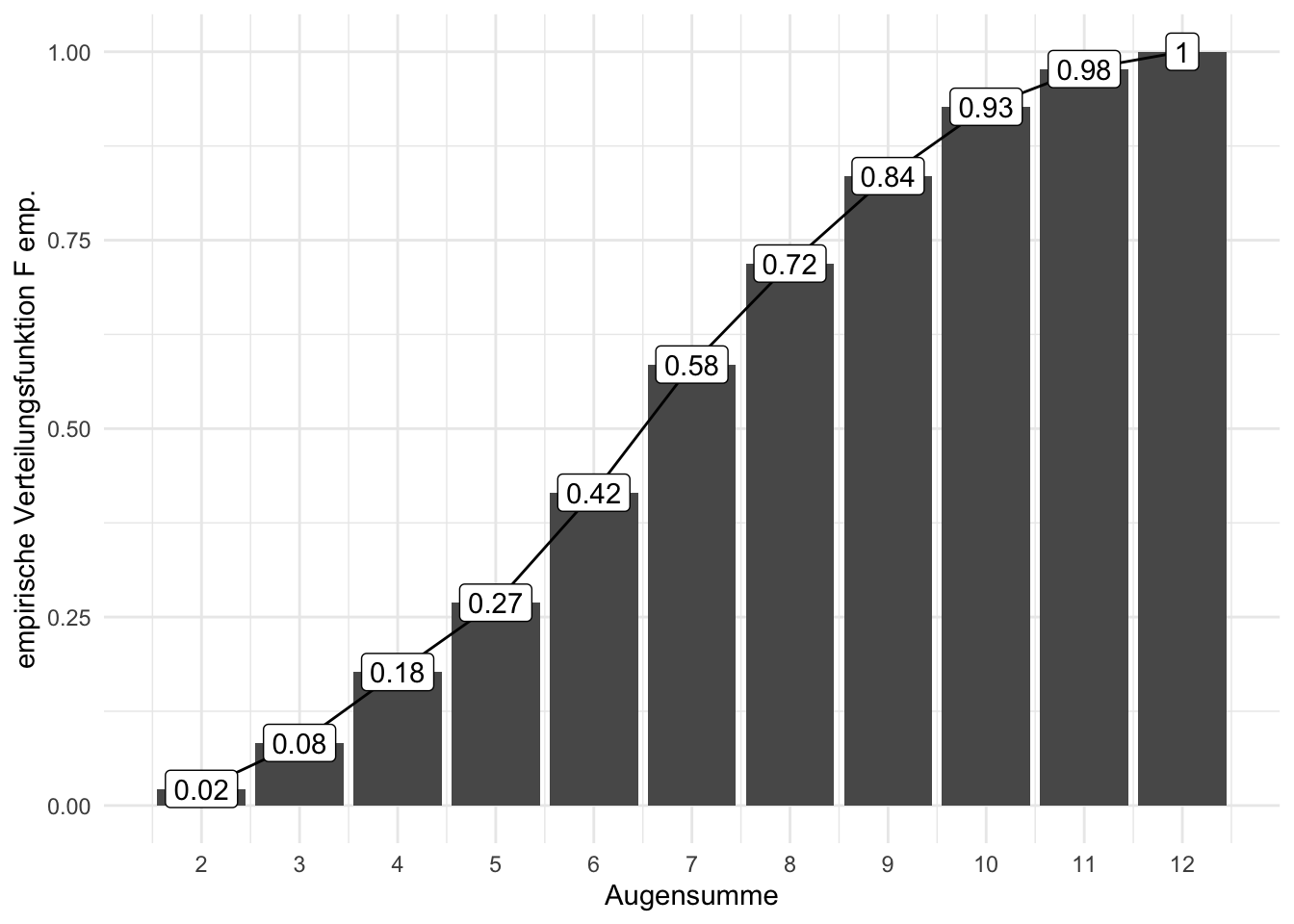
Die Verteilungsfunktion ist das Pendant zur kumulierten Häufigkeitsverteilung, vgl. Abbildung 4.9 und Abbildung 4.10: Was die kumulierte Häufigkeitsverteilung für Häufigkeiten ist, ist die Verteilungsfunktion für Wahrscheinlichkeiten.
4.2.2 Stetige Zufallsvariablen
📺 Verteilungen metrischer Zufallsvariablen
Abbildung 4.11 versinnbildlicht die stetige Zufallsvariable “Körpergröße”, die (theoretisch, in Annäherung) jeden beliebigen Wert zwischen 0 und (vielleicht) 2 Meter annehmen kann.
Definition 4.5 (Stetige Zufallsvariable) Eine stetige Zufallsvariable gleicht einer diskreten, nur dass alle Werte im Intervall erlaubt sind.
Beispiel 4.9
- Spritverbrauch
- Körpergewicht von Professoren
- Schnabellängen von Pinguinen
- Geschwindigkeit beim Geblitztwerden
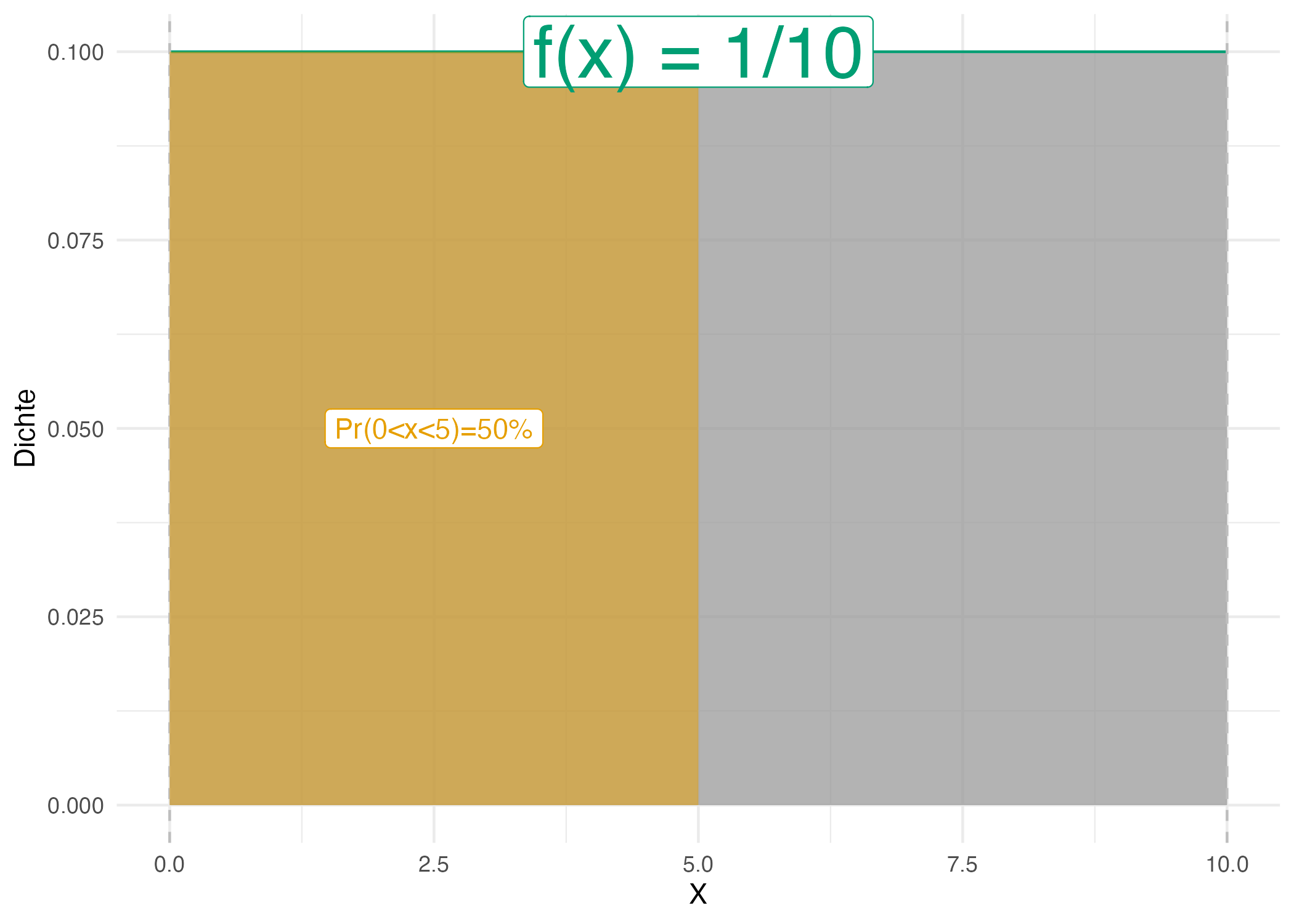
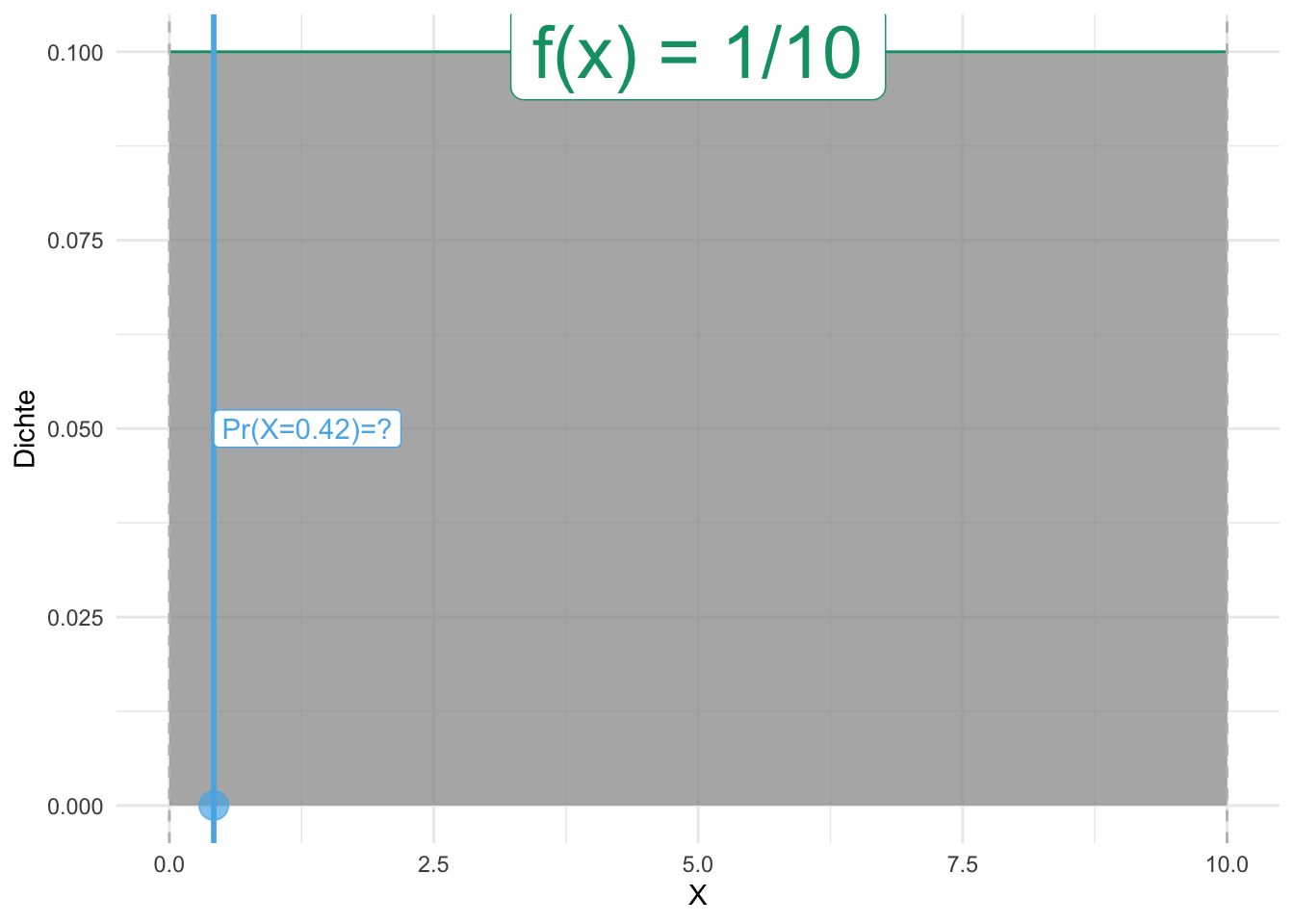
Übungsaufgabe 4.1 (Warten auf den Bus, 42 Sekunden) Sie stehen an der Bushaltestellen und warten auf den Bus. Langweilig. Da kommt Ihnen ein Gedanken in den Sinn: Wie hoch ist wohl die Wahrscheinlichkeit, dass Sie exakt 42 Sekunden auf den Bus warten müssen, s. Abbildung 4.13? Weiterhin überlegen Sie, dass davon auszugehen ist, dass jede Wartezeit zwischen 0 und 10 Minuten gleich wahrscheinlich ist. Spätestens nach 10 Minuten kommt der Bus, so ist die Taktung (extrem zuverlässig). Exakt heißt exakt, also nicht 42.1s, nicht 42.01s, nicht 42.001s, etc. bis zur x-ten Dezimale.
Nicht so einfach (?). Hingegen ist die Frage, wie hoch die Wahrscheinlichkeit ist, zwischen 0 und 5 Minuten auf den Bus zu warten (
Vergleicht man Abbildung 4.13 und Abbildung 4.12 kommt man (vielleicht) zu dem Schluss, dass die Wahrscheinlichkeit exakt 42s auf den Bus zu warten, praktisch Null ist. Der Grund ist, dass die Fläche des Intervalls gegen Null geht, wenn das Intervall immer schmäler wird. Aus diesem Grund kann man bei stetigen Zufallszahlen nicht von einer Wahrscheinlichkeit eines bestimmten Punktes
Was gleich ist in beiden Situationen (
Definition 4.6 (Wahrscheinlichkeitsdichte) Die Wahrscheinlichkeitsdichte
Die Wahrscheinlichkeitsdichte zeigt an, an welchen Stellen
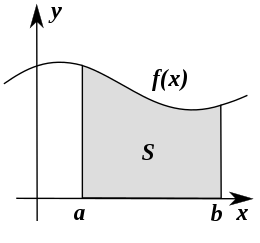
Definition 4.7 (Verteilungsfunktion) Die Verteilungsfunktion einer stetigen Zufallsvariablen gibt wie im diskreten Fall an, wie groß die Wahrscheinlichkeit für eine Realisation kleiner oder gleich einem vorgegebenen Realisationswert
Die Verteilungsfunktion
Definition 4.8 (Stetige Wahrscheinlichkeitsverteilung) Bei stetigen Zufallsvariablen
Beispiel 4.10 (Wahrscheinlichkeitsverteilung für die Körpergröße) So ist die Wahrscheinlichkeit, dass eine Person exakt 166,66666666… cm groß ist, (praktisch) Null. Man gibt stattdessen die Dichte der Wahrscheinlichkeit an: Das ist die Wahrscheinlichkeit(smasse) pro Einheit von
Für praktische Fragen berechnet man zumeist die Wahrscheinlichkeit von Intervallen, s. Abbildung 4.14.
4.3 Wichtige Verteilungen
Im Folgenden sind einige wichtige Verteilungen aufgeführt, die in diesem Skript (und in der Statistik und Wahrscheinlichkeitstheorie) eine zentrale Rolle spielen.
4.4 Gleichverteilung
4.4.1 Indifferenz als Grundlage
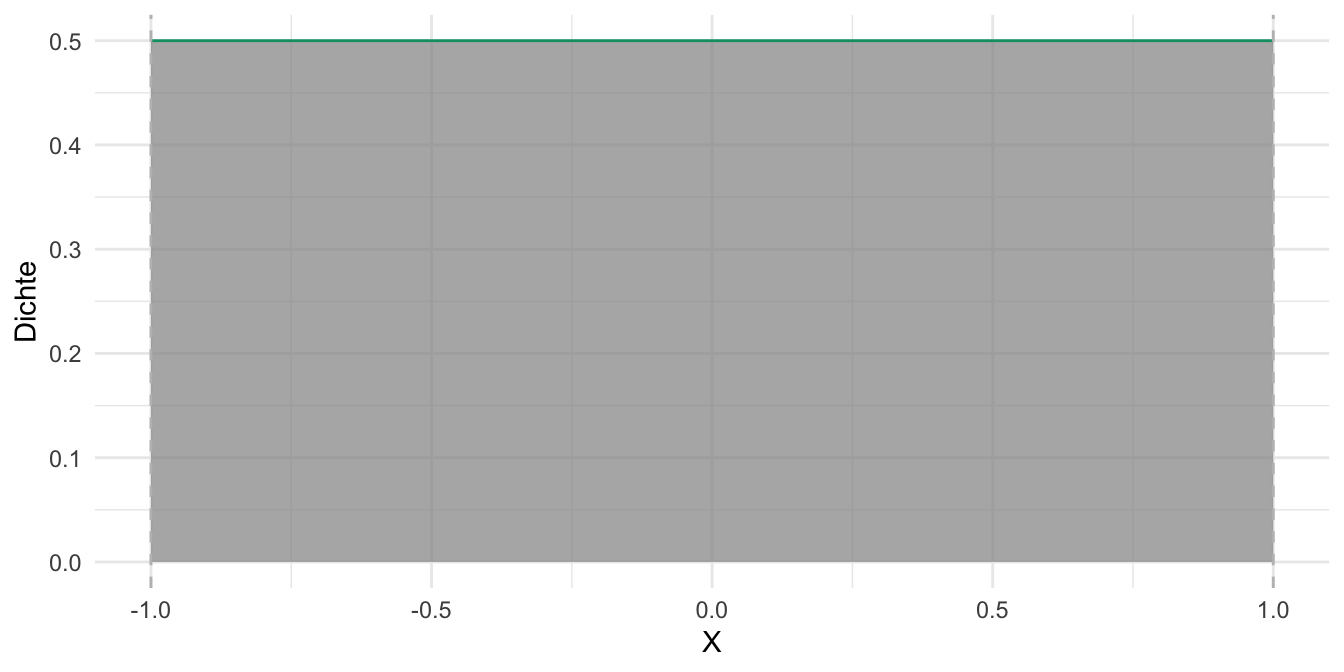
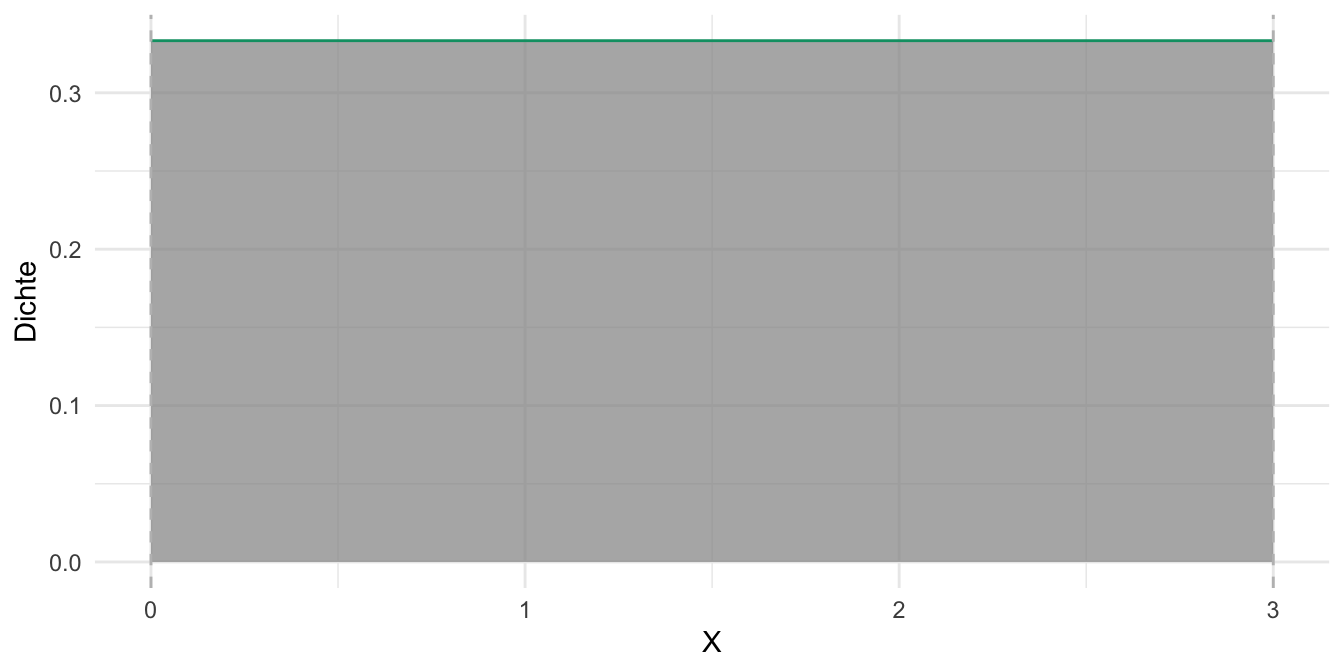
Eine Gleichverteilung nimmt an, dass jeder Wert im Ergebnisraum der zugehörigen Zufallsvariable gleichwahrscheinlich ist. Wenn man keinen hinreichenden Grund hat, eine Realisation einer Zufallsvariablen für plausibler als einen anderen zu halten, ist eine Gleichverteilung eine passende Verteilung. Gleichverteilungen gibt es im diskreten und im stetigen Fall.
Abb. Abbildung 4.16 zeigt ein Beispiel für eine (stetige) Gleichverteilung.
Abbildung 4.16, links: Bei
4.4.2 Simulation
Möchte man die Verteilungsfunktion einer stetigen Zufallsvariablen berechnen, kann die Mathe ganz schön kompliziert werden, schließlich muss man Integrale lösen. Aber es gibt einen Trick, wie man die Sache stark vereinfachen kann: man simuliert die Verteilung. Was bedeutet das?
Angenommen, die Wartezeit auf einen Bus ist gleichverteilt (engl. uniform distribution); der Bus kommt regelmäßig und pünktlich alle 10 Minuten. Die minimale Wartezeit beträgt also 0 Minuten und die maximale 10 Minuten. Nennen wir die zugehörige Zufallsvariable
Eine gleichverteilte Zufallsvariable
Ja, das sieht fancy aus, ist aber dafür schön kurz, aber wo ist der versprochene Trick zum Vereinfachen? Kommt gleich, Moment.
Eine Frage könnte nun lauten, wie groß ist die Wahrscheinlichkeit, dass man zwischen 3 und 5 Minuten auf den Bus warten muss? Achtung: Hier ist der Trick. Nämlich, dass wir Integralrechnung gegen stumpfes Zählen eintauschen.
Computer (und damit R) haben eingebaute Funktionen, die eine beliebige Zufallszahl ziehen können, zum Beispiel gleichverteilte. Auf Errisch heißt das Zauberwort runif(): Mit dieser Funktion kann man gleichverteilte Zufallszahlen ziehen. Einfach gesprochen: Der Computer greift in eine Säckchen mit Murmeln, die mit verschiedenen Zahlen beschriftet sind, wobei alle Zahlen gleich häufig sind, und greift eine heraus.
Auf Deutsch heißt das:
👨🏫 “Hey R, ich hätte gerne eine (daher
n = 1) Zufallszahl (r wie random), die gleichverteilt ist (uniform) mitmin = 0undmax = 10.
🤖 Jawohl, oh herrliches Leberwesen
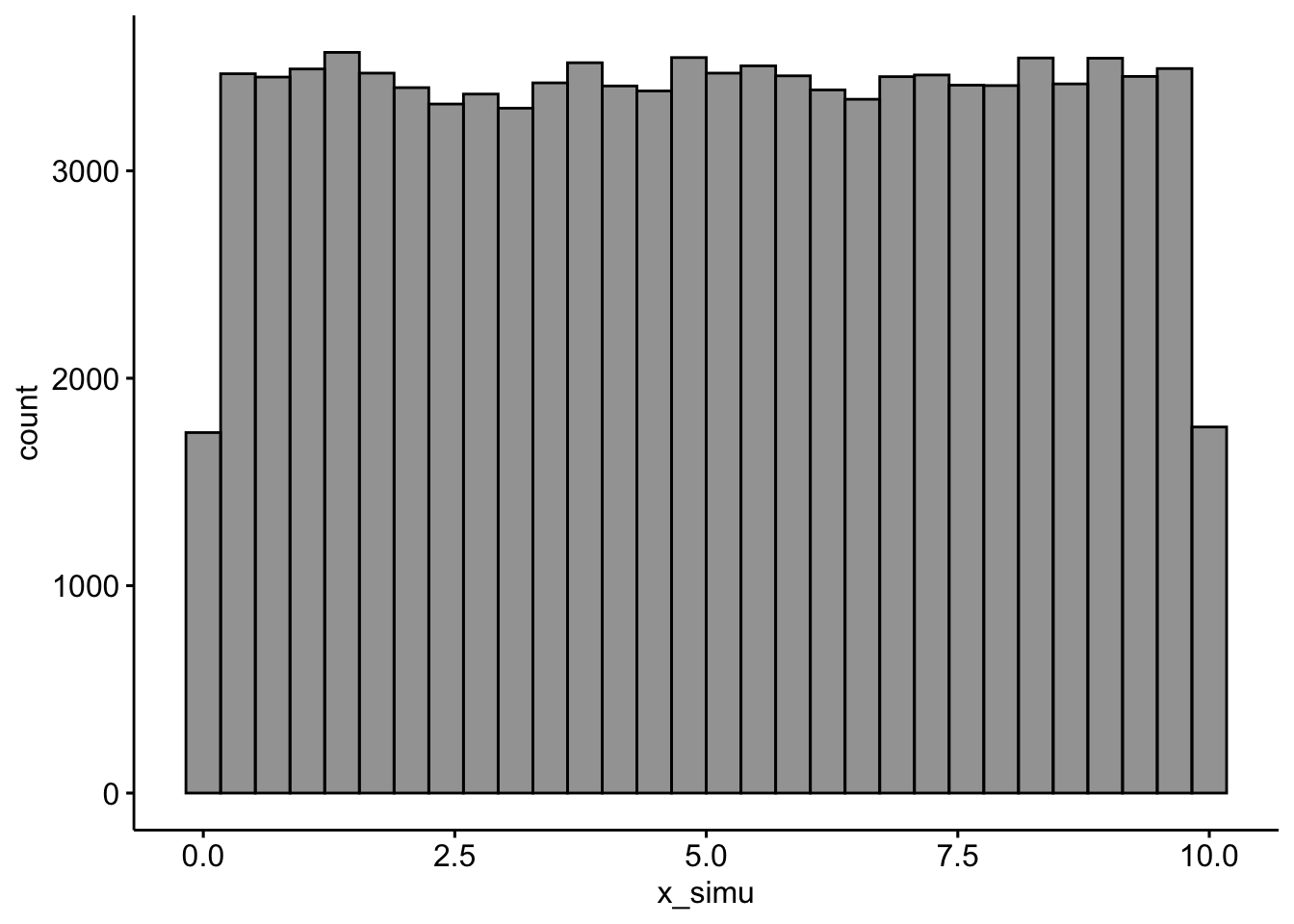
(Zu) anschaulich gesprochen: R hat den Bus kommen lassen und es hat gut 9.1 Minuten gedauert, bis er da war. Achtung, jetzt kommt’s: Jetzt lassen wir R mal 1e5 auf Computersprech) Busse vorfahren. R soll jedes Mal notieren, wie lange man auf den Bus warten musste.3
Code
x_simu <- runif(n = 1e5, min = 0, max = 10)Schauen wir uns die Verteilung an, s. Abbildung 4.17.4
Code
library(ggpubr)
gghistogram(x_simu_df, x = "x_simu", fill = "grey20")Okay, unsere Verteilung sieht nicht exakt gleichverteilt, aber einigermaßen. Gut genug für unsere Zwecke!
So, und jetzt kommt das Ernten. Wir können jetzt nämlich einfach zählen (count()), um die Antwort auf unsere Frage (der Wartezeit 3-5 Min.) zu erhalten, s. Tabelle 4.4.
Das Zeichen & ist das logische UND, also die Schnittmenge der zwei Mengen
Wie man sieht, fallen ca. 20% der Stichproben in den entsprechenden Bereich.
Da viele Probleme, wenn sie komplexer werden, kaum noch “analytisch” (d.h. wie Ausrechnen von Integralen) lösbar sind, greift man in der modernen (Analyse-)Welt oft lieber auf Simulationsverfahren zurück - Dank sei den schnellen Rechnern. Für uns Menschen ist damit die Aufgabe des Integrierens auf schnödes Zählen zurückgeführt.
4.5 Binomialverteilung
4.5.1 Grundlagen
Definition 4.9 (Binomialverteilung) Die Binomialverteilung dient zur Darstellung der Wahrscheinlichkeit der Ergebnisse eines
Für eine binomialverteilte Zufallsvariable
Theorem 4.1 (Notation für eine binomialverteilte Zufallsvariable)
Beispiel 4.11 Anwendungsbeispiele: Wie viele defekte Teile sind in einer Stichprobe von produzierten Schrauben zu erwarten? Wie wahrscheinlich ist es, dass das neue Blutdruck-Medikament einer bestimmten Anzahl von Menschen hilft? Wie viele Personen stimmen in einer Umfrage der Frage “Ich halte die öffentlich-rechtlichen Sender für wichtig.” zu?
Stellen wir uns eine Kistchen7 mit sehr vielen8 Losen vor, darunter 2/5 Treffer (Gewinn) und 3/5 Nieten, s. Abb. Abbildung 4.18. Der Versuch läuft so ab: Wir ziehen ein Los, schauen ob es ein Treffer ist oder nicht, legen es zurück und ziehen erneut.9 Jetzt ziehen wir z.B. drei Lose. Wie groß ist die Wahrscheinlichkeit, davon 2 Treffer zu erzielen (egal in welcher Reihenfolge)?
Praktischerweise ist die Binomialverteilung in R eingebaut,
hier ist Pseudocode für Ihre Anwendung, s. Listing 4.1.
4.5.2 Möglichkeiten zählen
Beispiel 4.12 (Drei Lose gekauft, davon zwei Treffer?) Wie groß ist die Wahrscheinlichkeit
Mit Blick auf Beispiel 4.12: Wir könnten jetzt ein Baumdiagramm zeichnen und pro Pfad die Wahrscheinlichkeit ausrechnen (Multiplikationssatz, Theorem 3.11), vgl. Abbildung 4.20. Die Summe der Wahrscheinlichkeiten der Pfade ist dann die gesuchte Wahrscheinlichkeit (Additionssatz, Theorem 3.3). Diagramme zeichnen ist einfach, dauert aber.
Beachtet man die verschiedenen Reihenfolgen nicht (in Abbildung 4.20), so zählt man 3 günstige Pfade (vgl. Abbildung 4.19):
- TTN
- TNT
- NTT.
Wir haben also die Möglichkeiten (2 Treffer und 1 Niete zu erhalten)
- ohne Beachtung der Reihenfolge und
- ohne Zurücklegen (der Möglichkeiten)
gezählt.
Schneller geht es, wenn man rechnet. Wir könnten auch R auffordern, die Anzahl der günstigen Pfade zu berechnen, s. Theorem 4.3:
Code
choose(3,2)
## [1] 34.5.3 Anzahl Pfade mal Pfad-Wahrscheinlichkeit
In diesem Fall ist die Wahrscheinlichkeit eines (günstigen) Pfades,
Code
p_a = (2/5)^2 * (3/5)^1
p_a
## [1] 0.096Damit ist die Wahrscheinlichkeit des gesuchten Ereignisses
Code
p_a_strich = 3 * p_a
p_a_strich
## [1] 0.288Die Wahrscheinlichkeit, bei 3 Zügen 2 Treffer zu erzielen, beträgt also ca. 29%, vgl. Gleichung 4.2.
Dabei steht
4.5.4 Rechnen mit der Binomialverteilung
Die Binomialverteilung ist in R eingebaut; man kann sich leicht entsprechende Wahrscheinlichkeiten ausrechnen lassen. Das ist komfortabler als selber rechnen.
Code
dbinom(x = 2, size = 3, prob = 2/5)
## [1] 0.288Die Wahrscheinlichkeit, 2 Treffer bei 3 Zügen zu erzielen mit
Dabei gehen wir davon aus, dass die Wahrscheinlichkeit eines Treffers stets
Beispiel 4.13 (Lotto) Wie viele Zahlenkombinationen gibt es im Lotto für 6 Richtige? Der Binomialkoeffizient verrät es uns:
Beispiel 4.14 Wie viele Möglichkeiten gibt es, 2 Treffer bei 4 Zügen zu erzielen?
- TTNN, 2. TNTN, 3. TNNT, 4. NTTN ,5. NTNT, 6. NNTT.
Es sind also 6 Möglichkeiten.
In R kann man sich die Fakultät mit dem Befehl factorial ausrechnen lassen. Der R-Befehl choose berechnet den Binomialkoeffizienten.10
Code
choose(4, 2)
## [1] 6Beispiel 4.15 Hier sind die 10 Kombinationen, um aus 5 Losen genau 2 Treffer und 3 Nieten zu ziehen:
TTNNN, TNTNN, TNNTN, TNNNT, NTTNN, NTNTN, NTNNT, NNTTN, NNTNT, NNNTT
Code
choose(5, 2)
## [1] 10Beispiel 4.16 (Beförderung) Aus einem Team mit 25 Personen sollen 11 Personen befördert werden. Wie viele mögliche Kombinationen (von beförderten Personen) können gebildet werden?
Code
choose(n = 25, k = 11)
## [1] 4457400Es gibt 4457400 Kombinationen von Teams; dabei ist die Reihenfolge der Ziehung nicht berücksichtigt.
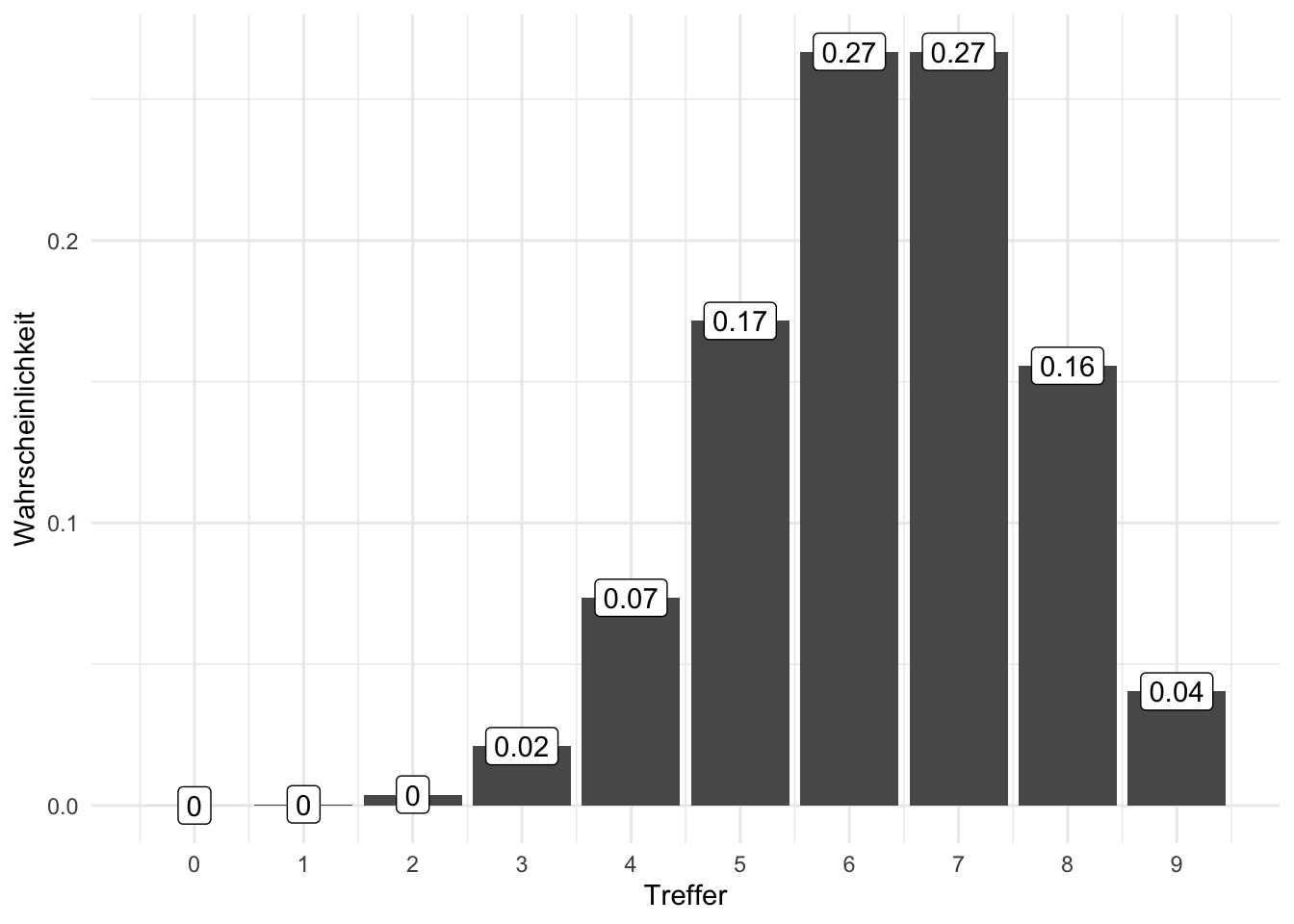
Beispiel 4.17 (Pumpstation-Beispiel zur Binomialverteilung) In einer Pumpstation arbeiten 7 Motoren, die wir als identisch annehmen. Mit einer Wahrscheinlichkeit von 5% fällt ein Motor aus und ist für den Rest des Tages nicht einsatzbereit. Der Betrieb kann aufrecht erhalten werden, solange mindestens 5 Motoren arbeiten. Wie groß ist die Wahrscheinlichkeit, dass die Pumpstation aus dem Betrieb fällt?
Lassen wir R mal
Code
dbinom(x = 5, size = 7, prob = .95)
## [1] 0.0406235Es gilt also
dbinom() steht für die Wahrscheinlichkeitsdichte (im diskreten Fall, wie hier, Wahrscheinlichkeitsfunktion genannt) und binom für die Binomialverteilung. x gibt die Anzahl der Treffer an (das gesuchte Ereignis, hier 5 Motoren arbeiten); size gibt die Stichprobengröße an (hier 7 Motoren).
Damit gilt:
Berechnen wir zunächst die Wahrscheinlichkeit, dass 5,6 oder 7 Motoren laufen mit Hilfe der Binomialverteilung.
Das sind 0.04, 0.26, 0.7.
Die gesuchte Wahrscheinlichkeit, p_mind_5, ist die Summe der drei Einzelwahrscheinlichkeiten.
Code
p_mind_5 <- p_5 + p_6 + p_7
p_mind_5
## [1] 0.996243Die Wahrscheinlichkeit, dass mind. 5 Motoren arbeiten beträgt also 0.9962.
Das komplementäre Ereignis zu diesem Ereignis ist, dass nicht mind. 5 Motoren arbeiten, also höchstens 4 und es daher zu einem Ausfall kommt. Es gilt also
Code
p_weniger_als_4 <- 1 - p_mind_5
p_weniger_als_4
## [1] 0.003757043Das sind also 0.0038 oder 0.0003, also 0.03% Wahrscheinlichkeit, dass die Pumpstation ausfällt.
Alternativ kann man mit der Verteilungsfunktion pbinom() rechnen, die
In R kann man die Funktion pbinom() nutzen (p für (kumulierte) Wahrscheinlichkeit), um die Verteilungsfunktion der Binomialverteilung zu berechnen:
Code
pbinom(q = 4, size = 7, prob = .95)
## [1] 0.003757043q = 4 steht für size = 7 meint die Stichprobengröße, hier 7 Motoren; prob gibt die Trefferwahrscheinlichkeit an.
Die Funktion, die die Wahrscheinlichkeit dafür angibt, dass die diskrete Zufallsvariable
4.5.4.1 Formel der Binomialverteilung
Theorem 4.2 zeigt die mathematische Definition der Binomialverteilung. Dabei liegt immer ein Zufallsversuch mit
Theorem 4.2 (Binomialverteilung)
Theorem 4.2 kann wie folgt auf Deutsch übersetzen:
Die Wahrscheinlichkeit für das Ereignis
gegeben und berechnet als Produkt von zwei Termen. Der erste Term ist der Quotient von der Fakultät von n im Zähler und im Nenner das Produkt von erstens der Fakultät von k mit zweitens der Fakultät von (n-k). Der zweite Term ist das Produkt von p hoch k mal der komplementären Wahrscheinlichkeit von p hoch (n-k).
Oder noch kürzer:
Die Wahrscheinlichkeit für das Ereignis “X” gegeben p und k berechnet als Produkt von zwei Termen. Erstens der Anzahl der günstigen Pfade, k und zweitens der Wahrscheinlichkeit für einen günstigen Pfad, P(A).
Die Anzahl der (günstigen) Pfade kann man mit dem Binomialkoeffizient ausrechnen, den man so darstellt, s. Theorem 4.3.12
Definition 4.10 (Binomialkoeffizient) Der Binomialkoeffizient gibt an, auf wie vielen verschiedenen Arten man aus einer Menge von
Theorem 4.3 (Binomialkoeffizient)
Lies: “Wähle aus
Puh, Formeln sind vielleicht doch ganz praktisch, wenn man sich diese lange Übersetzung der Formel in Prosa duchliest. Noch praktischer ist es aber, dass es Rechenmaschinen gibt, die die Formel kennen und für uns ausrechnen.
Beispiel 4.18 (Klausur mit 20-Richtig-Falsch-Fragen) Ei Professi stellt einen Klausur mit 20 Richtig-Falsch-Fragen. Wie groß ist die Wahrscheinlichkeit, durch bloßes Münze werfen genau 15 Fragen richtig zu raten?13
Code
# Wskt für genau 15 Treffer bei 20 Versuchen mit einer fairen Münze:
dbinom(x = 15, size = 20, prob = .5)
## [1] 0.01478577Um höchstens 15 Treffer zu erzielen, müssten wir die Wahrscheinlichkeiten von 0 bis 15 Treffern addieren.
Praktischerweise gibt es einen R-Befehl, der das für uns übernimmt: pbinom.
Code
pbinom(q = 15, size = 20, prob = .5)
## [1] 0.994091Die Wahrscheinlichkeit 0, 1, 2, … oder 15 Treffer zu erzielen, liegt laut Binomialverteilung mit pbinom bei gut 99%.
Beispiel 4.19 (3 Münzwürfe mit 3 Treffern) Was ist die Wahrscheinlichkeit bei 3 Münzwürfen (genau) 3 Treffer (Kopf) zu erzielen, s. Abbildung 4.22?
Das ist eine Frage an die Binomialverteilung; in R kann man das mit der Funktion dbinom beantworten.
Code
dbinom(x = 3, size = 3, prob = 1/2)
## [1] 0.125Die Lösung lautet also
Man kann sich auch vor Augen führen, dass es genau 1 günstigen Pfad gibt, nämlich TTT. Nach dem Multiplikationssatz gilt also:
Code
loesung <- (1/2)^3
loesung
## [1] 0.125Übungsaufgabe 4.2 🏋️️ Was fällt Ihnen bei der Binomialverteilung auf? Ist sie symmetrisch? Verändert sich die Wahrscheinlichkeit linear?
4.5.5 Vertiefung
4.5.5.1 Logarithmus
Ein Logarithmus ist die Umkehrung der Potenzierung.
Der Logarithmus beantwortet folgende Frage: Mit welchem Exponenten muss ich eine bestimmte Zahl (die Basis) potenzieren, um eine andere Zahl zu erhalten? Die Antwort auf diese Frage ist der Logarithmus.
Formal ausgedrückt:
Definition 4.11 (Logarithmus) Der Logarithmus von einer Zahl
Theorem 4.4 (Logarithmus)
Der Logarithmus zur Basis 214 gibt die “Verdopplungen” bzw. “Halbierungen” der Wahrscheinlichkeit an, wobei
Beispiel 4.20
Code
log(.5, base = 2)
## [1] -11/2 ist genau “minus 1 Verdopplung” von 1 entfernt, d.h. eine Halbierung.
Code
log(1/4, base = 2)
## [1] -21/4 ist genau “minus 2 Verdopplungen” von 1 entfernt, d.h. zwei Halbierungen.
Code
log(1/8, base = 2)
## [1] -31/8 (0.125) ist 3 Halbierungen von 1 entfernt.
4.5.5.2 Simulieren wir eine Binomialverteilung
Die Binomialverteilung lässt sich gut als “Münzwurf-Verteilung” auffassen.
Werfen wir eine Münze und sehen wir, was passiert.
Mit sample() ziehen wir eine Stichprobe aus dem Ereignisraum x, hier 0 und 1. Dabei vereinbaren wir (willkürlich), dass 0 für “Kopf” steht und 1 für “Zahl”. size = 1 bedeutet, wir werfen die Münze ein Mal (d.h. Stichprobengröße size ist 1).
Okay, noch an Bord? Dann werfen wir die Münze 10 Mal:
replace = TRUE heißt, wir legen die Münze wieder zurück auf den Tisch, wenn wir sie geworfen haben. Oder anders ausgedrückt: Ziehen mit Zurücklegen.
R, mach dich bereit, wirf die Münze 1000 (1e3) Mal15:
Mit sum() nach dem Pfeifensymbol %>% haben wir aus dem Vektor muenze_oft, der aus der ersten Zeile resultiert, die Summe ausgerechnet.
Jetzt wissen wir, wie oft die Münze “Zahl” gezeigt hat, nämlich 515 Mal.
Wenn Sie einen Zufallsversuch wiederholen, muss nicht jedes Mal das gleiche Ergebnis resultieren. Entsprechend wird bei wiederholten Ausführung der Funktion sample() nicht immer das gleiche Ergebnis resultieren. Wundern Sie sich also nicht, wenn bei Ihrem Computer eine ähnliche, aber nicht gleiche, Zahl herauskommt.
Visualisieren wir mal unsere Münzwürfe. Dazu erstellen wir zuerst eine geeignete Tabelle, Tabelle 4.5.
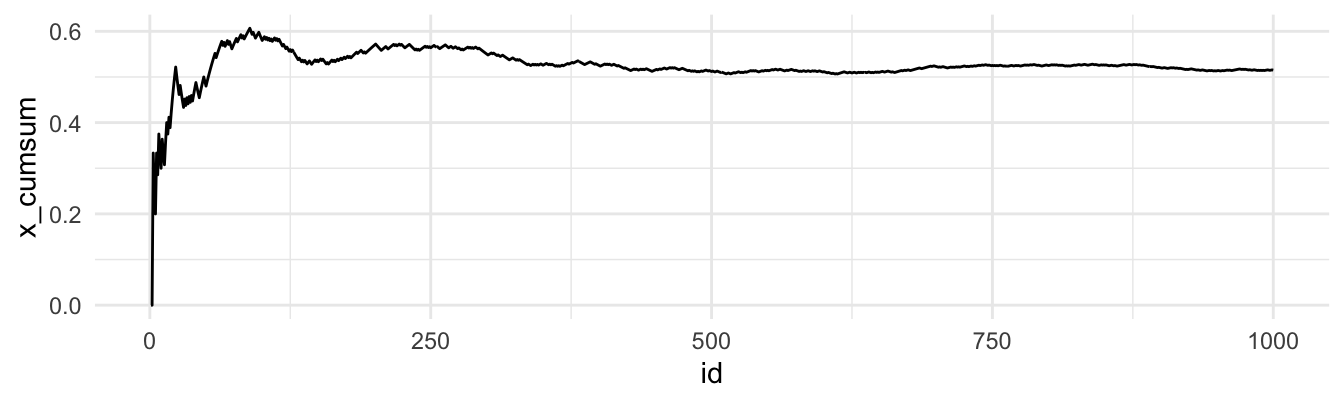
Und hier der Anteil von “Zahl” im Verlauf unserer Münzwürfe, s. Abbildung 4.23.16
Grob gesagt scheint sich ein Münzwurf nach, naja, vielleicht 500 Würfen “einigermaßen” zu stabilisieren.17
Zieht man (zufällig) immer mehr Werte aus einer Verteilung (mit endlichem Mittelwert), nähert sich der Mittelwert der Stichprobe immer mehr mit dem Mittelwert (oft als Erwartungswert bezeichnet) der Verteilung an.
4.6 Normalverteilung
4.6.1 Grundlagen
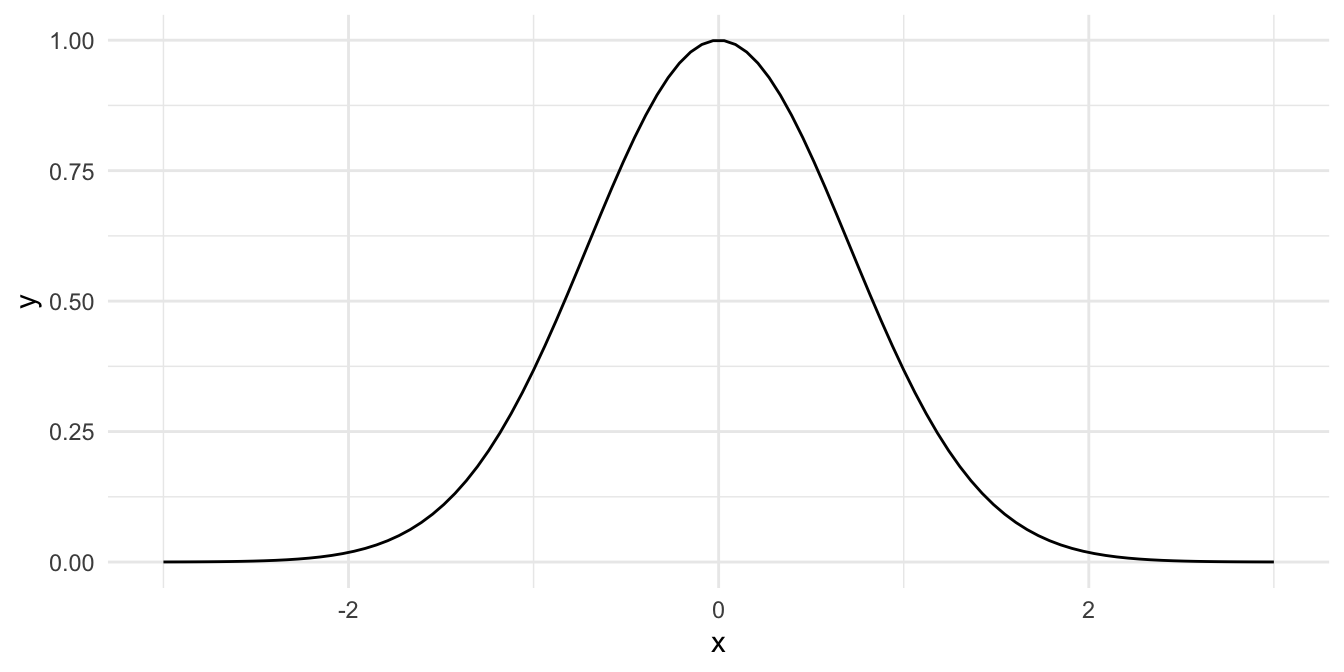
Definition 4.12 (Normalverteilung) Normalverteilungen haben eine charakteristische Glockenform; sie sind symmetrisch18. Normalverteilungen können sich unterscheiden in ihrem Mittelwert
Eine normalverteilte Zufallsvariable
Definition 4.13 (Parameter) Ein Parameter (einer Verteilung) legt die “Varianten” einer Verteilung fest. Durch die Wahl der Parameterwerte nimmt eine Verteilung eine genaue Form an.

Beispiel: Wie groß sind Studentis (Quelle des Datensatzes)?
Das Quantil von z.B. 25% zeigt die Körpergröße der 25% kleinsten Studentis an, analog für 50%, 75%, vgl. Tabelle 4.6.
Abbildung 4.25 zeigt eine Visualisierung der Quantile.
Das 25%-Quantil nennt man 1. Quartil, das 50%-Quantil auch 2. Quartil, das 75%-Quantil das 3. Quartil, und das 100%-Quantil (Maximalwert) das 4. Quartil.
Verwechseln Sie die Normalverteilung nicht mit der Paranormalverteilung, s. Abbildung 4.26.
4.6.2 IQ-Verteilung
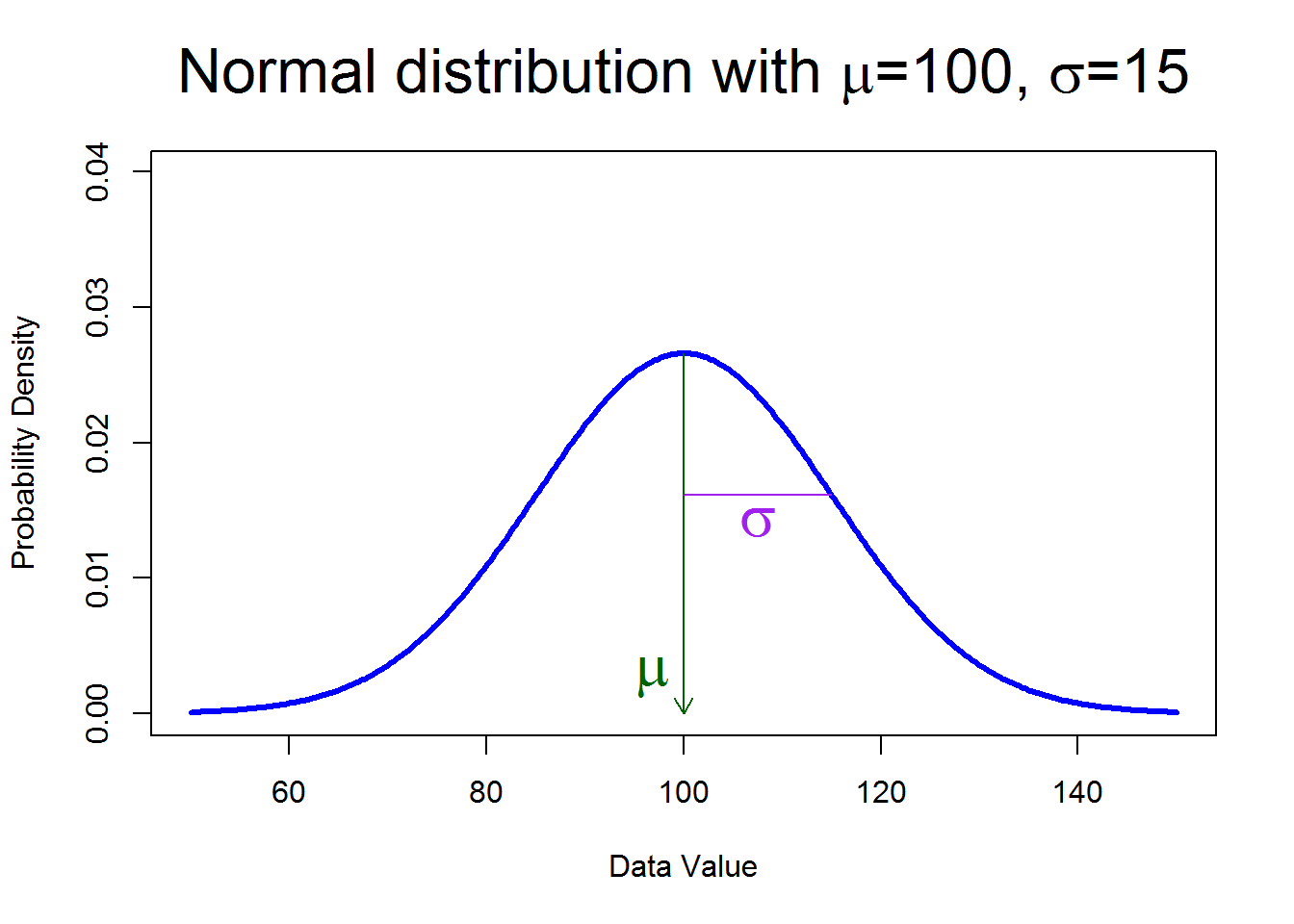
Die Verteilung der Zufallsvariablen IQ ist normalverteilt mit einem Mittelwert von 100 und einer Streuung von 15, s. Abbildung 4.27:
Übungsaufgabe 4.3 (Wie schlau muss man (nicht) sein?)
- Wie schlau muss man sein, um zu den unteren 75%, 50%, 25%, 5%, 1% zu gehören?
- Anders gesagt: Welcher IQ-Wert wird von 75%, 50%, … der Leute nicht überschritten?
Quelle:: John Kruschke.
Ziehen wir zufällig quantile(), s. Tabelle 4.7.
Das Quantil
Umgekehrt können wir uns auch fragen: Gegeben einer Realisation der Zufallsvariablen (z.B. IQ), was ist die zugehörige Wahrscheinlichkeit (Wert der Verteilungsfunktion?)
Übungsaufgabe 4.4 (Wie schlau muss man (nicht) sein, Teil 2)
- Welcher Anteil der Fläche unter der Kurve
- Anders gesagt: Welcher Anteil der Wahrscheinlichkeitsmasse der Verteilung liegt unter IQ=75, IQ=100, etc.?
Ziehen wir Stichproben aus iq < 100?
Tabelle 4.8 zeigt uns die Antwort.
Wir schätzen die wahre, “theoretische” Wahrscheinlichkeit durch einfaches Ausprobieren: Wir führen das Zufallsexperiment einfach häufig durch. Dann zählen wir den Anteil der Treffer. Nennt man auch “Simulieren”; klingt cooler als “Ausprobieren”.🤓
Anstelle von iq < 100 kann man iq < 115 einsetzen, etc.
Die Verteilungsfunktion (der Anteil der Wahrscheinlichkeitsmasse), p, für IQ-Werte nicht größer als 100,
4.6.3 Quantile der Normalverteilung
💡 Zur Erinnerung: Quantile teilen eine Verteilung so ein, dass ein Anteil
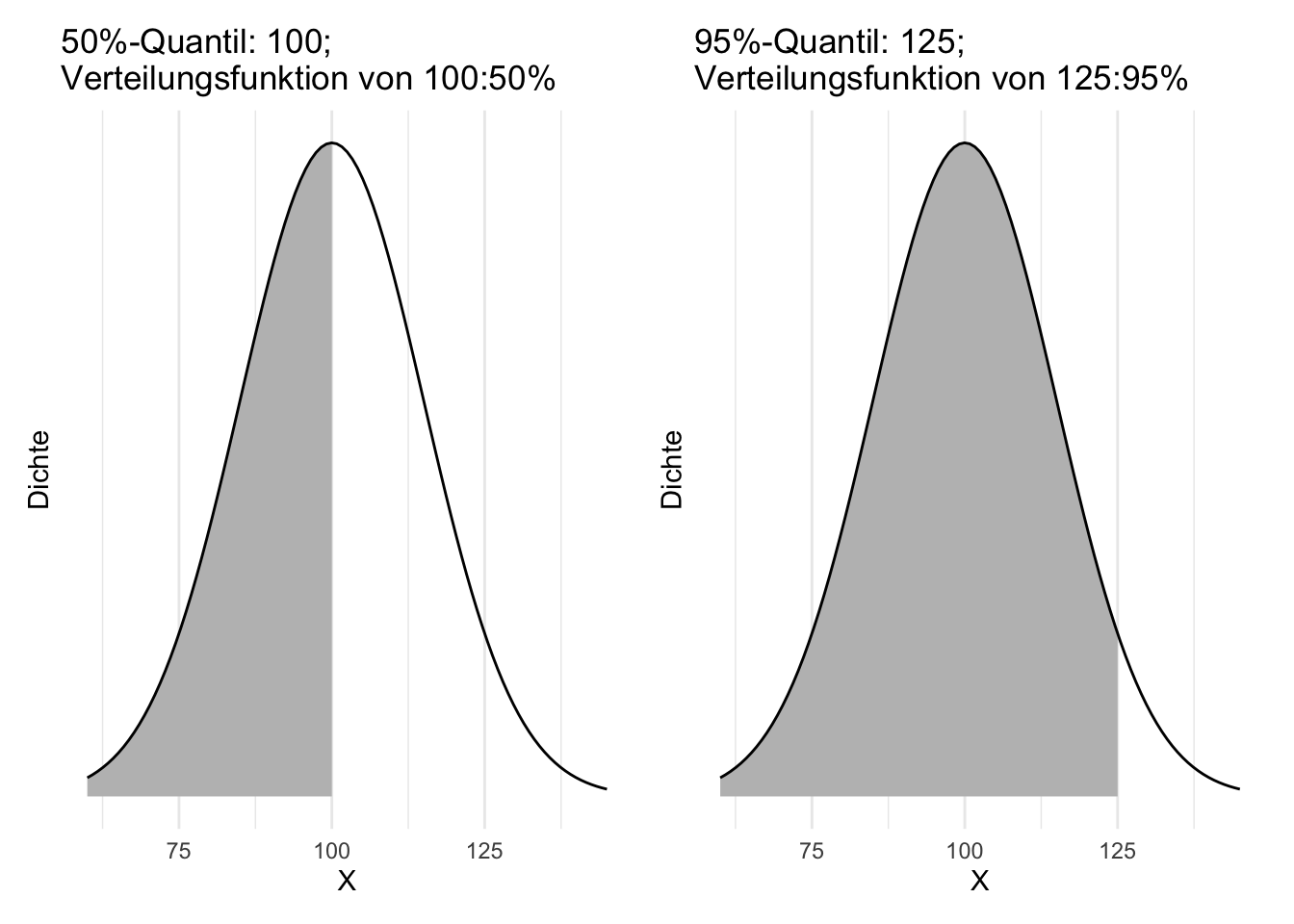
Beispiel 4.21 “50%-Quantil = 100” meint, dass 50% der Elemente der Verteilung einen Wert kleiner oder gleich als 100 haben. Man schreibt auch: q(.5) = 100.
💡 Zur Erinnerung: Die Verteilungsfunktion F (für einen Wert
Beispiel 4.22 “F(100) = 50%” meint: Die Wahrscheinlichkeit für eine Ausprägung von höchstens als 100 beträgt 50%.
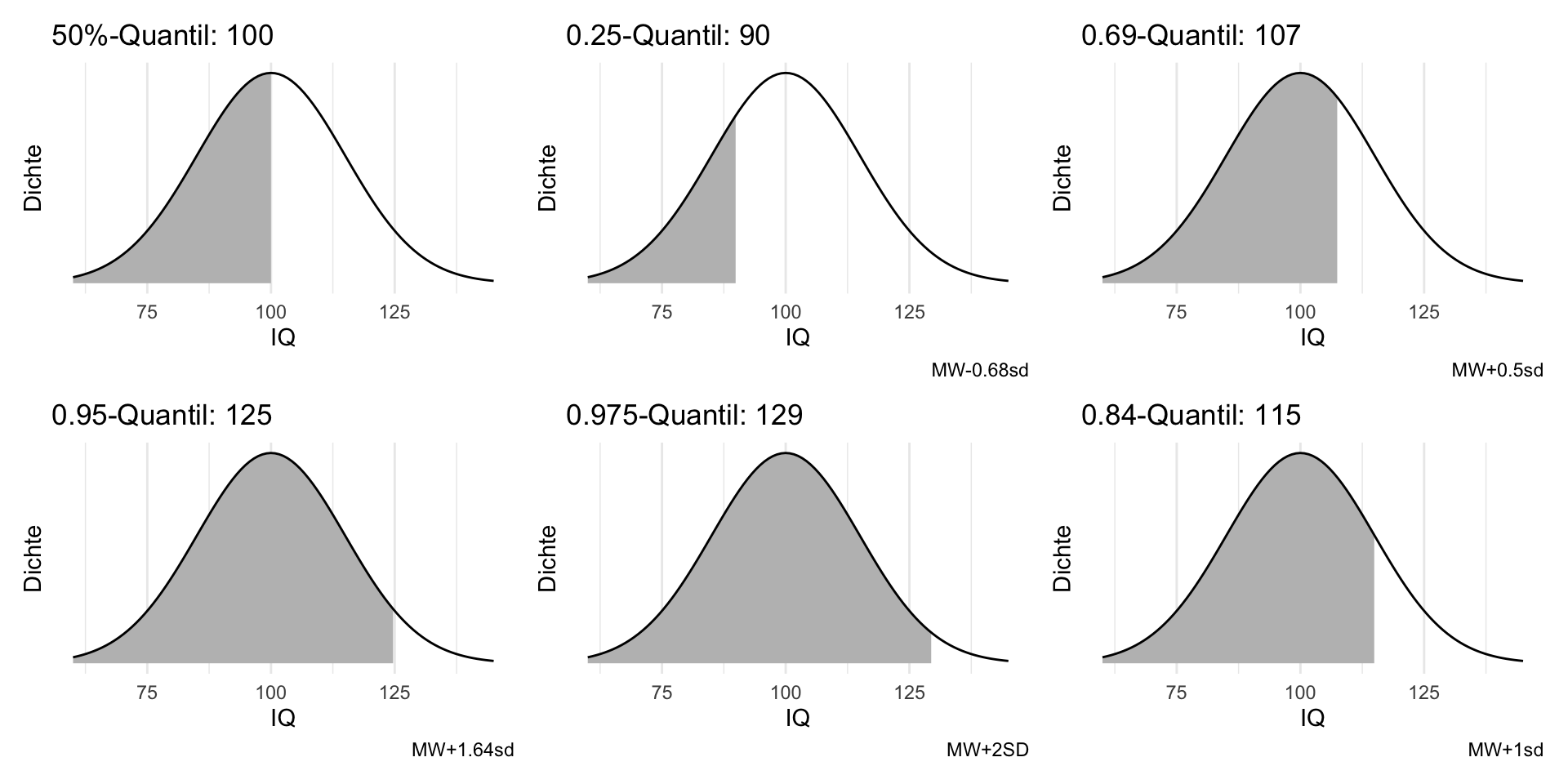
Schauen wir uns die Quantile der Normalverteilung einmal näher an. Wir gehen von einer Normalverteilung aus, wie sie zur Beschreibung von Intelligenz (IQ) verwendet wird, s. Abbildung 4.28.
Betrachten wir einige häufig verwendete Quantile für die IQ-Verteilung, s. Abbildung 4.29.
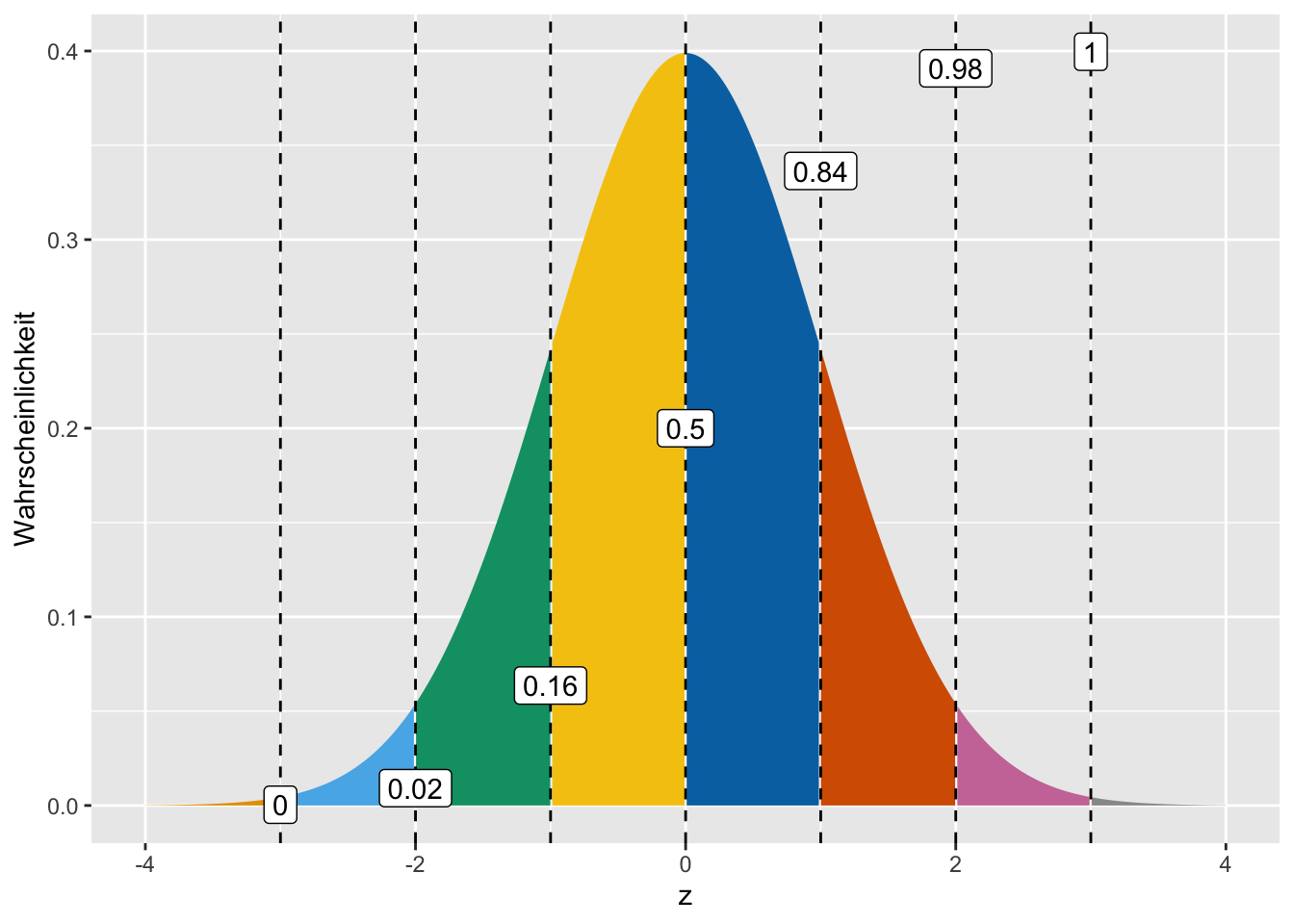
4.6.4 Standardnormalverteilung
Bei einer Standardnormalverteilung gilt, dass der Mittelwert 0 ist und die Standardabweichung 1, s. Theorem 4.5.
Theorem 4.5 (Standardnormalverteilung)
Bei
- hat eine Einheit von
- sind 50% der Wahrscheinlichkeitsmasse (Fläche unter der Kurve) kleiner als dieser Wert (Verteilungsfunktion).
In Summe liegen 100% der Wahrscheinlichkeitsmasse unter der Kurve.
Man kann jeder Normalverteilung in eine Standardnormalverteilung überführen mit der z-Transformation.
Ein z-Wert ist das Ergebnis einer z-Transformation, die definiert ist als der Abstand in SD-Einheiten,
den ein Wert vom Mittelwert entfernt ist, s. Theorem 4.6.
Theorem 4.6 (z-Transformation)
Tabelle 4.9 und Abbildung 4.31 zeigen wichtige Werte der Verteilungsfunktion für die Standardnormalverteilung.
4.6.5 Vertiefung
4.6.5.1 Normal auf dem Fußballfeld
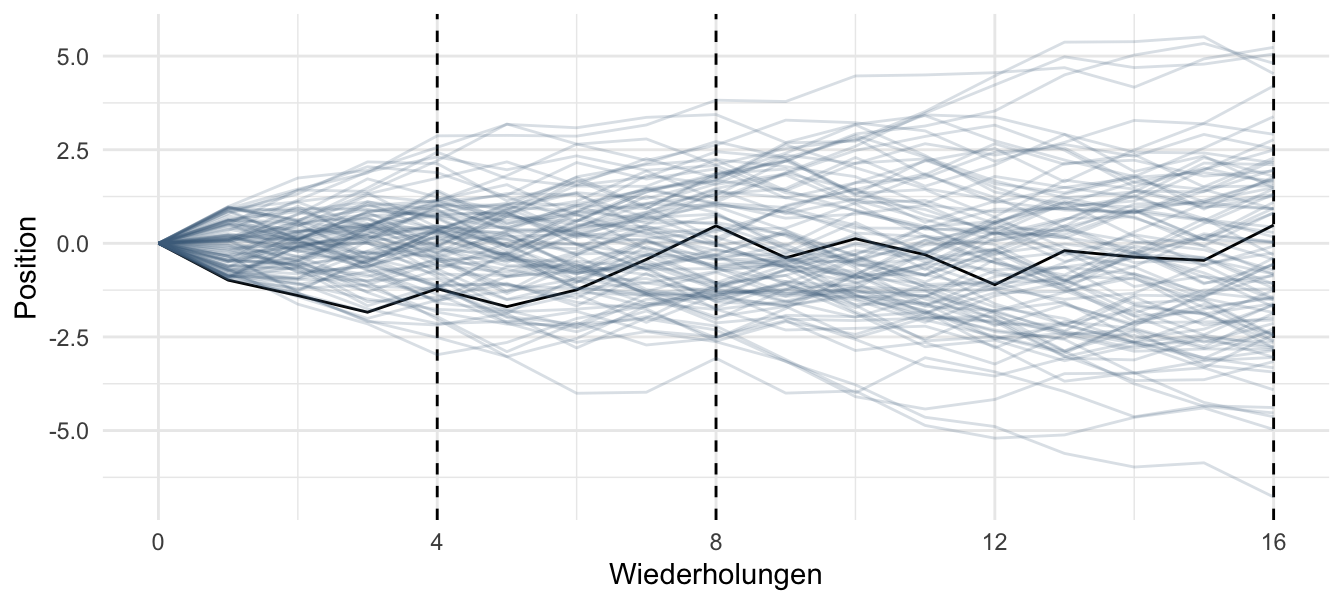
Sie und 100 Ihrer besten Freunde stehen auf der Mittellinie eines Fußballfelds. Auf Kommando werfen alle jeweils eine Münze; bei Kopf geht man einen Schritt nach links, bei Zahl nach rechts. Das wird 16 Mal wiederholt. Wie wird die Verteilung der Positionen wohl aussehen?
4.6.5.2 Normal durch Addieren
Die Summe vieler (gleich starker) Zufallswerte (aus der gleichen Verteilung) erzeugt eine Normalverteilung; egal aus welcher Verteilung die Zufallswerte kommen (Zentraler Grenzwertsatz), vgl. Abbildung 4.32.
4.6.5.3 Normalverteilung als konservative Wahl
Dem Mathematiker Carl Friedrich Gauss (s. Abbildung 4.33) wird die Ehre zuerkannt, die Normalverteilung eingeführt zu haben.
Quelle: Uni Greifswald, Public domain, via Wikimedia Commons
Ontologische Begründung
- Wirken viele, gleichstarke Einflüsse additiv zusammen, entsteht eine Normalverteilung (McElreath, 2020), Kap. 4.1.4.
Epistemologische Begründung
- Wenn wir nur wissen, dass eine Variable über einen endlichen Mittelwert und eine endliche Varianz verfügt und wir keine weiteren Annahmen treffen bzw. über kein weiteres Vorwissen verfügen, dann ist die Normalverteilung die plausibelste Verteilung (maximale Entropie) (McElreath, 2020), Kap. 7 und 10.
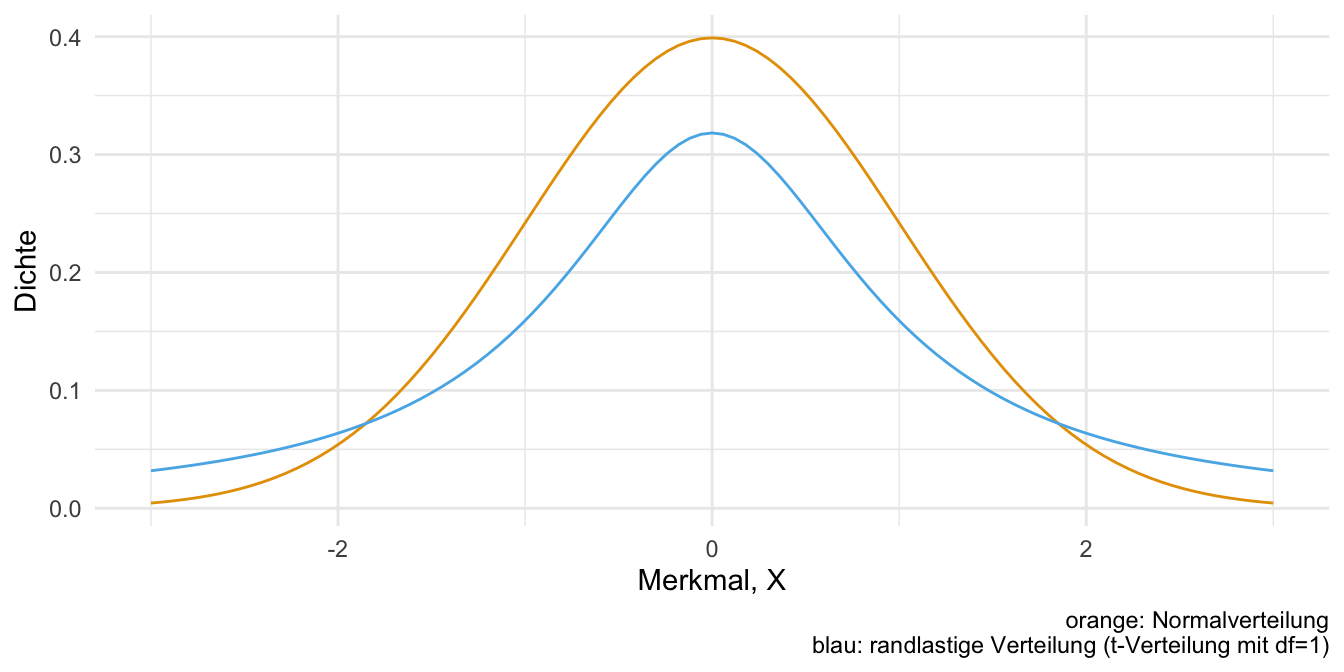
4.6.5.4 Normalverteilung vs. randlastige Verteilungen
Bei randlastigen Verteilungen (“fat tails”) kommen Extremereignisse viel häufiger vor als bei Normalverteilungen. Deshalb ist es wichtig sein, zu wissen, ob eine Normalverteilung oder eine randlastige Verteilung vorliegt. Viele statistische Methoden sind nicht zuverlässig bei (stark) randlastigen Methoden. Abbildung 4.34 grenzt eine Normalverteilung von einer “Fat-Tail-Verteilung” ab.
Beispiel 4.23 (Beispiele für Normal- und randlastige Verteilungen)
Normal verteilt:
- Größe
- Münzwürfe
- Gewicht
- IQ
- Blutdruck
- Ausschuss einer Maschine
Randlastig verteilt:
- Vermögen
- Verkaufte Bücher (Anzahl)
- Ruhm (z.B. Anzahl Follower auf Instagram)
- Aktienkurse (Kurswert)
- Erdbeben (Stärke)
- Anzahl von Todesopfern in Pandemien
- Anzahl von Todesopfern in Kriege
- Erfolg auf Tinder (Anzahl erfolgreicher Matches)
- Meteroritengröße (Volumen)
- Stadtgrößen (Einwohnerzahl)
4.6.5.5 Formel der Normalverteilung
Vereinfacht ausgedrückt lässt die Normalverteilung
mit
Wie man sieht (Abbildung 4.35) ergibt sich eine Normalverteilung.
Eine Normalverteilung mit
Die Normalverteilung wird auch Gauss-Verteilung oder Glockenkurve genannt.
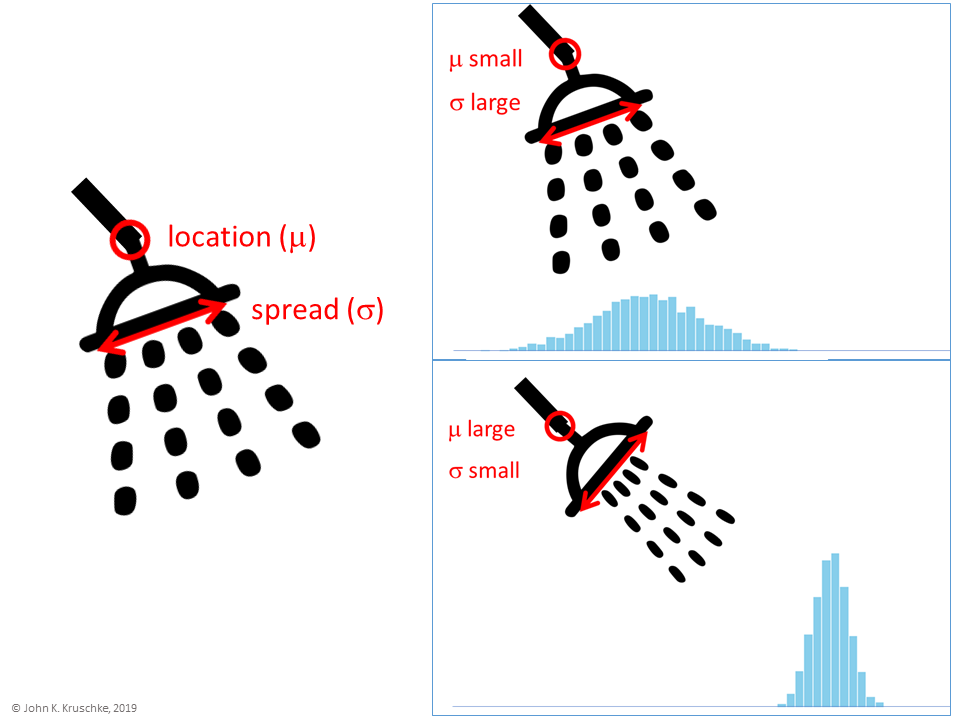
4.6.5.6 Simulation einer Normalverteilung
R hat eine Funktion eingebaut zur Erzeugung von Zufallszahlen (Zufallszahlengenerator), z.B. normalverteilte. Man übergibt dieser Funktion den gewünschten Mittelwert und die gewünschte Streuung und die Funktion zieht dann zufällig Werte aus dieser Verteilung.
Diesen Zufallszahlengenerator kann man mit einem Duschkopf vergleichen, s. Abbildung 4.36. An diesem Duschkopf kann man einen Schwenker einstellen, der den Duschkopf ausrichtet, also steuert, ob die Wassertropfen weit in die eine oder die andere Richtugn fallen. Zweitens hat unser Duschkopf noch einen Streuregler, der den Wasserstrahl entweder eng bündelt20 oder weit auseinanderfächert. Im ersten Fall fällt der Wasserstrahl eng und schmal aus. Im zweiten Fall fällt der Wasserstrahl breit aus.
Quelle: John Kruschke.
Eine Zufallszahl (random number), die normalverteilt ist, mit
Code
rnorm(n = 1, mean = 0, sd = 1)
## [1] 0.2664096Ein Fallbeispiel: Der Inhalt einer Tüte mit Zucker,
Wie groß ist die Wahrscheinlichkeit, dass 1000g unterschritten werden?
Simulieren wir uns 1e5 (100000) Zuckertüten!
id <int> | x <dbl> | |||
|---|---|---|---|---|
| 1 | 1002.479 | |||
| 2 | 1001.216 | |||
| 3 | 1003.320 | |||
| 4 | 1001.173 | |||
| 5 | 1001.465 |
Zählen wir, viele der Zuckertüten ein Gewicht von weniger als 1000g aufweisen:
Ein ziemlich21 kleiner Anteil. Rechnen wir uns noch die Anteile (proportion) aus:
4.7 Vertiefung
Bourier (2011), Kap. 6.2 und 7.1 erläutert einige (grundlegende) theoretische Hintergründe zu diskreten Zufallsvariablen und Wahrscheinlichkeitsverteilungen. Wichtigstes Exemplar für den Stoff dieses Kapitels ist dabei die Binomialverteilung.
Mittag & Schüller (2020) stellen in Kap. 12 und 13 Zufallsvariablen vor; zum Teil geht die Darstellung dort über die Lernziele bzw. Inhalte dieses Kurses hinaus.
4.8 Aufgaben
Zusätzlich zu den Aufgaben in der genannten Literatur sind folgende Aufgaben zu empfehlen.
4.8.1 Paper-Pencil-Aufgaben
4.8.2 Aufgaben, für die man einen Computer braucht
4.9 —

da einfach und deutlich↩︎
S wie Summe↩︎
Machen Sie das mal ohne Computer, wenn Sie ein Wochenende lang Langeweile haben.↩︎
Alternativ kann man z.B. auch
ggplotverwenden:ggplot(x_simu_df, aes(x = x_simu)) + geom_histogram(bins = 50).↩︎von lat. bis “zweimal”↩︎
Bei jeder Wiederholung des Zufallexperiments bleibt die Wahrscheinlichkeit der Ergebnisse gleich: Die Münze verändert sich nicht durch die Würfe (Ziehen mit Zurücklegen, ZmZ). Außerdem hat ein bestimmtes Ergebnis im ersten Wurf keinen Einfluss auf die Wahrscheinlichkeit eines bestimmten Ergebnisses im zweiten Wurf, etc., sog. “iid”: independent and identically distributed.↩︎
In den Lehrbüchern häufig als Urne bezeichnet, was den bösen Spott von “Friedhofstatistik” nach sich zog.↩︎
praktisch unendlich vielen↩︎
Da sehr viele Lose im Kästchen liegen, ist es praktisch egal, ob wir das Los wieder zurücklegen. Die Wahrscheinlichkeit für einen Treffer ändert sich (so gut wie) nicht.↩︎
Bei Taschenrechnern ist diese Funktion oft als “nCr” zu finden.↩︎
wobei “gering” subjektiv ist, die Betreiberfirma findet diese Wahrscheinlichkeit, dass 2 Pumpen ausfallen, wohl viel zu hoch.↩︎
wobei gelten muss
Hey, endlich mal was für echte Leben!↩︎
als “Logarithmus Dualis”, ld, bezeichnet↩︎
R meckert nicht bei langweiligen Aufgaben.↩︎
library(ggpubr); ggline(muenz_tab, x = "id", y = "x_cumsum")↩︎Was “einigermaßen” bedeuten soll, ist kein statistischer Begriff, sondern einer, der im echten Leben von den Menschen beantwortet werden muss, die eine Entscheidung zu treffen haben.↩︎
d.h. die Schiefe (
skewness) ist 0↩︎Das Zeichen
Massagedusche, behauptet der Hersteller↩︎
“Ziemlich” ist natürlich subjektiv; je nach Situation kann es zu viel oder nicht zu viel sein.↩︎